Built-in motion

From hierarchical architectures to complex composites, nature’s inventive use of geometry yields remarkable functionality from some rather unremarkable construction materials. This same control of geometry alongside a mastery of mechanics is used to transform elastic ‘failure’ into a crucial ingredient in the inner working of plants and organisms. Nature employs elastic instability so that large-scale motions can be triggered by the smallest and most specific stimuli. The Venus flytrap is perhaps the best-known example of this design philosophy — swelling induces an elastic instability that allows its leaves to snap between two stable configurations [1]. Using this snap-through behaviour, the plant moves quickly to capture its prey, allowing for the slow process of digestion to begin. Bacteria exhibit another beautiful example of this design paradigm, whereby their flagella, which are used to create thrust, buckle into a secondary configuration allowing the bacteria to control direction [2].

It is only recently that designers have started to use loss of structural stability in a similar manner. From merely being a mode of failure, buckling has become an increasingly well-trodden route to introducing novel functionality in the design of man-made structures and materials on many different length scales. This transition in perspective has been encapsulated as a move from ‘buckliphobia’ to ‘buckliphilia’ [3].

A powerful example of this paradigm is the use of buckling to turn simple geometries into mechanical machines: work in Physical Review Letters recently demonstrated that the buckling-unbuckling transitions in a hollow spherical shell can be used to create thrust in spherical swimmers [5]. It is well known that a spherical shell will buckle into a new geometry when the internal and external pressures are sufficiently different; as this deformation is elastic, the structure can return to its initial configuration when the pressure differential is removed. It was found that the asymmetry of geometries in the process of buckling and unbuckling allows for a net thrust to be created by cycling through these geometries while the structure is immersed in liquid.

Clearly, harnessing structural instability for a useful end has a parallel with the design principle observed in nature [3]. In some cases, however, there is deeper connection: the use of buckling as a control method for flow rates in a microfluidics device is a case where direct inspiration has been taken from nature, resulting in a functional man-made device. The giraffes’ long neck poses a unique problem in the control of blood flow to the animal’s brain. In order to maintain proper blood flow and pressure, both when the animal’s head is raised and lowered, the jugular vein collapses to restrict flow. This system was used as inspiration for a device that responds to a macroscale force input regulating fluid flow via elastic instability; such a system can be used to divert fluid from regions of low stress to regions of high stress [6].

Demanding materials applications require human ingenuity to go beyond the ordinary mechanical properties stemming for the molecular composition; we can now design structural responses that are imparted from the geometry of the building blocks in materials known as mechanical metamaterials. Symmetry breaking in the transition to the post-buckling regime and more generally, deformations that result from mechanical instabilities, can allows an extra degree of freedom for the designer: by programming a predetermined motion into the component parts, one can generate unprecedented mechanical properties including negative compressibility (meaning a material will get shorter under tension), negative Poisson’s ratio (or auxetic materials), and materials that under load exhibit pattern transformation or shape reconfiguration [4]. In the future, these material properties may be useful in designing mechanical sensors, auxetic fasteners, shock absorber, and actuators [4].

Built through buckling

The functionality of natural materials is significantly expanded by the adoption of buckling-driven morphing within an architecture. However, there is another equally profound way in which nature uses elastic instability that we are only beginning to use in man-made structures. In nature, buckling is also used as a fundamental ingredient in the fabrication of functional architectures.

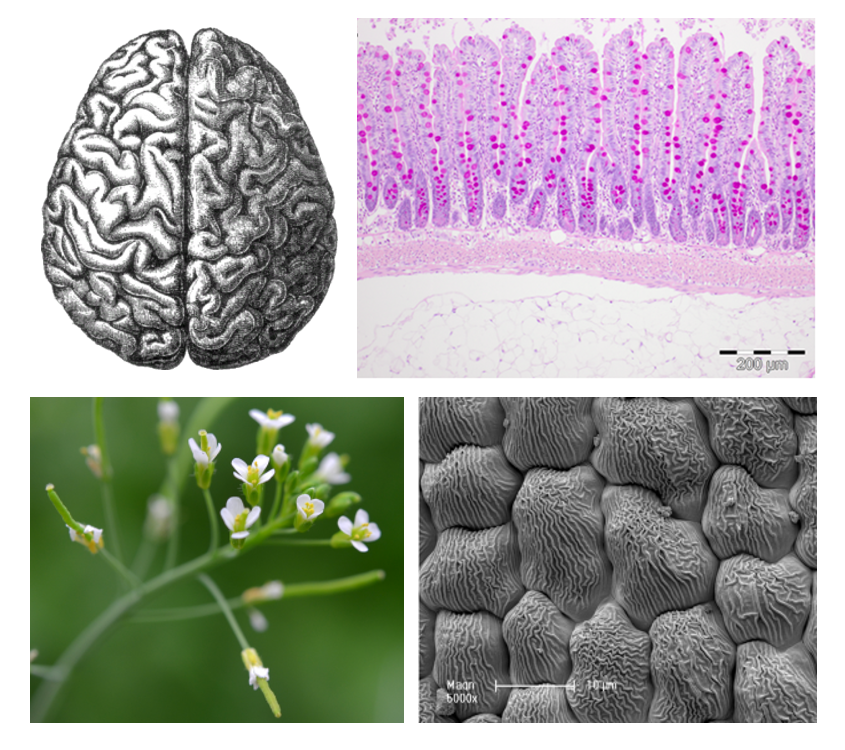
Two prime examples of this construction strategy come from within own bodies: elastic instability plays a fundamental role in the creation of the characteristic geometry observed on the surface of the human brain and gut [8, 9]. Both these architectures serve specialised functions within the body. The fold patterns in the brain are essential in fitting a large cortex in our skull, giving greater potential for information processing, while the increased surface area created by the architecture of the gut is important in the effective adsorption of nutrients. The appearance of the brain, with its convoluted pattern of sulci and gyri, and the small intestine wall with small finger-like villi are strikingly different in form and scale, however these architectures are generated in a similar fashion: a differential growth rate creates an energy landscape inducing buckling of the system, which in turn creates the desired geometry.

Other examples of this notion come from the plant world. Playing a major role in the attraction of pollinators to a plant, petals are of enormous importance to the sexual reproduction of higher plants. To aid the plant in this respect, the petals are generally rather striking in both form and colour, in some cases they even exhibit iridescence. It is now known that in many instances, these optical properties are not purely a result of pigmentation, but rather the petal has geometrically ordered patterns of cuticle on the petal epidermis creating diffraction gratings on the sub-micrometer length-scale. These diffraction grating manipulates light, endowing the petal with ‘structural colours’, permitting greater intensity and purity of colour than could be achieved through chemical means alone [7]. The fabrication method used by nature to create these ordered structures is rather ingenious: it is thought that differing rates of growth between the underlying epidermis and the rate of cuticle production causes buckling, reliably creating these highly specific geometries [7].

Creating complex architectures in the lab

Man-made structures utilising elastic instability as a route to complex architectures are fewer in number than their morphing counterparts, though they do exist. Buckling has recently been used as the driving force behind the creation of a self-assembled stretchable electronics device utilising micro and nanofibres. Using pre-strain as a critical ingredient in a fibre-substrate system, two-level wave-like geometries have been created where the substructure is a result of elastic instability; this use of instability makes the fabrication of the system much more straightforward than competing systems. This hierarchical, self-similar geometry allows for the creation of ultra-stretchable structures, with possible strain values of up to 250%. Systems of this nature have clear potential for applications in wearable electronics, novel sensors and bio-integrated devices [10].

A rather beautiful use of buckling as an integral part of the fabrication process is found in the patterning of 2D polymer surfaces [11]. One route to complex structures starts with the heating of a two-material system, in which the differing thermal properties of the materials create internal stresses, resulting in buckling. The buckled configuration is then used as a mold: material can be deposited by spin-coating in the micro-trenches, creating an intricate maze-like structure. To add extra functionality, a set of mechanical loads can then be applied to the sample, creating a second buckling pattern, allowing for another material to be deposited in the secondary buckled pattern. Using this methodology, a wide range of final multi-polymer geometries can be created [11].

Outlook

The authors are of the opinion that this second application of elastic instability, the use of buckling in the fabrication of novel geometries, is currently under-utilised. The scale independence of elasticity theory allows for similar processes to be used across different length-scales, potentially reducing problems related to the scaling down of components created in this manner. The flexibility of this methodology in fabricating a wide variety of geometries is in part demonstrated by the morphing examples, where buckled configurations of various geometries take on such a wide range of forms [4]. The importance of geometry in fields such adhesion, super-hydrophobicity, optics and structural optimisation cannot be underestimated; the use of elastic instability as a means to create novel, intricate geometries in a cheap, scalable manner has enormous potential to open new avenues for investigation.

References

[1] Y. Forterre, J. M. Skotheim, J. Dumais, and L. Mahadevan Nature 433, 421 (2005)
[2] K. Son, J. S. Guasto, and R. Stocker Nature Physics 9, 494 (2013)
[3] P. M. Reis, J. App. Mech. 82, 111001 (2015)
[4] K. Bertoldi, V. Vitelli, J. Christensen and M. van Hecke Nat. Rev. Mat. 2, 17066 (2017)
[5] A. Djellouli, P. Marmottant, H. Djeridi, C. Quilliet, and G. Coupier. Phys. Rev. Lett. 119, 224501 (2017)
[6] D. P. Holmes, B. Tavakol, G. Froehlicher and H. A. Stone, Soft Matter 9, 7049 (2013)
[7] R. L. Kourounioti et al., J. Royal Soc. Interface 10, 20120847 (2012)
[8] T. Tallinen et al., Nat. Phys. 12, 588 (2016)
[9] A. E. Shyer et al., Science 342, 212 (2013)
[10] J. Bian, Y. Ding, Y. Duan, X. Wan and YA Huang, Soft Matter, 13, 7244 (2017)
[11] D. C. Hyun et al., Adv. Mat. 22, 2642 (2010)