Adding only the right lines in energy networks
Published in Electrical & Electronic Engineering

Braess’ paradox upon upgrading networks
The increasing share of renewable energy sources causes electric power grids to be more distributed and decentralized as well as their dynamics to be more fluctuating, heterogeneous and unpredictable. Upgrading grids by adding transmission lines thus constitutes an essential step in securing robust electric energy supply in the future. Adding new lines to a network, such as to a power grid, is therefore generally thought of being beneficial for network functionality. However, as we demonstrate in our article [1], adding certain new lines may also decrease network performance -- establishing the emergence of "Braess' paradox" in large-scale power grids.
In 1969, Dietrich Braess, a mathematician at Ruhr University Bochum, Germany, first discussed the phenomenon for traffic networks: He found that opening up certain new roads may increase the average travel time for all [2] (translated into English in [3]). This effect has since been observed in real-world traffic systems, discussed for mechanical, biological and other systems. For electric power transmission grids, it has only been predicted theoretically [4].
Through a long-lasting interdisciplinary collaboration, we have now demonstrated that Braess' paradox may indeed emerge in real large-scale grids: From lab-scale grid experiments to detailed simulations of the German power grid, we consistently observed that adding certain lines or upgrading existing ones increases the strain on the grid and brings it closer to a failure. Intriguingly, although the phenomenon seems surprising at first, our theoretical findings moreover offer an intuitive explanation of why and via which lines Braess’ paradox may occur.
Why does Braess’ paradox emerge?
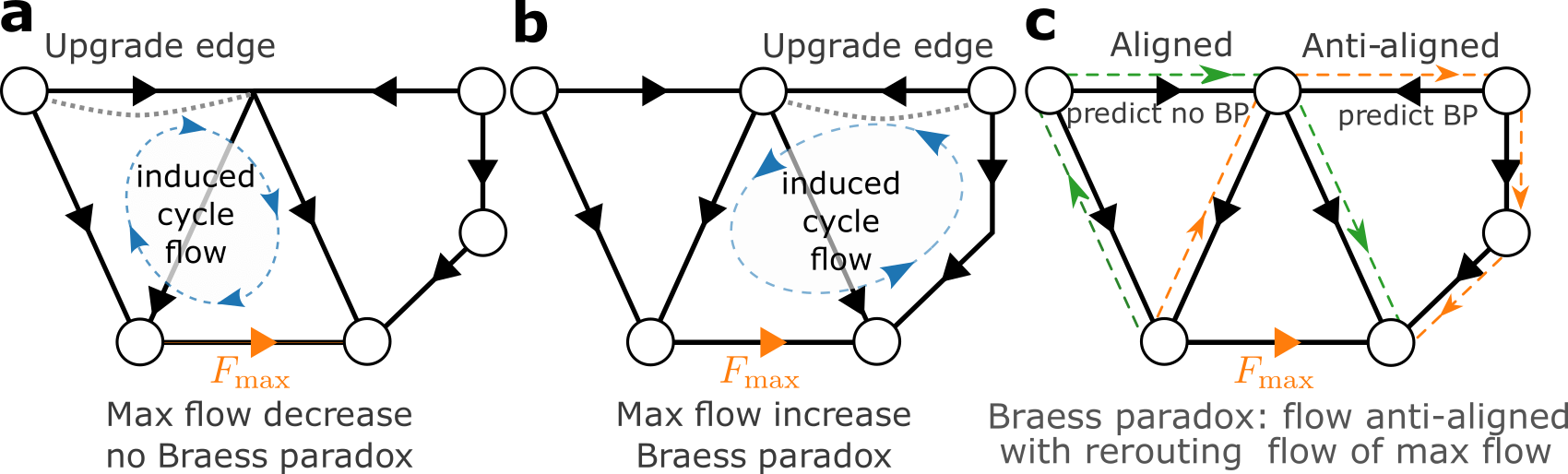
Suppose you upgrade one line (also called "edge") of a flow network, such as a power grid, for instance by reducing its resistance. The upgrade will allow additional flow along the upgraded line. If losses at the nodes are low, the total flow (e.g. electric power) originating from and directed towards a given node (e.g. a power consumer or generator) is fixed. So additional flow entering a node via one line will either cause that node to receive less flow via other lines or to transmit more flow away from it on these lines to balance total out-flow with in-flow. The figure below illustrates this consequence. Additional flow from node 2 into node 3 means that node 2 is sending less power to node 1 on the line (2,1) while node 3 transmits more power towards node 6 on line (3,6). Effectively, the line upgrade induces a cyclic flow. All these flow changes are uncritical as long as the maximum flow Fmax in the network does not increase (as in panel a). However, if the cycle flow aligns with the maximally loaded line and increases its flow, then effectively the line closest to failure in the entire network is brought even closer to an overloaded state and we observe Braess’ paradox (panel b). In the worst case, the line upgrade leads to an overload, a shutdown of the overloaded line and the whole network ceases to function properly.
In general, we reduce the problem of identifying Braess’ paradox to identifying additional flows as aligned or anti-aligned to the original flows (panel c).
From theory to experiment and large-scale grid extensions
We have been lucky to be able to test the theoretical hypotheses about the emergence of Braess’ Paradox in the lab and in large-scale simulations. How did we manage? Step one: Find some dedicated and friendly engineering colleagues willing to take a chance on lab-testing Braess’ Paradox based purely on theoretical prior insights [5].
We found such engineering collaborators at Clausthal University of Technology and the nearby Energieforschungszentrum Niedersachsen (EFZN) in Goslar. Step two: Plan the experiment in full detail to avoid damaging any equipment and assist throughout the measurements to resolve potential conceptual or experimental challenges (image: Benjamin Schäfer during one experiment at an EFZN lab). Step three: Find another brilliant engineer implementing a detailed full-scale grid simulation for Germany, faithful to technical constraints and including planned national line extensions. Step four: Assess Braess' paradox through both, experimental observations and the realistic grid simulations and combine the outcomes with the theory based on cyclic flows sketched above. These steps, jointly achieved through experimentation, data analysis, modeling, theory and simulation, enabled us to see the full picture and demonstrate the potential impact of Braess’ Paradox in large scale electric power systems.

Such a long-term interdisciplinary collaboration across electrical engineering, applied mathematics and physics and between theory and experiment is common for addressing many broader questions about the collective dynamics of complex systems. It was both, challenging and rewarding. The ways researchers from different backgrounds think, plan, communicate and write differ strongly between communities. We had several conversations about how to (and how not to) set up the experiments, how technical or how sketch-like a figure should be, how many details can be delegated to Methods or Supplementary Sections and even about which writing software to use. Simultaneously, tackling a complex systems’ problem thoroughly from experiment and data analysis to theory and simulation is highly motivating and inspiring. Our experience along the project also speaks of the precariousness of the academic system and the patience of all collaborators. We finished this project while Benjamin Schäfer changed his employer four times, switching among three countries, Marc Timme moved between cities and institutions, needing to drag with him and renew the grant that substantially funded our research, Dirk Witthaut received tenure and Hans-Peter Beck, a key engineering principal investigator, retired from his job at EFZN.
What are the results good for?
Fortunately, most power grids have sufficient spare capacity to withstand Braess' paradox and grid operators are diligently checking many potential scenarios before constructing new lines and during operation. Still, there are not always sufficient resources and time to consider every possible scenario and the sequence of upgrading different grid parts may change due to external, e.g. financial or political, factors. In all such cases, our intuitive understanding of how, under which conditions and at which lines Braess' paradox will emerge, may guide planning and operation decisions to make the electricity grids powered by renewables more robust and overall more future-compliant.
References
[1] Schäfer, B. Pesch, T., Manik, D. et al., “Understanding Braess’ Paradox in power grids”, Nature Communications 13, 5396 (2022). https://doi.org/10.1038/s41467-022-32917-6
[2] Braess, D. Über ein Paradoxon aus der Verkehrsplanung. Unternehmensforschung Operations Research 12, 258–268 (1968). https://doi.org/10.1007/BF01918335
[3] Braess, D., Nagurney, A. and Wakolbinger, T. "On a paradox of traffic planning", Transportation Science 39.4: 446-450 (2005). https://doi.org/10.1287/trsc.1050.0127
[4] Witthaut, D. and Timme, M., “Braess's paradox in oscillator networks, desynchronization and power outage”, New Journal of Physics 14(8):083036 (2012). https://doi.org/10.1088/1367-2630/14/8/083036
[5] Manik, D., Witthaut, D., and Timme, M., “Predicting Braess' Paradox in Supply and Transport Networks”, arXiv:2205.14685 (2022). https://doi.org/10.48550/arXiv.2205.14685
Follow the Topic
-
Nature Communications

An open access, multidisciplinary journal dedicated to publishing high-quality research in all areas of the biological, health, physical, chemical and Earth sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Women's Health
Publishing Model: Hybrid
Deadline: Ongoing
Advances in neurodegenerative diseases
Publishing Model: Hybrid
Deadline: Mar 24, 2026



Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in