Graphene, a two-dimensional sheet of carbon atoms with a honeycomb lattice structure, has become a subject of immense interest for almost two decades due to its two-dimensional nature and novel mechanical, optical, and electrical properties. It is also an extremely promising enabling material for passive spin components with one major caveat. Spin-orbit coupling (SOC), a relativistic phenomenon that couples the spin of an electron spin with its momentum, is one method for realizing active spin-based devices. However, graphene, in its native form, lacks a strong SOC. Several methods have been proposed to enhance SOC in graphene, e.g., by adding hydrogen or fluorene atoms, decorating with heavy adatoms or different substrates, and so on. While these techniques work, they also degrade the intrinsic electronic properties of graphene. An alternate route is to couple graphene with materials having large SOC. An exciting family of recently discovered 2D crystals, transition-metal dichalcogenides (TMDCs), which are being used as substrates for graphene, can serve just this purpose. Unlike graphene, the atomic SOCs in TMDCs can be very strong due to the heavy transition metal atoms.

Before plunging into the complex graphene/TMDC heterostructures and considering their potential applications, it is imperative to understand the impact of the proximity of a TMDC on the electronic properties of graphene. A prominent aim is to understand the microscopic source of the proximity-induced SOC in single-layer graphene. The SOC for graphene heterostructures has primarily three components:

(1) a Kane-Mele term, which couples the spin, valley, and sublattice components and opens a topological gap at the Dirac point, (2) a Rashba term, which couples the spin and sublattice components; and, most importantly, (3) an Ising or Valley-Zeeman SOC, a particular type of SOC coming into play from the proximity of TMDCs, which couples the spin and valley degrees of freedom [1]. In the presence of a strong Ising SOC, the electronic band dispersion of graphene is predicted to be spin-split. Despite many exciting consequences, a quantitative study of the effect of a strong SOC on the electronic energy band dispersion of graphene has been lacking.

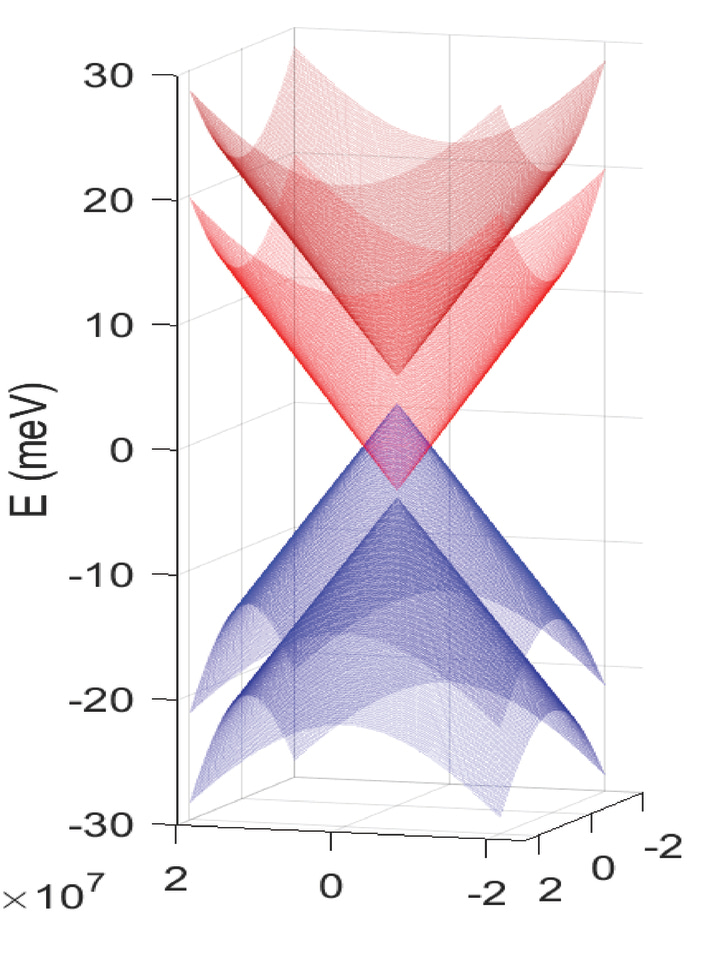
This work studies quantum oscillations in high-mobility graphene and trilayer WSe2 heterostructures. These heterostructures, encapsulated by hexagonal boron nitrate (hBN) of thickness ∼ 20 − 30 nm, are fabricated using the dry transfer technique (Fig. 1 (a)). Electrical transport measurements were performed in the low-energy range in a dilution refrigerator at the base temperature of 20 mK. In the presence of a magnetic field B, specific properties of an electronic system, like resistivity, show oscillations as a function of 1/B. These oscillations, called Shubnikov-de Haas (SdH) oscillations, are measured (See Fig. 1 (b)). In addition to the expected decay of the amplitude of the oscillations with increasing 1/B, we observe the appearance of beating, implying the presence of two closely spaced frequencies which are then confirmed by the fast Fourier transform of the data (Fig. 1 (c)). The appearance of two closely spaced frequencies implies that for each value of the Fermi energy, there are two distinct values of Fermi momentum k_F. This is direct proof of the energy splitting present in graphene’s conduction and valence bands. Using a detailed analysis of the temperature-dependent SdH oscillations, we find that the dispersion relation is linear with a Fermi velocity v_F ∼ 1.29 ± 0.04 × 10⁶ m/s and spin-splitting energy of nearly 5 meV (Fig. 1 (d)).

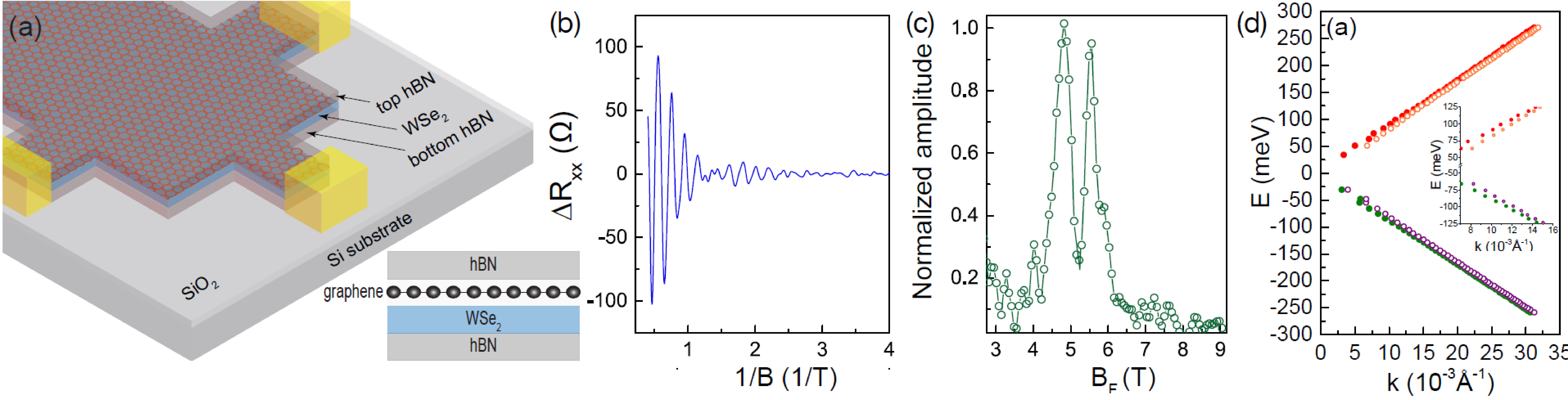
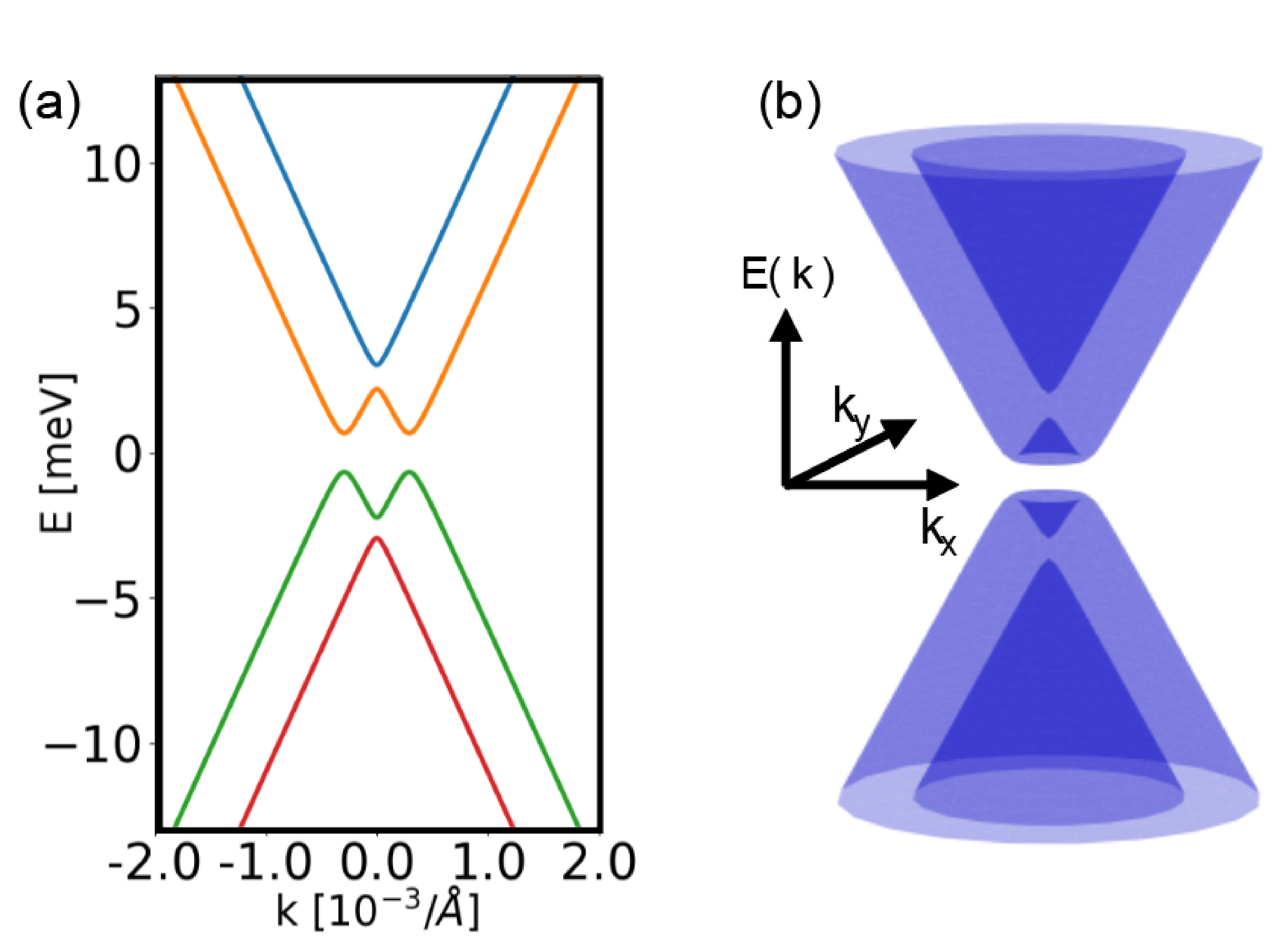
To better understand the spin-splitting energy dispersion, we fit a theoretical model to obtain the dispersion relation close to the Dirac point. This system has sublattice, spin, and valley degrees of freedom. The Hamiltonian has a term describing the linear dispersion of graphene near the Dirac points, a term representing a sublattice potential of strength ∆, and four possible spin-orbit couplings: (i) Kane-Mele SOC with strength λ_KM, (ii) valley-Zeeman SOC with strength λ_{V Z}, (iii) Rashba SOC with strength λ_R, and (iv) pseudo-spin asymmetric SOC with different strengths λ_{P IA} for the A and B sublattices of graphene. The experimental data are fitted to the Hamiltonian. We find that the best fit gives a Fermi velocity of 1.286 × 10⁶ ms⁻¹ in this sample which is about 1.5 times larger than that of pristine graphene. The parameters in the Hamiltonian which give the spin-split band gap in both conduction and valence bands are λ_{V Z} and λ_R. We find that the best fit gives the values of λ_{V Z} and λ_R to lie on a circle of radius 2.51 meV. This also implies a spin-split band gap of twice 2.51 meV, which matches the experimental data exceptionally well.

The relative magnitudes of λ_{V Z} and λ_R modify the dispersion of the lower energy band (E < 5 meV). Using the theoretically predicted value of λ_R = 0.56 meV yields the strength of the valley-Zeeman term to be λ_{V Z} = 2.45 meV and a maximum expected band gap of 3.3 meV. For these values of λ_R and λ_{V Z}, along with the theoretically estimated values of ∆ and λ_{P IA}, we obtain the expected energy dispersion for our model shown in Fig. 2.

Our work raises the possibility that in graphene with strong SOC, the transport properties near the Dirac point are dominated by charge carriers of a single spin component, making this system a potential platform for realizing spin-dependent transport phenomena, such as quantum spin-Hall and spin-Zeeman Hall effects.