SpringerLink

Numerical model for the identification of the convective heat transfer coefficient in cryogenic nitrogen cooling - Heat and Mass Transfer

Calculation of the convective heat transfer coefficient is challenging, especially for asymmetric boundary conditions, due to spatial variability. Numerical procedures are established methods to solve the parabolic heat equation. The solution describes the temperature distribution as a function of space and time under consideration of thermal boundary conditions. For asymmetric thermal boundary conditions the application of the one-dimensional heat equation in an algorithm to solve the inverse heat transfer problem is limited. The reasons are the neglected spatial effects. 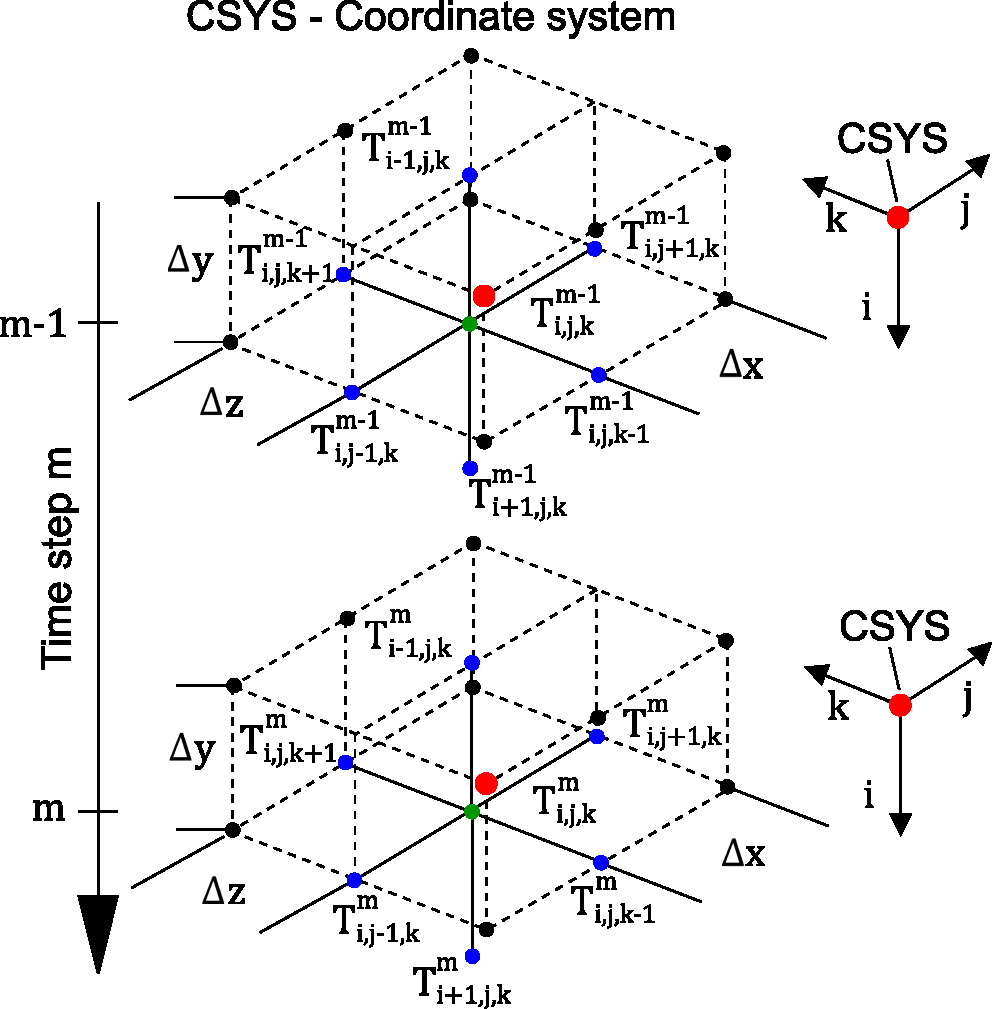The aim of this work is the development of a numerical method to calculate the convective heat transfer coefficient based on temperature measurements of a cooling process with liquid nitrogen, in two- and three-dimensional setup. The presented innovative algorithm is based on the tangent to the objective function, and is capable to calculate the correct order of magnitude of the convective heat transfer coefficient using finite difference and finite volume methods with a sensor concept that detects spatial heat conduction effects. The procedure was verified with experimental temperature measurements of a cooled cuboid made of non-alloy structural steel (S235). Different cooling methods were investigated, jet and immersion cooling with cryogenic nitrogen. The deviations of the calculated heat transfer coefficient for both numerical methods Finite-Difference and Finite-Volume-Method, compared to Finite-Element-Model reference data, are < 2%. The comparison with values obtained by empirical reference correlations (Asthakov and Breen-Westwater) show a maximum deviation of < 23% for jet cooling and < 10% for immersion cooling.