Introduction

The NV-diamond qubit platform provides a versatile tool for investigating quantum phenomena. It offers a multitude of well-controlled experimental degrees of freedom, making it a robust and tunable quantum simulator for studying complex and dynamic Hamiltonian models and properties that are otherwise challenging to explore. For example, researchers have used a single NV center to explore 2D synthetic quantum Hall physics [1], a topological phase transition of a quantum wire [2], and a synthetic monopole source in the Kalb-Ramond field [3].

Simulating topological invariants using qubits

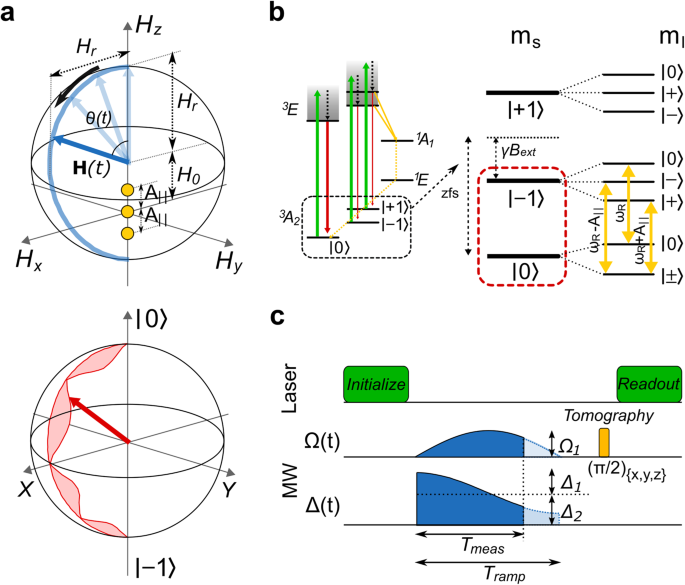
The Chern number is a topological invariant number, e.g., associated with the electronic band structure of materials. For a two-dimensional lattice system, points where two bands touch, such as the Dirac points located at the Brillouin zone, serve as sources of Berry flux in momentum space. The Chern number, obtained through integrating the Berry curvature over the Brillouin zone, exhibits a non-zero value when degeneracy points called Dirac points are present. In a two-level system, the degeneracy point analogous to the Dirac point is the resonance point, at which the length of the Bloch vector (representing the eigenvalue of the qubit Hamiltonian) becomes zero.

In 2012, Gritsev et al [4]. proposed a method for measuring the Chern number in a qubit platform. The approach involves evaluating the integral of the deviation of the qubit's Bloch vector from the trajectory of a time-varying Larmor vector on a hemispherical surface, which arises from a nonadiabatic response. Classically, the motion of a particle in a curved space deviates from a straight trajectory, and this curvature can be manifested through an effective force. An example of this is a charged particle moving in a magnetic field, which experiences a Lorentz force. Similarly, in the Hilbert space of a qubit, the Berry curvature can be observed by measuring the deviation of the qubit response as it follows the curved sweep path of a Larmor vector. Numerous qubit platforms have demonstrated Chern number transition measurements from 0 to 1 [5] and 0 to 2 [6], but not yet from 0 to 3, before our work.

Tunable Chern number up to 3

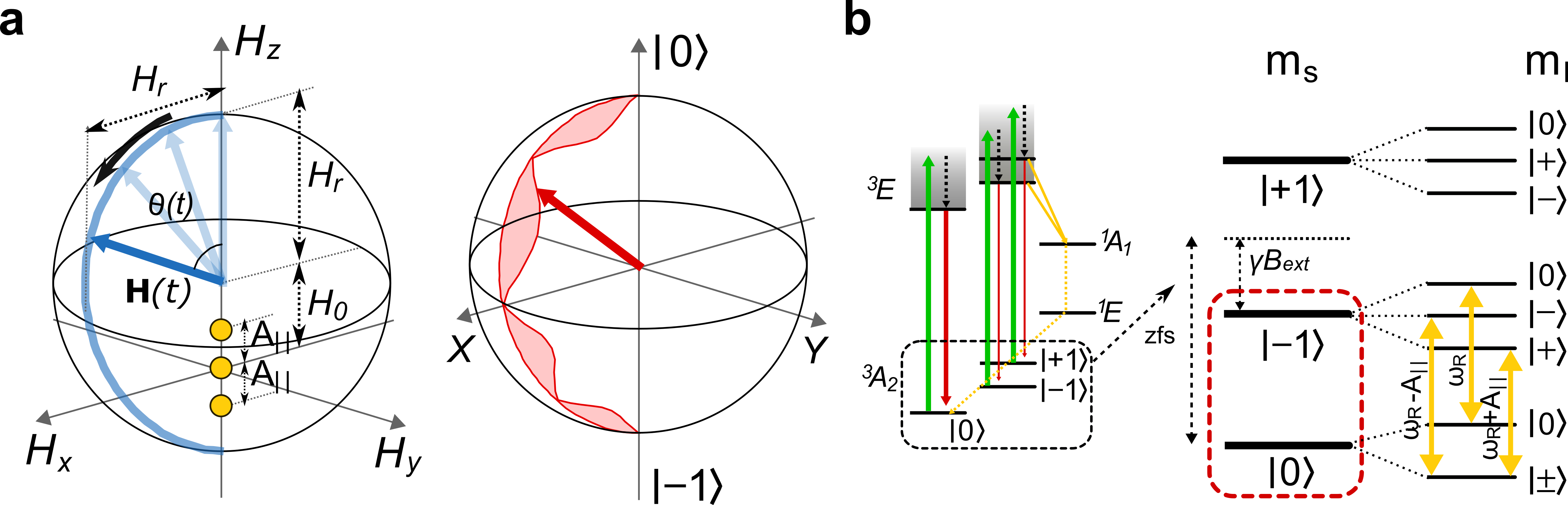
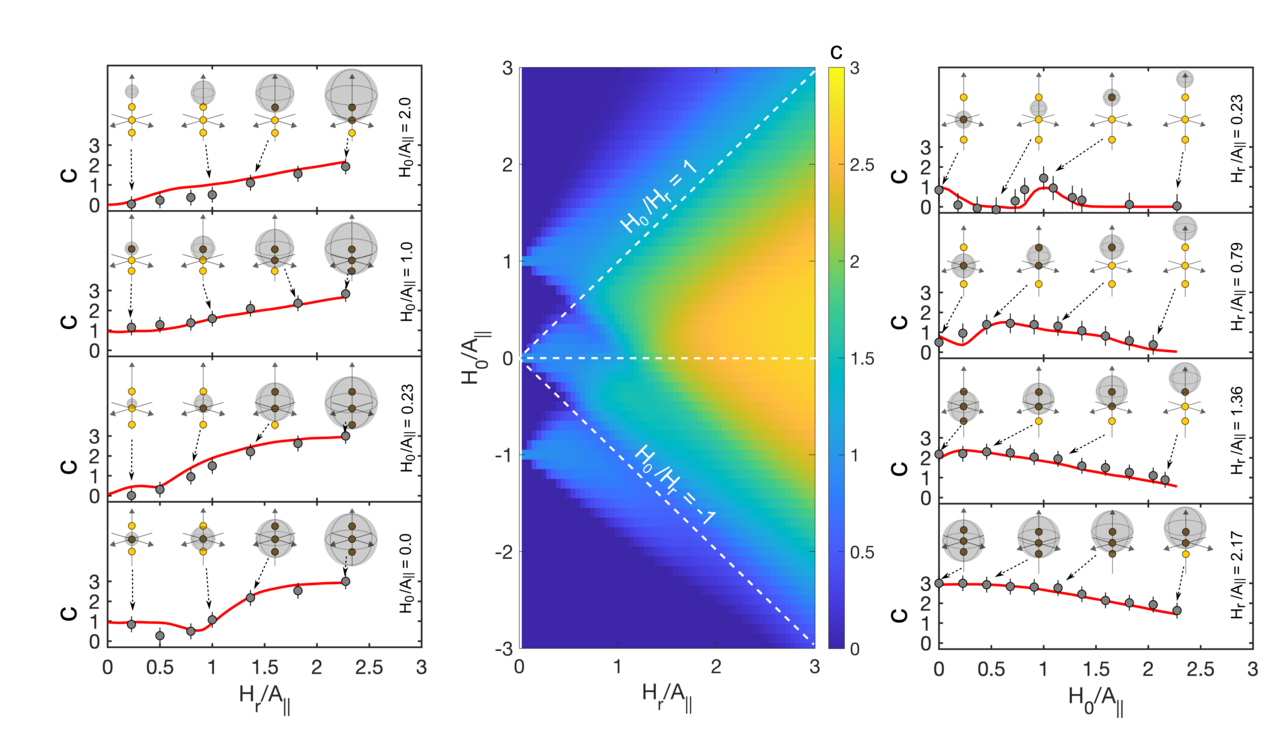
In the present work, we employ the Gritsev et al protocol to experimentally investigate the transition of the Chern number from 0 to 3. This is achieved by utilizing three degeneracy points corresponding to the ground-state spin energy levels of a single NV center in diamond (see Figure 1). The value of the Chern number is determined by the count of degeneracy points within the static internal Hamiltonian, which are enclosed by a control Hamiltonian sphere defined by the Larmor vector. Each degeneracy point can be interpreted as a synthetic magnetic monopole, generating radial synthetic magnetic fields that induce a torque on the Bloch vector.

By manipulating the geometric properties of the control Hamiltonian sphere, we systematically investigate the transition between different Chern numbers ranging from 0 to 3. This enables us to construct a two-dimensional topological phase transition diagram for a three-monopole Hamiltonian system.

Discussion and perspective

The investigation of higher Chern numbers and the study of transitions between different Chern numbers are of great interest in current research, relevant to both fundamental physics and practical technology. For instance, high Chern number phases observed in quantum anomalous Hall insulators have the potential to be utilized in low-power-consumption electronics, as the contact resistance between normal metal electrodes and chiral edge channels decreases with increasing Chern number [7-9].

Furthermore, the systematic design of the Hamiltonian parameter sphere in the present study unveils detailed topological structures involving three synthetic monopoles and highlights the intriguing Chern number physics associated with the adiabatic evolution of the system. This method can be extended to various qubit platforms to explore higher-dimensional topology, such as simulating the topology of non-interacting 2N band models [6] in condensed matter physics. Moreover, the tunability of the topological invariant in qubit systems opens up avenues for exploring more exotic forms of topology, thereby contributing to the field of topological quantum information science. 

References

[1]      Boyers, E., Crowley, P. J. D., Chandran, A. & Sushkov, A. O. Exploring 2D Synthetic Quantum Hall Physics with a Quasiperiodically Driven Qubit. Phys. Rev. Lett. 125, 160505 (2020).
[2]      Kong, F. et al. Direct measurement of topological numbers with spins in diamond. Phys. Rev. Lett. 117, 060503 (2016).
[3]      Chen, M. et al. A synthetic monopole source of Kalb-Ramond field in diamond. Science (80-. ). 375, 1017–1020 (2022).
[4]      Gritsev, V. & Polkovnikov, A. Dynamical quantum Hall effect in the parameter space. Proc. Natl. Acad. Sci. 109, 6457–6462 (2012).
[5]      Schroer, M. D. et al. Measuring a topological transition in an artificial spin-1/2 system. Phys. Rev. Lett. 113, 050402 (2014).
[6]      Roushan, P. et al. Observation of topological transitions in interacting quantum circuits. Nature 515, 241–244 (2014).
[7]      Chang, C.-Z. et al. Zero-Field Dissipationless Chiral Edge Transport and the Nature of Dissipation in the Quantum Anomalous Hall State. Phys. Rev. Lett. 115, 057206 (2015).
[8]      Wang, J., Lian, B., Zhang, H., Xu, Y. & Zhang, S.-C. Quantum Anomalous Hall Effect with Higher Plateaus. Phys. Rev. Lett. 111, 136801 (2013).
[9]      Fang, C., Gilbert, M. J. & Bernevig, B. A. Large-Chern-Number Quantum Anomalous Hall Effect in Thin-Film Topological Crystalline Insulators. Phys. Rev. Lett. 112, 046801 (2014).