Synaptic turnover is both stable and dynamic
Published in Neuroscience

The human brain excels at various tasks, even outperforming artificial neural networks in tasks that require flexibility and generalization. Interestingly, unlike artificial networks, the synapses in the brain are subject to continuous turnover, while our brain functions are fundamentally stable1. In contrast, artificial neural networks keep their synapses fixed after training, and making even minor connectivity adjustments can yield vastly different outcomes. This raises questions about how the brain balances ongoing synaptic change while safeguarding robustness and ensuring information retention despite the turnover of its synapses. What are the features of synaptic turnover that could help achieve functional stability?
In our paper, "Linking spontaneous and stimulated spine dynamics,"2 we studied this synaptic turnover and its properties. Synapses are the microscopic "communication bridges" in your brain, where neurons exchange electrical and chemical signals to transmit information, enabling everything from thought and memory to movement and emotion. An example of how the postsynaptic side of a synapse (also known as a spine) looks like on a neuron can be seen in the zoomed-in picture below.

When we get a learning cue (e.g., smelling a new smell or performing a new action), synapses connecting the relevant neurons are stimulated, resulting in changes in their features so that the next time this information needs to be processed, it is done faster and more efficiently, i.e., we have acquired a memory3,4. This concept is fundamental to Hebbian plasticity: "Cells that fire together wire together"5. What happens when no new memories need to be learned? Does the corresponding synapse remain constant? Well, the synapses, even in the absence of any trigger, change continuously… and this change can be quite significant. Just looking at one synapse in the microscope for approximately an hour, we can see that it grows and shrinks, thus changing the connection strength between the corresponding two neurons.1,6,7
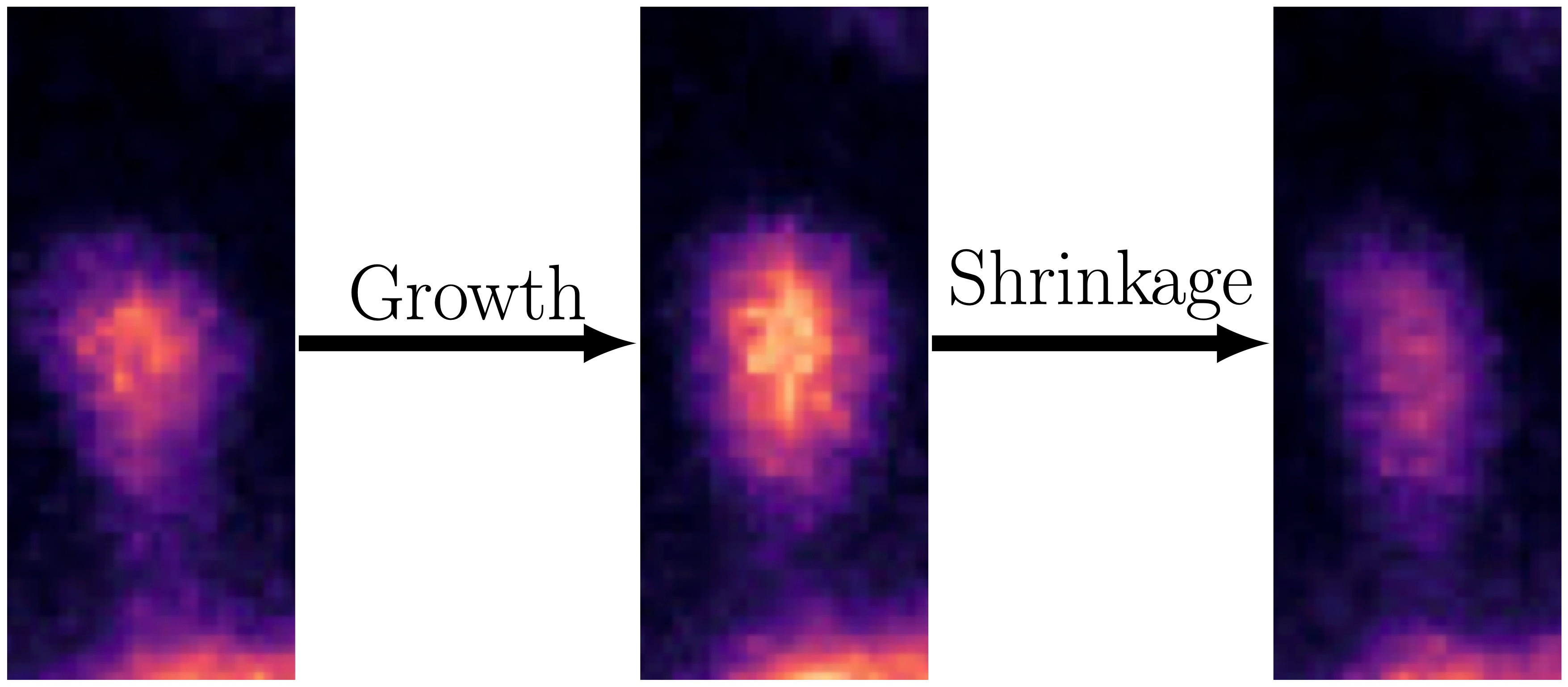
To better understand the difference between stimulation-triggered and spontaneous changes, we performed experiments where we studied synapses of a neuron (without providing any stimulus) for roughly an hour. After this period, we noted (and confirmed from previous studies1,6-8) some interesting observations.
-
Even though individual synapses were changing a lot, the properties of the full synaptic population remained constant.
-
If the synapse was big initially, it would be more likely to shrink in the next time frame, and vice versa; if it was small, it was more likely to grow.
-
Synapses also liked to counteract their previous random change, i.e., when a synapse grew at one point, it would be more likely to get smaller again. In the data, we corroborated this by showing a negative correlation between synaptic size changes from one time step to the next.
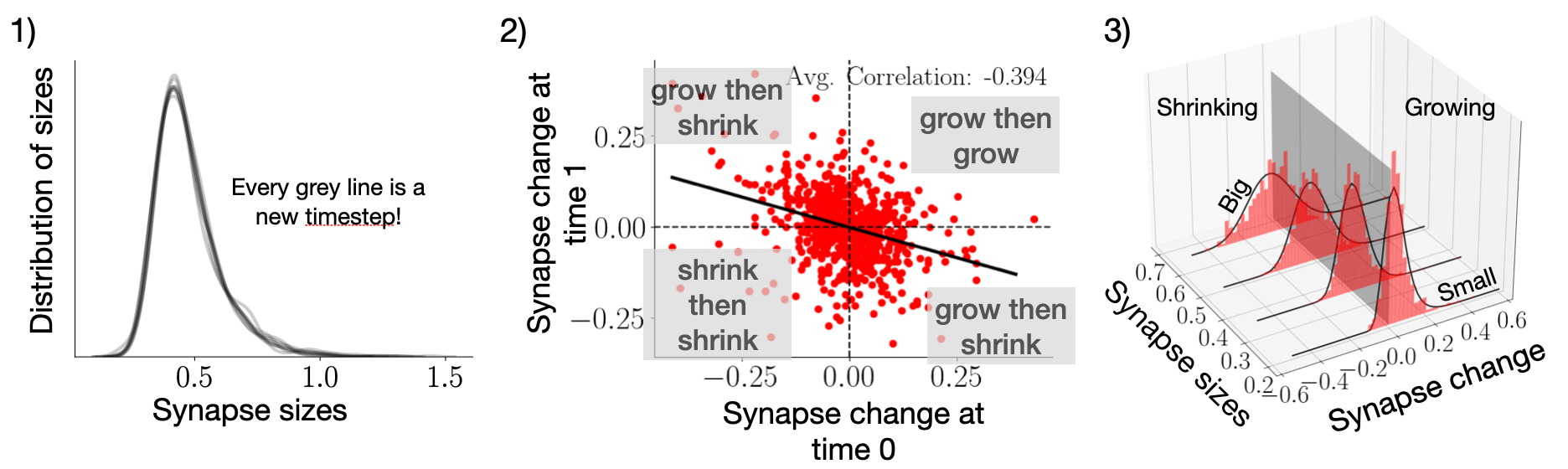
Using this information, we built a simple model that replicates the experimentally seen spontaneous behavior. For this, we needed three ingredients: Some randomness to mimic the biological diffusion of the proteins, some stability to ensure the synapses don't drift off to infinity or zero, and a component for the anti-correlation. This model, which is less detailed than molecular models used in other studies9-11, was able to recapitulate our dataset. However, the same three ingredients could also model the synaptic dynamics when a stimulus was present, i.e., when active learning occurred.
To study this "active learning," we performed a new set of experiments where some synapses were stimulated and observed that
- Only the small synapses grew substantially after the stimulus.
- The stimulation led to a significant shift in the network, giving it higher information-carrying qualities.
- However, the shift itself was very short (~2 minutes). After that, the spines as a population went back to their random, spontaneous activity.
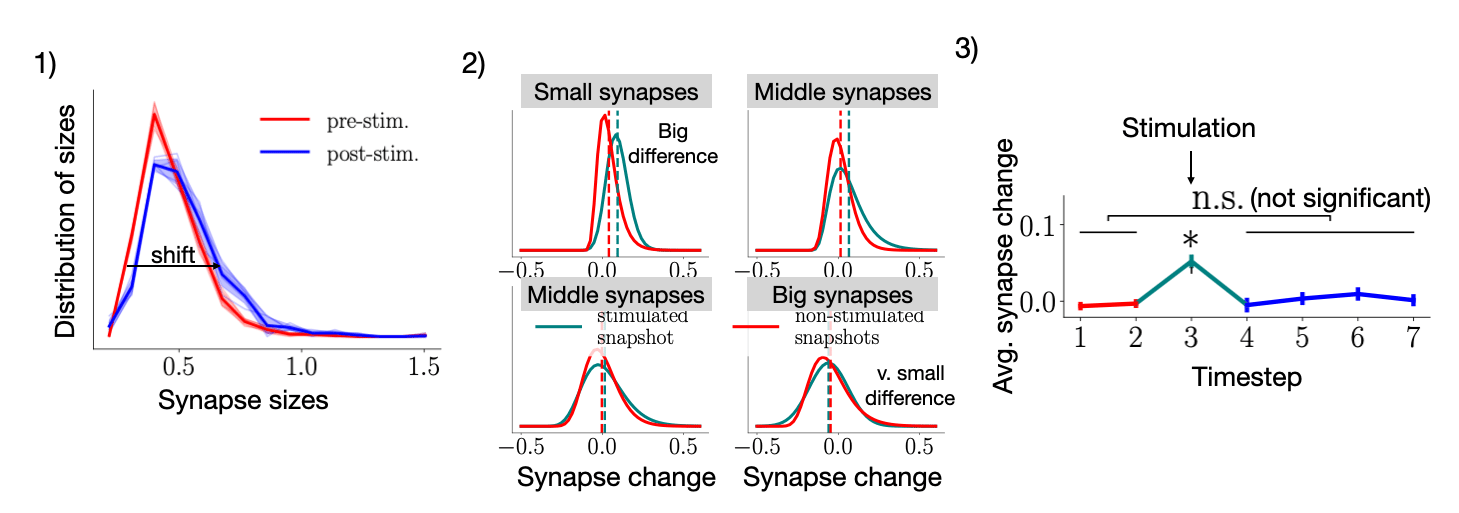
By applying our model to this scenario, we could see that our model's randomness and stability components were key to reproducing these phenomena. What does this imply? It implies that despite its apparent randomness, the spines' spontaneous activity uses the same mechanisms as stimulated synaptic activity. Maybe spontaneous activity can be seen as the other side of the memory coin: the one that degrades memories and skills we don't use so that the brain can efficiently learn new things. By taking advantage of the random biological processes, the brain may have found a cost-effective way of freeing up space.
References:
- Hazan, L. & Ziv, N. E. Activity dependent and independent determinants of synaptic size diversity. J. Neurosci. 40, 2828–2848 (2020).
- Eggl, M.F., Chater, T.E., Petkovic, J. et al. Linking spontaneous and stimulated spine dynamics. Commun Biol 6, 930 (2023).
- Stevens, C. F. & Sullivan, J. Synaptic plasticity. Curr. Biol. 8, R151–R153 (1998).
- Magee, J. C. & Grienberger, C. Synaptic plasticity forms and functions. Annu. Rev. Neurosci. 43, 95–117 (2020).
- Hebb, D. O. (2005). The organization of behavior: A neuropsychological theory. Psychology Press.
- Yasumatsu, N., Matsuzaki, M., Miyazaki, T., Noguchi, J. & Kasai, H. Principles of long-term dynamics of dendritic spines. J. Neurosci. 28, 13592–13608 (2008).
- Loewenstein, Y., Kuras, A. & Rumpel, S. Multiplicative dynamics underlie the emergence of the log-normal distribution of spine sizes in the neocortex in vivo. J. Neurosci. 31, 9481–9488 (2011).
- Ziv, N. E. & Fisher-Lavie, A. Presynaptic and postsynaptic scaffolds: dynamics fast and slow. Neuroscientist 20, 439–452 (2014).
- Shomar, A., Geyrhofer, L., Ziv, N. E. & Brenner, N. Cooperative stochastic binding and unbinding explain synaptic size dynamics and statistics. PLoS Comput. Biol. 13, e1005668 (2017).
- Bonilla-Quintana, M., Wörgötter, F., Tetzlaff, C. & Fauth, M. Modeling the shape of synaptic spines by their actin dynamics. Front. Synaptic Neurosci. 12, 9 (2020).
- Statman, A., Kaufman, M., Minerbi, A., Ziv, N. E. & Brenner, N. Synaptic size dynamics as an effectively stochastic process. PLoS Comput. Biol. 10, e1003846 (2014).
Follow the Topic
-
Communications Biology

An open access journal from Nature Portfolio publishing high-quality research, reviews and commentary in all areas of the biological sciences, representing significant advances and bringing new biological insight to a specialized area of research.
Your space to connect: The Psychedelics Hub
A new Communities’ space to connect, collaborate, and explore research on Psychotherapy, Clinical Psychology, and Neuroscience!
Continue reading announcementRelated Collections
With Collections, you can get published faster and increase your visibility.
From RNA Detection to Molecular Mechanisms
Publishing Model: Open Access
Deadline: May 05, 2026
Signalling Pathways of Innate Immunity
Publishing Model: Hybrid
Deadline: May 31, 2026




Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in