Our sense for numbers is imprecise, but efficiently so
Published in Social Sciences

Many of our decisions depend on some variables in our environment. We make these decisions, however, not directly on the basis of these variables, but rather on the basis of our internal representations of these external variables. In Plato's allegory of the cave, prisoners are forced to look at the shadows of real objects in the world, but they cannot see these objects directly. Socrates, perhaps, was smart enough to free himself from his chains, and come to understand the true nature of things; but the rest of us, prisoners of our brains, have to make do with the shadowy representations of the world afforded to us by our neurons. There is, however, a kind of information that we may seem to understand and to convey unequivocally: it is the case of numbers, through their most common symbolic representations, Arabic numerals. Indeed, the philosopher most anxious to be certain about something might find relief in the fact that the glyph “52”, for instance, imparts a piece of information that unambiguously corresponds to one precise number, and only to this one.
A sense for numbers

Several experiments, however, show that humans make mistakes in tasks involving Arabic numerals. Crucially, these mistakes are similar to the ones they make in psychophysics tasks involving physical stimuli. For instance, subjects fail more often at choosing quickly and correctly the greater of two digits when these two digits are close in value [1]. Together with neurobiological studies revealing the tuning curves of the neurons that encode for numbers in the human brain [2], these results suggest the existence of a “number sense” [3], i.e., a representational system for numbers very much like those existing for the features of physical stimuli (e.g., orientations of line segments).
Two important implications follow: First, one can study the human representations of numbers and hope to draw conclusions that could apply generally to the representations of many kinds of magnitudes in the human brain; and conversely, lessons learned about the representations of physical magnitudes may be relevant to our understanding of number representation. Second, if the “number sense” is like any other sense, then it is imprecise (“noisy”), and subject to biases. This has important consequences for the many decisions that humans make on the basis of numbers — including a great deal of economic decisions, which impact our daily lives, and also collectively matter for society as a whole. Thus we seek to understand the inner workings of human number representation, and to this end, we turn to the neuroscience of perception.
An imprecise but efficient brain
A popular idea in theoretical neuroscience is that the representations in the brain are imprecise because the brain's computational capacities are subject to constraints; but its representations are nonetheless efficient, i.e., they are optimal under these constraints [4,5]. This hypothesis, which has been called “efficient coding”, comes with the theoretical implications that the noise and the bias in an observer's estimates of presented magnitudes should verify two properties: (i) the bias and the noise should depend on the distribution of the presented magnitudes (the “prior”), and (ii) there should be a relation of proportionality between the bias and the derivative of the noise; this relation has been called a “law of human perception” [6,7]. The perception of orientations provides a concrete example of the first point: if people perceive vertical and horizontal orientations with less noise (higher precision) than oblique orientations, it is probably because the former are more frequent than the latter (at least in a database of natural images [8]). It makes intuitive sense, indeed, that more frequent stimuli be perceived more precisely.
This theory has gained traction in the past decade. It raises several questions. First, although it is supported by empirical results obtained with various physical stimuli, it remains unclear whether it applies to number representation, as suggested by the “number sense” theory. Second, if the prior distribution changes, over a short timescale, do the representations change, or are these only adapted once and for all to some long-run distribution?
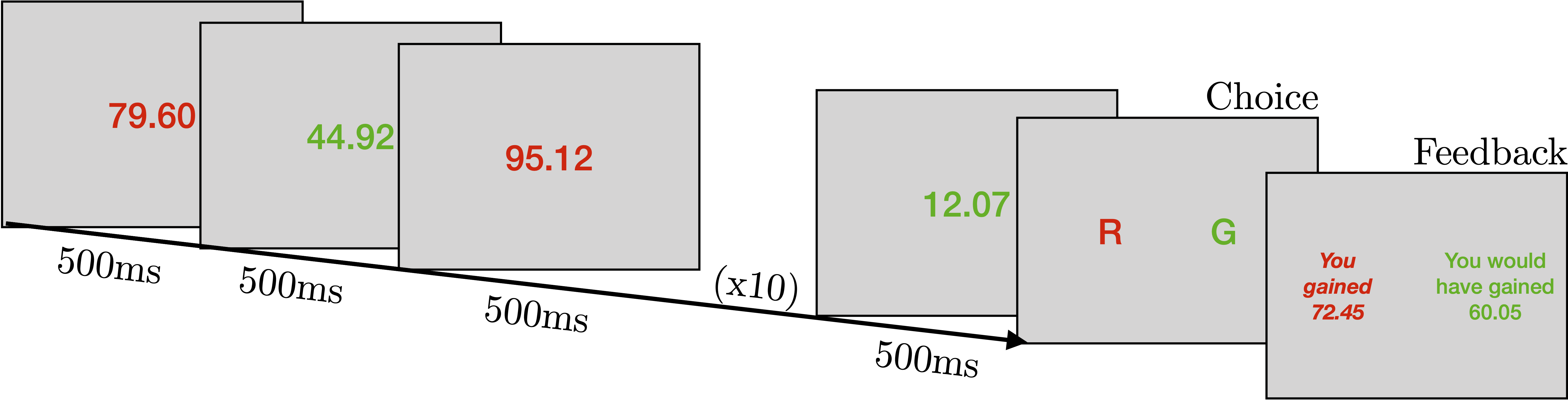
These questions are at the heart of our recent Nature Human Behaviour article. In this study, we design a task in which subjects are asked, at each trial, to decide which of two series of numbers have the higher average. We manipulate, across blocks of trials, the prior distribution, defined over a given range, from which these numbers are sampled: with the “Downward” prior, small numbers are more frequent; with the “Uniform” prior, all the numbers in the range are equally frequent; and with the “Upward” prior, large numbers are more frequent.
More frequent numbers are perceived with less noise
To analyze the choices of our subjects, we compare their responses to those of several models that are characterized by two features: whether or not the model subject estimates the presented number with a bias that depends on the value of the number, and whether or not the model subject estimates the number with a degree of noise (imprecision) that depends on the value of the number. We find that to satisfyingly reproduce subjects' data, the model subject must feature both a bias and a varying noise. Crucially, the noise varies with the value of the number in such a way that infrequent numbers are estimated with more noise. Thus with the Downward prior, large numbers are estimated with a high degree of noise, whereas with the Upward prior, it is the small numbers that are estimated with more noise.
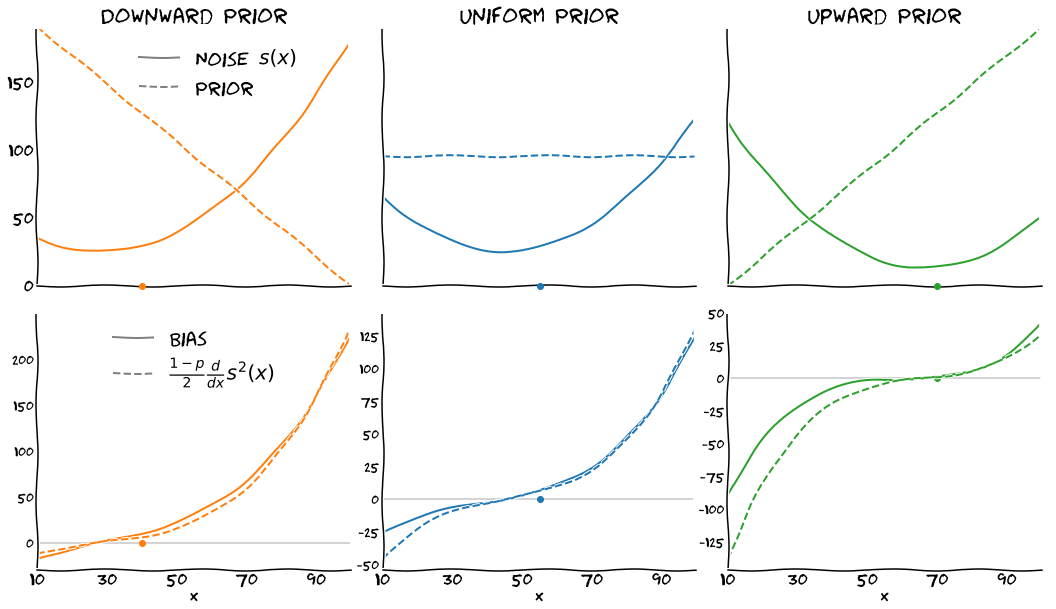
The fact that infrequent numbers are estimated in a more imprecise fashion suggests that subjects adapted their encoding to the prior distribution; and this in fact allowed them to optimize their expected reward in the task. Furthermore, we find that the subjects' bias is qualitatively consistent with a relation of proportionality between the bias and the derivative of the variance. In fact, by directly assuming this relation (which follows from principles of efficient coding) we obtain a parsimonious model of the behavior of subjects. (The article explains these things in greater detail.)
Conclusion
Our results show that the brain is able to adapt its representational apparatus for numbers, in order to efficiently take into account the frequency with which numbers are encountered. In short, more frequent numbers are perceived with more precision, and this can be modulated, within the one-hour duration of the experiment, if there is a change in the frequencies of the numbers. Our study provides theoretical and empirical support for the efficient-coding hypothesis, and extends its domain beyond physical magnitudes and to number cognition. Indeed, we show that efficient-coding models are not only relevant for the perception of physical stimuli, but also for the representation of the numerical meaning of a symbol — i.e., to the semantic content of a stimulus, instead of the magnitude of one of its physical attributes. It is tempting to extrapolate, and conjecture that such mechanism constitutes a “universal” scheme for the brain to represent any variable that can be understood as taking values on an ordered line: from the length of an object to the tastiness of a burger to the competence of a politician, etc. In the end, the true nature of things may escape us, but the true nature of our representations, perhaps, stands within our reach.
References
- Moyer, R. S., & Landauer, T. K. (1967). Time required for Judgements of Numerical Inequality. Nature, 215, 1519–1520.
- Kutter, E. F., Bostroem, J., Elger, C. E., Mormann, F., & Nieder, A. (2018). Single Neurons in the Human Brain Encode Numbers. Neuron, 100(3), 753-761.e4. https://doi.org/10.1016/j.neuron.2018.08.036
- Dehaene, S. (1998). The Number Sense: How the Mind Creates Mathematics. The American Mathematical Monthly, 105(10), 975. https://doi.org/10.2307/2589308
- Barlow, H. B. (1961). Possible Principles Underlying the Transformations of Sensory Messages. In W. A. Rosenblith (Ed.), Sensory Communication (pp. 217–234). The MIT Press. https://doi.org/10.7551/mitpress/9780262518420.003.0013
- Ganguli, D., & Simoncelli, E. P. (2014). Efficient Sensory Encoding and Bayesian Inference with Heterogeneous Neural Populations. Neural Computation, 26(10), 2103–2134. https://doi.org/10.1162/NECO_a_00638
- Wei, X.-X., & Stocker, A. A. (2017). Lawful relation between perceptual bias and discriminability. Proceedings of the National Academy of Sciences, 114(38), 10244–10249. https://doi.org/10.1073/pnas.1619153114
- Prat-Carrabin, A., & Woodford, M. (2021). Bias and variance of the Bayesian-mean decoder. In M. Ranzato, A. Beygelzimer, Y. Dauphin, P. S. Liang, & J. W. Vaughan (Eds.), Advances in Neural Information Processing Systems (Vol. 34, pp. 23793–23805). Curran Associates, Inc. https://proceedings.neurips.cc/paper/2021/file/c7c3e78e3c9d26cc1158a8735d548eaa-Paper.pdf
- Girshick, A. R., Landy, M. S., & Simoncelli, E. P. (2011). Cardinal rules: visual orientation perception reflects knowledge of environmental statistics. Nature Neuroscience, 14(7), 926–932. https://doi.org/10.1038/nn.2831
Prat-Carrabin, A., & Woodford, M. (2022). Efficient coding of numbers explains decision bias and noise. Nature Human Behaviour, 845–848. https://doi.org/10.1038/s41562-022-01352-4
Follow the Topic
-
Nature Human Behaviour

Drawing from a broad spectrum of social, biological, health, and physical science disciplines, this journal publishes research of outstanding significance into any aspect of individual or collective human behaviour.
Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in