https://www.academia.edu/143438760/FROM_PHI_TO_ALFA_ANGULAR_QUANTISATION_AND_MUSICAL_STRUCTURE_OF_THE_UNIVERSE

1. Introduction

Exist an angular, harmonic structure evident wherever we look. From the geometry of natural forms to the constants of physics, evidence points not to chaos but to coherence, governed by ratios and resonances Entropy in both physics and information theory is traditionally defined through the natural logarithm base e:  

          S = k · ln(Ω)               (1) 

Here, Ω denotes the number of accessible microstates. The logarithmic form introduces a statistical and quantum-probabilistic dimension: Boltzmann’s constant k links the microscopic uncertainty in state occupation—inherent to quantum systems—with macroscopic observables such as temperature and pressure. This formulation, centered on the transcendental number e ≈ 2,718, underpins our current understanding of disorder, complexity, and thermodynamic irreversibility.

However, we hypothesize that systems exhibiting latent self-similarity, coherence across scales, or long-range correlations may require an extended framework—one that incorporates harmonic structures encoded by φ, the golden ratio. In such systems, resonance and proportion—not just statistical multiplicity—may govern the distribution of energy, structure, and information.

1. Dual harmonic paths in angular ntropy

   Path A: the Δ₁ = 0,1 between e and φ²

Given:
φ² = 2,618, e = 2,718 ⇒

 Δ₁ = e − φ² = 0,100
                        360° × 0,1 = 36°

  Path B: the shift φ – 1,5

Taking 1,5 (using the  Pythagorean fifth 3/2) :
Δ₂= φ – 1,5 = 0,118

            ⇒ 360° × 0,118= 42,48°

  Angular convergence: the 6,48° bridge

The two angular paths differ by:
Δ₃φe = 42,48° − 36° = 6,48°
Δ₄  ⇒ ( φ – 0,118)- (e − φ² = 0,100)

      ⇒ Δ₄ residue 0,118-0,100= 0,018
                   360° × 0,018 = 6,48°

           360 x (0,018)Δ₄ = Δ₃

we will later see Δ₄ the in musical harmony where the interval 6m minor sixth  8/5 = 1,6  is φ-0,0 18 Δ₄

This shows that Δ₃ the 6,48° angular delta is the projection of a minimal structural difference of 0018 Δ₄. In this context, 0,018 Δ₄ is the harmonic residue that bridges the logarithmic (e) and resonant structures (φ).  

1. Angular frequency and decimal factor.

In physics and mathematics, especially in optics (Gabor/Fourier), the angle θ represents spatial orientation. Its inverse 1/θ yields angular frequency._(2). This mirrors how frequency is defined as the inverse of period in time: 

       f = 1/T ⇔ fθ = 1/θ               (2)

Tabla 1 Angular divisions of 360/φⁿ interpreted as frequencies. From n 3 (“0,118”) to n13 (0,691) 10 fibonacci  tones escalates for 0,1) the secuencie rich to 1/ϕ (0,6) and produces its ϕ ( - 0,118) tone (1,5) later. This decimal space works as an hologram that reflect each angle.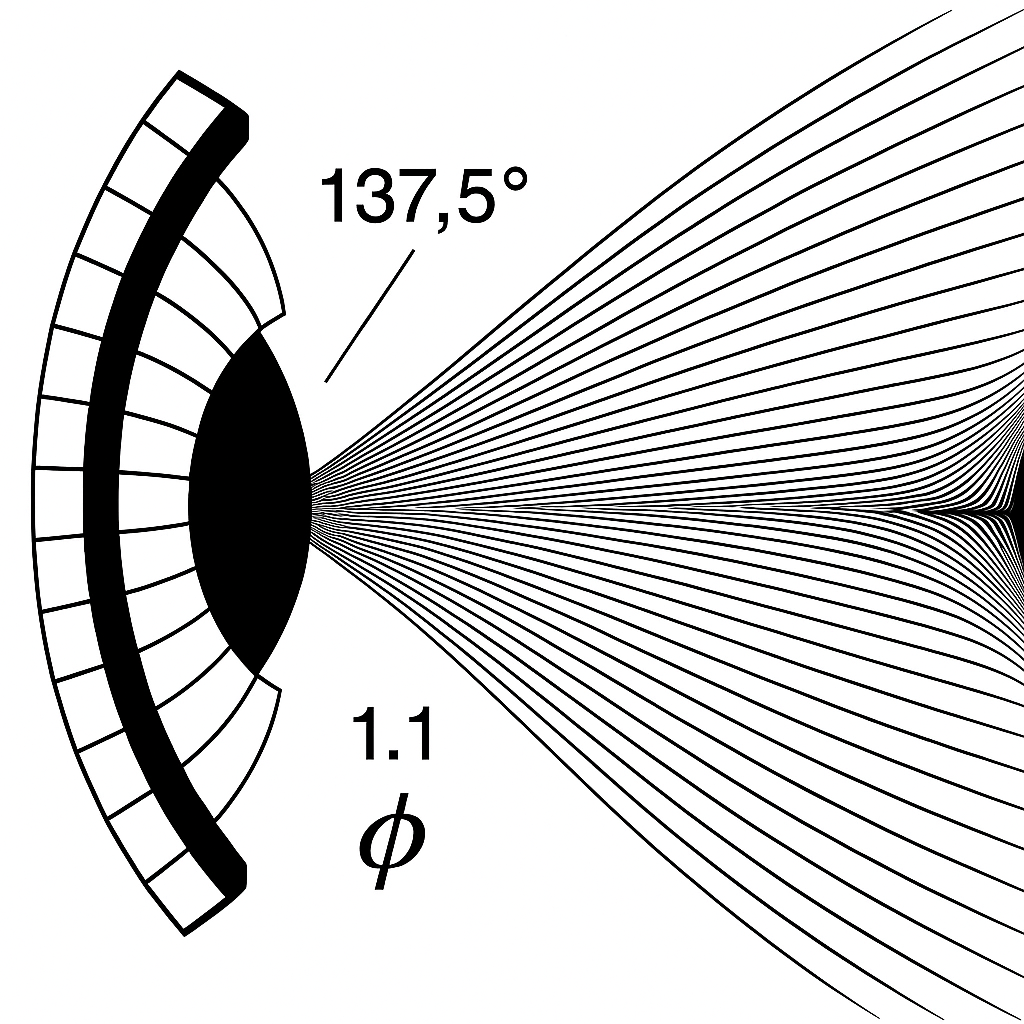 

“Resonant levels 360/φⁿ: from the golden angle (137.5°) to the reflective  threshold (0.6°) 1/φ”

Table 2 Frequency defined as 1/θ (table 1)  and its expression as musical interval, by dividing by/0,1.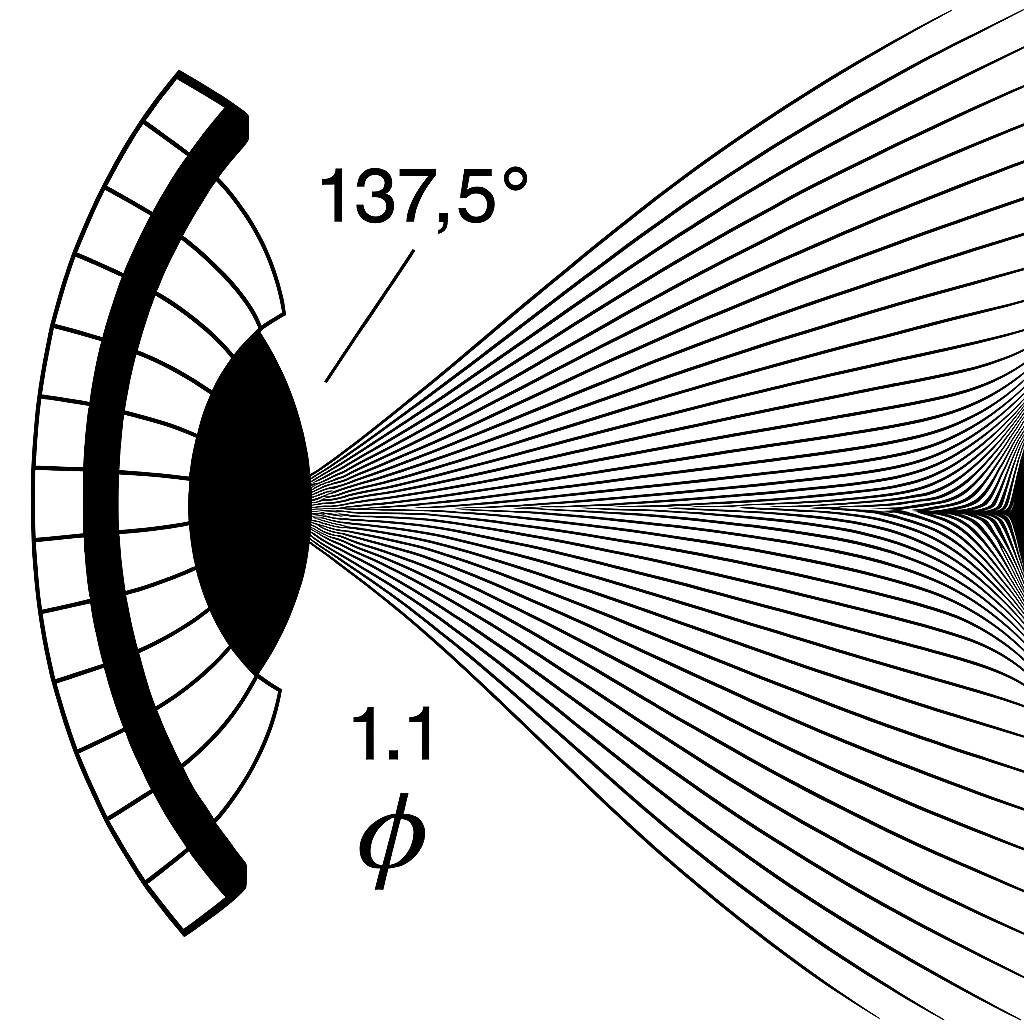

1. From spatial structures to temporal dynamics by Δ₁ 0,1.

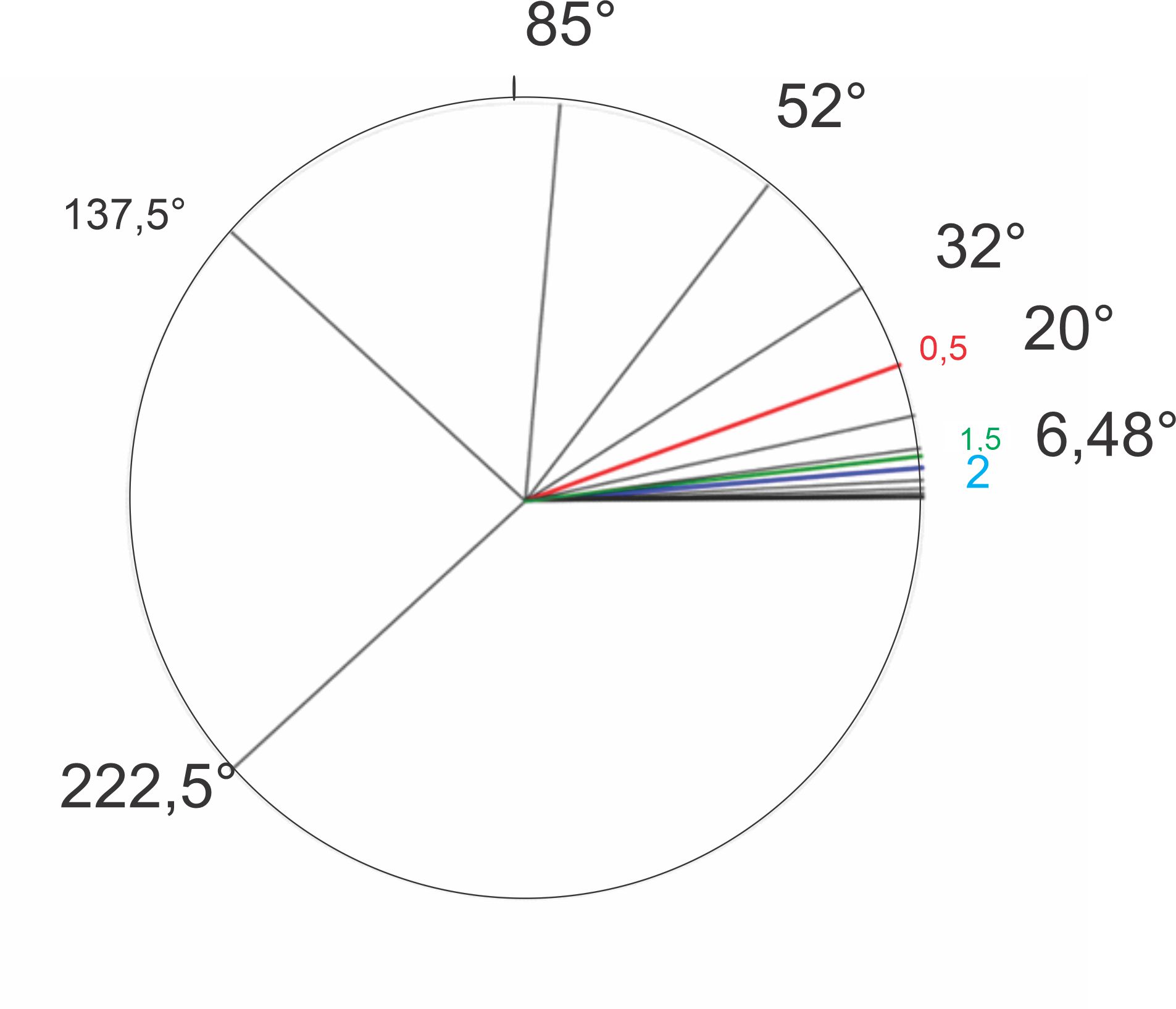  Figure 1 circular graph of angles  360°/φⁿ with 6,48° added. And key musical intervals: 0.5, 0,8, 1,3, 2, 1,5.

 1/ 6,48° = 0,1543 (angular frequency)
                0,1543 / 0,1 = 1,543 ≈ 3/2 Perfect 5 o P5

From 360ϕ²​, which yields approximately 0,0073, to 360/ϕ¹³≈0,691 which 1/ϕ​ is subtracted to obtain a structural difference of approximately 0,073 ≈ α×10 we observe a tenfold scaling of the initial value. This same factor of 10 (0,1) is used to normalize the ten frequencies that fall within this interval—spanning from 360/ ϕ² to 360/ϕ¹³, excluding both boundaries.

This constitutes the rationale behind applying a decimal normalization factor (coinciding with Δ₁=0,1) in this context: it reflects the structural window between ϕ² and ϕ¹³, and encodes it in harmonic-angular terms.

1. Relationship between the 137,5° and fourths whit its fifths.

The 137,5° angle generates, through rotation, the spiral of a sunflower_{. (3), (4)..}This angle reflect optimal paking and distribution.

In an analogous way, the 150° angle (5 × 30°) generates the musical harmony, fourth P4 do that through rotational symmetry.

Its complement in the full 360° circle is 210°,(fifth  G) which corresponds to 7 semitones of 30° each, thereby completing the 12 × 30° = 360° tonal cycle. This duality between 150° and 210° mirrors the relationship between 137,5° and 222,5°, with the sum of both pairs closing the harmonic loop and generating the entire musical structure. The difference between 137,5° and 150° is 12.5° that is ≈ 360/φ⁷ ≈ (2 x 6,48°) = 2Δ₃φe.  

 The relation 2 /1,5 = 1.33.  And the frequency ratios 3:2 (1,5) and 4:3 (1.33) are mathematically complementary, since their product equals an octave (2:1):

                    3/2 x 4/3=2 ≈ (360 x 2)

 In this sense, the perfect fifth (P5) and the perfect fourth (P4) form a reciprocal pair that spans the full octave (P8). When the ear hears a fourth, it implicitly “completes” the missing fifth needed to close the octave, and vice versa. With these three pillars—the fifth, the fourth, and the tonic—the entire harmonic system can be constructed. This duality is not only theoretical—it governs the tuning of string instruments like the cello (in fifths) and guitar (mostly in fourths) ₍₅₎  Functionally, a rising fifth corresponds to a descending fourth, and vice versa.

This angular triangle is so prevalent that nearly all songs are accompanied using this 4–5–tonic triad, often written as:  IV V  I  ₍₆₎

But in addition, each tone has a chord

formed by its tonic (I), its third (III), and its fifth (V), all of which are derived from the angular series 360/ϕⁿ. Table 1 and 2 and fig.1 also shows the successive ratio f_n /f_n−1f_n  approaches the golden ratio ϕ.  And

Fn/​fn+1​​=1/ϕ​

  Notably, at n=7, the angle is θ₇≈12,4° yielding a frequency ratio f≈0.8, which corresponds in table 2 to the major third interval 5/4.

The reciprocal of this interval, 1/0.8=1.25, and 5/4 (also=1,25) forms a complementary inversion with the minor sixth interval 8/5=1,6, establishing a phi-based harmonic inversion whit 5/8= 0,6. The 5/8 can be interpreted as a descending minor sixth—the inversion of an ascending minor sixth interval (8/5). Like ϕ and 1/ ϕ.

Table  3 . 6M 5/3 and 6m 8/5 are ratios of consecutive numbers from the Fibonacci sequence. *0,018 in 6m is also “entropic” Δ₄

When the ear hears a third 5/4 it implicitly “completes” the missing sixth needed to close the octave.

Ascending by a third and descending by a sixth both lead to the same harmonic center.

 5/4​⋅/8/5​=40/20​=2    and

6/5​⋅5/3 ​=30/15​=2

 A binary series based on 2×2n² which underlies the generation of octaves—such as C =32,  64 Hz, 128 Hz, 256 Hz—structured by powers of two and representing the backbone of traditional pitchs scaling If also we construct a 2ⁿ-based scale using φ² as the step ratio, the resulting octave sequence passes

through the frequencies 41,8 Hz and 83,77 Hz. Both correspond to F within this scale.

 Just as the 137.5° angle gives rise to spiral patterns in sunflowers and pinecones, the 150° angle generates the musical intervals associated with F, emerging uniquely from the phi-based angular progression defined by ϕ²×2ⁿ.  Also exist a ternary-binary series 3×2n which gives rise to fifths—for example, 3,  6 12… G = 96 Hz, 192 Hz, 384 Hz—forming a recursive sequence that complements the octaves structure through perfect fifth intervals. When this 96 Hz is multiplied by (1 – 0,118), it yields 84,67 Hz—this is another way (by ϕ) to calculate the F which together with 96 Hz forms the fourth and fifth relative to the base C at 64 Hz. In this framework, the fourth (F) behaves like the golden angle itself (137.5°): when rotated or expanded, it reveals its complement at 222.5°, from which the fifths (G) emerge. These harmonics, together with the octave structure rooted in C, form a coherent harmonic system where phi geometry governs musical generation. 32, 64, 96 and A 432 form this scale in which F = 85 Hz is the (150°) as a projection of 137°.

 360 x 0,018=6,48 and × 2 equals 12.5 (which corresponds to 360° / ϕ⁷). 12,5x2 gives 25° and 25°=85°- 60°. 85° is the difference between 222,5°-137,5°=360 / ϕ³. So, this 85° has your mirror in 60°, the interval 210°- 150°. In this light, the unit 85°/2 defines a phi-based semitone (42,5°), while 60°/2 defines the standard semitone of 30° (near to 32,4° =360/phi⁵). This suggests that angular units derived from φⁿ (such as 12.5°, 25°, 32,4° 42,5°, 85°) naturally generate non-equidistant but musically meaningful intervals, forming a phi-resonant scale parallel to traditional equal temperament. _{10, 11}

 Structural harmonics as bases for string teory

 If particles are strings₁₂ then strings are music—governed not by randomness, but by structured resonance. The phi-based angular model proposed here provides a concrete geometrical framework capable of classifying these vibrational patterns.

If the universe is made of vibrating structures, only those conforming to geometric and harmonic coherence can persist. The string theory₉ should account for the harmonic intervals presented here. The frequency ratios explored in Tables 1, 2, and 3 are physically mandated constraints for any viable theory of vibratory matter.

 7 . Emergence of α ≈ 1/137: The law of angular normalization.

 On the table 1 appears  

   360°/φ2 =137,5            (3)

and  ⇒ 1/θ ≈ 1/137 =0.00729.

 which remarkably approximates the fine-structure constant

IIt suggests that α is not merely a fitting parameter in quantum electrodynamics, but the harmonic residue required to close the angular cycle of a φ-based fractal.

 This observation leads to the relation:

                    ϕ²/ α ≈360°

is signals that α may emerge from a resonant geometry that also governs the vibrational structures of strings₍₁₀₎, whether in instruments or fundamental particles.

This leads to the Law of angular normalization, which posits that each fractal progression (ϕⁿ) naturally generates frequencies or nodes that close coherently into the angular cycle. α is simply the first such structural residue, revealing a harmonic scaffolding underlying physical constants.

Although equation (4) is just one possible relation, additional resonant values emerge from powers of φ. For instance:

ϕ²⁴ yields a value whose reciprocal

1/θ≈288 Hz which equals 2× (12×12)=288. The only Fibonacci number that is a perfect square is 12² (144). This value appears within a structured frequency scale that includes:

C = 64 Hz, F = 84 Hz, G = 96 Hz, D = 144 Hz, D = 288 Hz, A = 432 Hz

Other φ-based projections include:

• ϕ¹⁷ yields 0,100° and 1/θ=10 Hz and multiplied by 8, this gives 80 Hz, which corresponds to an E in this same scale.
• ϕ¹⁸  yields 1/θ≈16, which equals 64/4, two octaves down C = 64 Hz.
• ϕ²⁰ gives  ≈42,37 , which matches the F within the same phi-aligned scale that includes E 10 C = 16 Hz and F = 42 Hz.
• ϕ³ 1/θ = 0,0118 x 0,1 =0,118 = x 10 de ϕ³ a ϕ¹³

α encodes the normalization needed to close physical cycles in 360° (electrodynamic level).

 0,118 encodes the correction needed (ϕ -1,5) to open self-similar spirals (perceptual and geometric level).

 The angle 360/ϕ¹⁷ ≈ 0.1008°. This angular value (also corresponds E) is the structural delta Δ₄ = e − ϕ² ≈ 0.100°, suggesting that ϕ¹⁷, like 0.018 (which links the minor sixth 6m with φ and with e), acts as a harmonic connector between exponential growth and fractal structure.

 Harmonic Entropy Law?

 We propose the following formulation of entropy:

      S=k⋅ln(e/φ​)              (5)    

 e/ϕ ≈2,718/1,618=1,679      

numerically, this formulation yields:

                       S≈k⋅log 1,679 ≈k⋅0.518

 Interestingly, this same value can be expressed through a structural correction to the golden ratio:

  S=  K.log (ϕ+1/2⋅(0.118+004)      (6)

 Equations (5) and (6) 210° from the 222,5° (360/ ϕ) en la tabla 1 (And its corresponding frequency is 0.08).

Moreover, in the frequency domain, 0,118 reappears in the spiral of resonancies of phi

     360/ϕ^11.236 ​=ϕ≈1,618, Notably, the exponent 11.236 contains a structural residue:

      11.236=11+0.236 with    

            0.236=2×0.118

And this is the limit of angular contraction, because 360/ϕ¹³=0.678.

  ≈1/ϕ and whith 1/θ reemerge

                (1)/1/ϕ =ϕ 

as a frequency  = 1,47. This implies that the spiral based on 360/ϕⁿ folds back upon itself at this limit, closing a harmonic cycle         

Besides:

               ϕ−0.678=0,94 ≈(8⋅0.118)  and

360/ ϕ¹³=0,691-1/ ϕ=0,0731= α  x 10. And here is closed 10 steps of 10x.  

indicates that this difference between the 13th angular phi node and the inverse golden ratio coincides with a decimalized form of the fine-structure constant α. This suggests a structural "closure" over ten phi steps (from φ³ to φ¹³), each scaled by Δ₁ = 0.1, reinforcing the harmonic significance of this range.  In this framework, the traditional view of entropy as disordered microstates is thus replaced by a harmonic deformation principle, where energy, structure, and disorder emerge from quantized angular shifts.

 Fibonacci time crystals and the emergence of frequency

The so-called Fibonacci time crystals _[13][14] do not reveal a “new form of time,” but rather the emergence of structured frequencies as a system crosses specific angular thresholds defined by the series

θ_n=360/ϕⁿ. In this model, time is not a pre-existing background dimension, but an emergent phenomenon that arises only when angular configurations resonate and collapse into periodic or quasi-periodic frequencies—analogous to how a hologram reveals its image when coherently illuminated.

The Fibonacci sequence efficiently reproduces these non-periodic angular steps. When activated, it does not generate time per se, but rather a structured frequency field with rhythm and proportional scaling. In this view, frequency precedes time, and geometry precedes frequency.

Consequently, entropy—traditionally defined through the arrow of time—must also be redefined. If time is not fundamental but emergent from angular resonance, then entropy becomes a derived effect, expressing the unfolding of coherence or decoherence within a harmonic structure. It is not disorder measured over time, but structural displacement from resonance within a geometric configuration.

Thus, time, entropy, and rhythmic perception are not fundamental properties, but emergent effects of non-linear angular geometry governed by phi-symmetries.

The golden ratio φ and the correction 0,118 respect a 3/2 act as organizing principles behind the distribution of states. In this framework, Δ₁ 0.1 and Δ₂ 0,118Δ₃φe and Δ₄ (0,018) are not arbitrary decimals, but units of entropic deformation over a geometrical base: they mold how information expands from structure.

This is most clearly demonstrated in the angular interval between the two fundamental nodes of the spiral: 360° / φ=222,5  and  360° / φ² =137,5

The difference between them is:

         Δθ=222,5°−137,5°=85°,

 which decomposes exactly into:                                   

            Δθ = 720⋅0.118.

Thus, the space between ϕ and ϕ² is quantized into (360 x 2) discrete angular steps, each of size 0.118°, the revealing that spiral’s harmonic architecture is fundamentally granular. The midpoint of this quantized sequence occurs at:

  θ=222,5°−(360° x 0.118)=180°,

 marking a perfect diametral opposition between 360/φ and 360/φ². This confirms that the value 0.118° discretizes the 85° arc into two symmetric halves, each composed of 360 units, placing 180° as a central axis of angular resonance.

10. Conclusion

The 360°x 0,118 Δ₄ =6,48° = (360 ϕ⁷/2) may serve as a bridge between entropy and harmony. The fifth and its residue with φ (1,5+0.118) act as translators. The numerical identity represents as 360/ph²= α^—1

​​​     0.0072705≈ 0.00729927

is a revolutionary insight into the possible harmonic origin of one of physics’ most fundamental constants. We refrain from asserting whether this structural formulation constitutes a new entropy definition. Instead, we highlight its recurring emergence across multiple angular and frequency domains. Whether this reflects a hidden order or merely a numerical coincidence is left open to future exploration.

1. References

• Shannon, C. E. (1948). A Mathematical Theory of Communication. Bell System Technical Journal, 27(3), 379–423.
• Gabor, D. (1946). Theory of Communication. Journal of the Institution of Electrical Engineers, 93(26), 429–457.
• Vogel, H. “A better way to construct the sunflower head.” Mathematical Biosciences3–4 (1979): 179–189.
• Jean, R.V. Phyllotaxis: A Systemic Study in Plant Morphogenesis. Cambridge University Press, 1994.Penrose, R. (2004). The Road to Reality: A Complete Guide to the Laws of the Universe. Jonathan Cape.
• von Helmholtz, H. (1954). On the Sensations of Tone (A. J. Ellis, Trans.). Dover Publications. (Original work published 1863)
• Mazzola, G. (2002). The Topos of Music: Geometric Logic of Concepts, Theory, and Performance. Birkhäuser.
• Green, M. B., Schwarz, J. H., & Witten, E. (1987). Superstring Theory (Vols. 1–2). Cambridge University Press.Livio, M. (2002). The Golden Ratio. Broadway Books.
• Penrose, R. (2004). The Road to Reality: A Complete Guide to the Laws of the Universe. Jonathan Cape.
• Feynman, R. P. (1985). QED: The Strange Theory of Light and Matter. Princeton University Press.Nottale, L. (2011). Scale Relativity and Fractal Space-Time. Imperial College Press.
• Ramírez Z Enrique A. Placer o dolor “funcionalidad y manejo del cuerpo energético” Publicaciones Edwin Medellin Colombia. 1988
• Ramírez Z Enrique A. “Todos somos uno” Publicaciones Edwin Medellin Colombia. 1997
• Kaku, M. (1999). Introduction to Superstrings and M-Theory. Springer.
• Wilczek, F. (2012). Quantum Time Crystals. Physical Review Letters, 109(16), 160401.Svozil, K. (1996). Randomness and Undecidability in Physics. World Scientific.
• Else, D. V., Bauer, B., & Nayak, C. (2016). Floquet Time Crystals. Physical Review Letters, 117(9), 090402.
  
  

+