
Every molecule is an adventure
Some things just take time. Sending a probe to a distant planet, or clinical trials for a vaccine, have intrinsic limitations on how quickly they can be accomplished, even if everything goes to plan. The synthesis of a molecule that has not been made before can also take considerable time. Not because any of the chemical reactions involved are necessarily slow, but rather because every molecule is an adventure. Former US Defense Secretary Donald Rumsfeld famously discussed the problems of 'known knowns', 'known unknowns' and 'unknown unknowns' in strategic planning. When it comes to chemical synthesis it's often the unknown unknowns - aspects of the desired transformations that the chemist doesn't realise they don't understand - that form the bottlenecks in particularly novel synthetic strategies.
In 2011, Jon Beves, then a post-doc in my group (now an Associate Professor at the University of New South Wales), came up with the exciting idea of synthesising a molecular endless (74) knot from a woven 3x3 grid. The 74 knot is an iconic topology, a basic motif of Celtic interlace, the smallest Chinese knot, and one of the eight auspicious symbols (the Ashtamangala) common to many Eastern religions and philosophies, where it represents the union of wisdom and method. It is also the basic repeat unit of a plain weave, the most basic weaving pattern for fabrics. Clearly its synthesis would open up new research directions and possibilities in materials science. Jon's original sketch for the concept (on pages torn from a 2011 RyanAir magazine!), together with the first design we worked on (developed by Jon and then-PhD students Jean-François Ayme, Chris Campbell and Jon Danon during our annual group conference, at that time held on the shores of Loch Tay in Scotland), are shown below in Figure 1.

However, there was an obvious problem with the proposed synthetic strategy: a quick search of the chemistry literature confirmed that woven 3x3 molecular grids were unknown. And there could be good reasons for this: although in our everyday world sticks can be woven so that they hold together only because of the pressure exerted between the sticks at the crossing points, for a woven supramolecular structure such stresses would impose limitations and tolerances on metal-donor distances and geometries of the coordination sites. Our early designs for 3x3 interwoven grids featured strong terpyridine-like coordination motifs for the difficult centre-of-the-cross position, with weaker binding sites at ends of the strands based on thiazolo[5,4-d]thiazole (TTZ; a potential heterocyclic ligand introduced by Peter Steel's group a few years earlier). Although these early designs did not themselves form 3x3 interwoven grids, they provided the basis for later successful designs.
Gridlock
One of the ligand strands we investigated is shown in Fig. 2. Each strand contains a TTZ-pyridine coordinating motif at each end, with an additional central TTZ-pyridine core intended to provide the key internal site. Treatment of the ligand with Zn(OTf)2 in apolar solvents showed a complex product mixture with some evidence (by mass spectrometry and 1H NMR) for coordination of two strands through a corner join (Fig. 2).
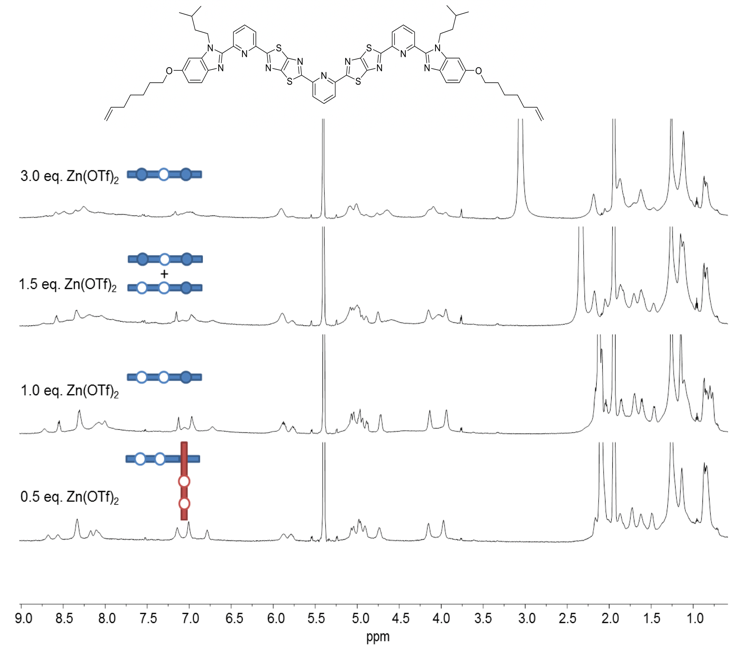
Fig. 2. 1H NMR (600 MHz, 298 K) spectra of titration of a ligand strand design with Zn(OTf)2 in CD3CN/CD2Cl2.
As the binding between zinc(II) and the central site of the ligand appeared to be insufficient in this design, electron-donating methoxy groups were added to the pyridine groups (Fig. 3). The new ligand also formed corner complexes with Zn(OTf)2. There was also mass spectrometric evidence for assembly of four strands into a square, but still no sign of the elusive six-strand interwoven grid.
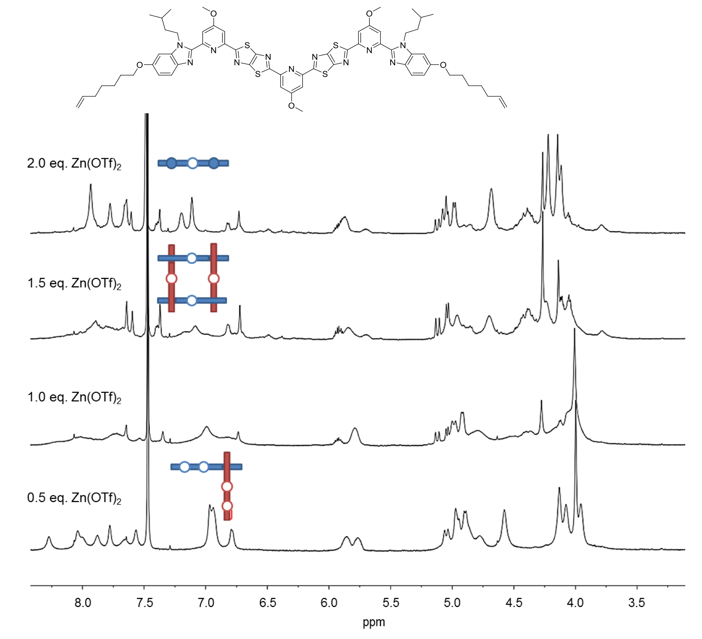
Fig. 3. 1H NMR (600 MHz, 298 K) spectra of titration of second ligand strand design with Zn(OTf)2 in CD3CN/CD2Cl2.
The coordinating ability of the central pyridine unit was further enhanced by replacing the methoxy group with a dimethylamino one (Fig. 4), with the outer pyridines reverting to being unsubstituted at the 4-position to maximise the difference in coordination efficacy between the outer and difficult internal sites. When 1.5 equiv. of Zn(OTf)2 was added to this ligand, the theoretical stoichiometry required for nine zinc cations to bind to six ligands, a complicated mixture of species was again observed but still with no sign of interwoven grid formation (Fig. 4).
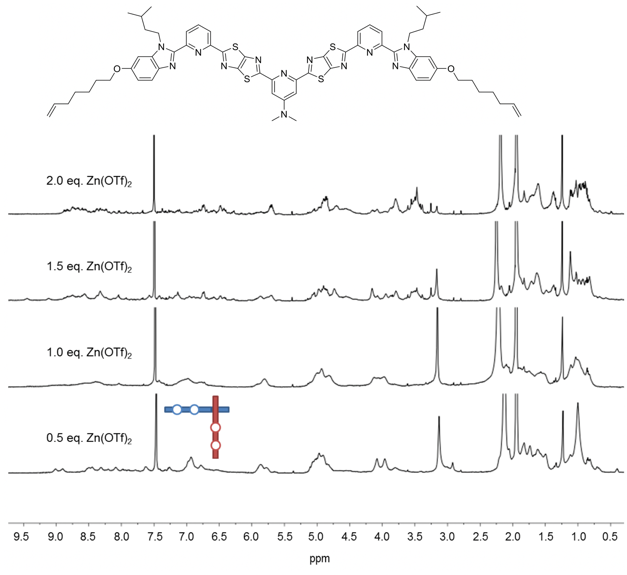
Fig. 4. 1H NMR (600 MHz, 298 K) spectra of titration of third ligand strand design with Zn(OTf)2 in CD3CN/CD2Cl2.
At this point, postdoc Jean-François Lemonnier recalled that the X-ray crystal structure of the Solomon link constructed from the smaller 2x2 grid was of the BF4- salt, and featured a well-ordered BF4- anion in the central ‘square’ of the 2x2 interwoven grid. He switched from using Zn(OTf)2 to coordinate the ligand strands to Zn(BF4)2 with immediate—extraordinary—results. Within 5 minutes of mixing the ligands with Zn(BF4)2in the required 3:2 stoichiometry (i.e. 9 metals to 6 ligands), the interwoven 3x3 grid assembled quantitatively (Fig. 5)!
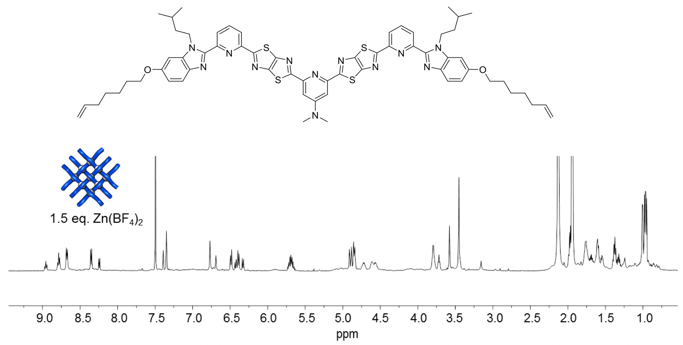
Fig. 5. 1H NMR (600 MHz, 298 K) spectra of titration of third ligand strand design with Zn(BF4)2 in CD3CN/CD2Cl2.
The X-ray crystal structure of the interwoven 3x3 grid confirmed its architecture and ring-closing olefin metathesis subsequently afforded the 258-atom-long, closed loop, 74 endless knot (along with a simple macrocycle and a Solomon link). Figure 6 shows the structure of the 74 knot coordination complex (with 6 x Fe(BF4)2) based on the X-ray structure of the 3x3 interwoven grid with modelled cyclized end groups. The X-ray structure also showed the key role played by the BF4- anions: four of them bind in the square cavities formed between the criss-crossed coordinated ligand strands (Fig. 6). The binding energy provided by those interactions are sufficient to stabilize the entire structure to the extent that the formation of the woven grid becomes favourable.
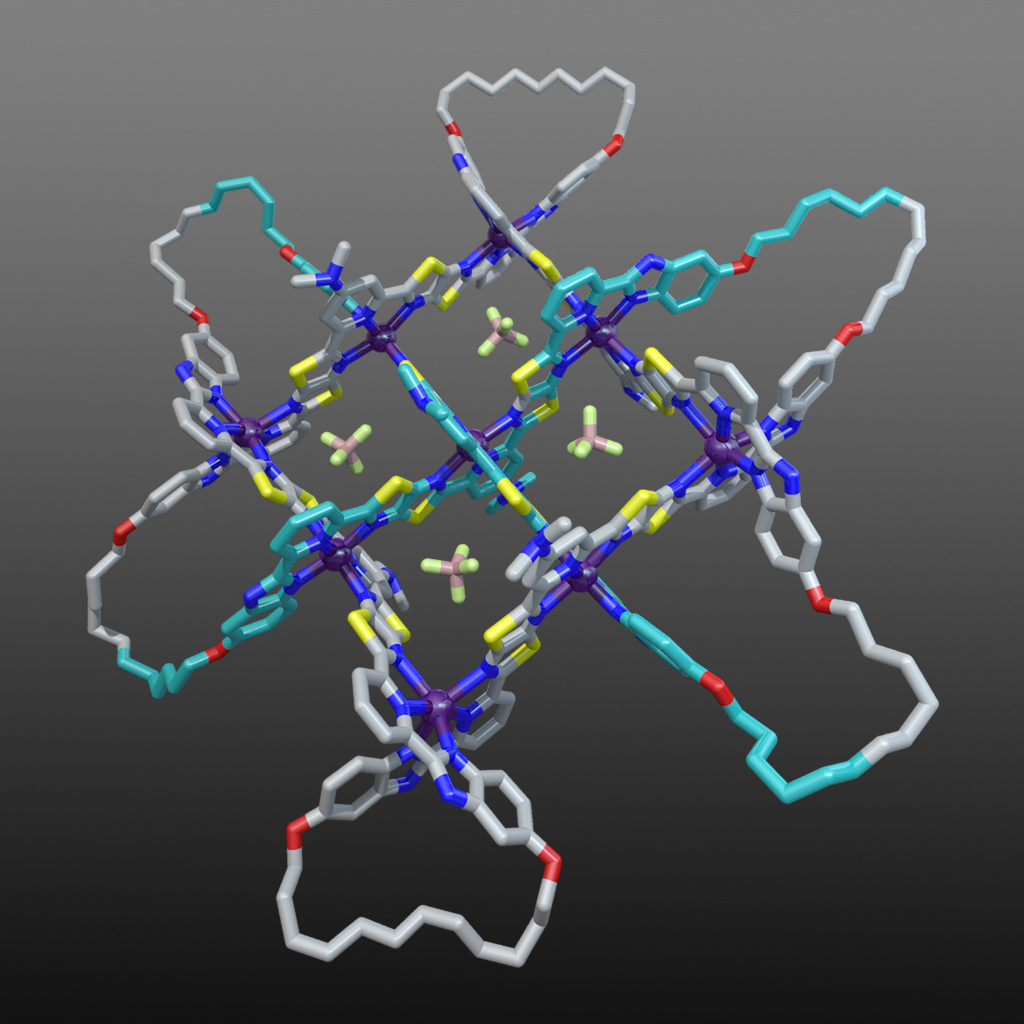
An endless challenge
Despite a decade of design and redesign it was ultimately an unanticipated BF4- template effect, tried only because of the recognition of interactions present in an X-ray crystal structure of a related Solomon link, that led to the assembly of the key intermediate, an interwoven 3x3 grid. The story of the synthesis of the molecular endless knot illustrates well how cutting-edge scientific research often actually proceeds: scientists continually face challenges for which they do not know quite enough to definitely be able to solve. But once a problem is solved (by some combination of skill, observation, reasoning, screening and, occasionally, luck!) the answer provides insights that makes future challenges easier. In this way science advances, one puzzling bottleneck at a time. The practical significance of the preparation of the endless (74) knot in molecular form is to be found in the lessons learnt from its synthesis, which opens the way for the bottom-up assembly of woven polymer chains and other knotted and entangled molecules and materials.

Fig. 7. The endless knot is a familiar feature in traditional Chinese art. This original artwork was created for the author by Shanghai artist Ying Wu. Image credit: Ying Wu and Jo Richers; jorichers.com.
[An alternative version of this post, 'Endless forms most beautiful', is available on the Leigh group website, www.catenane.net]
Follow the Topic
-
Nature Chemistry

A monthly journal dedicated to publishing high-quality papers that describe the most significant and cutting-edge research in all areas of chemistry, reflecting the traditional core subjects of analytical, inorganic, organic and physical chemistry.


Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in