Machine learning the Hohenberg-Kohn map for molecular excited states
Published in Chemistry

Density functional theory (DFT) provides a powerful framework in which the energy and density of a quantum many-body system can be computed with knowledge of only the atomic coordinates, number of electrons, and spin state. DFT’s relatively low computational cost (compared to wavefunction methods) and reasonably high accuracy has seen its widespread adoption to describing the electronic ground state of molecules and materials. However, the foundational Hohenberg-Kohn theorem (HK) of DFT tells us that the electron density uniquely determines not only the ground-state energy, but all properties of a molecular system, including electronically excited-state energies. This is important because electronic excitations underlie numerous processes of interest, including photochemistry, solar energy conversion, photosynthesis, DNA damage, and photomedicine. There is thus significant interest in developing low-computational-cost DFT methods for excited states; however, an exact functional which maps from ground-state density to excited-state energy is unknown. This motivated us to consider data-driven machine learning (ML) approaches to constructing a functional for excited states.
In previous work, two of us were involved in developing a ground-state ML functional, starting from a condition established by the HK theorem that the external potential (the nuclear Coulomb potential experienced by the electrons) uniquely determines the density, suggesting that the external potential is an excellent choice for an ML descriptor. The resulting ML-HK functional achieved quantitative accuracy compared to the approximate theoretically constructed functional on which it was trained. Follow-up work showed that the ML-HK functional could be corrected by training against “gold-standard” coupled-cluster calculations to yield energy predictions with chemical accuracy (< 1 kcal/mol relative errors).
The previous successes inspired us to extend the ground-state ML-HK method to represent excited states. One twist that we anticipated needing to address is the propensity for electronic excited states to cross (ie swap their order) with each other as nuclear positions are varied. The regions where these crossings occur, known as conical intersections, play a critical role in governing the outcome of light-initiated processes. Consequently, we required our excited-state functional to perform well in these regions. A challenge however is that the energy and density of an electronic state vary rapidly in the vicinity of crossings. This means that a ML functional trained on only a single state at a time would need a large amount of data from many molecular conformations near to the electronic crossings in order to achieve chemical accuracy. Such a functional would be computationally expensive both to train and to evaluate in order to generate energy predictions on untrained samples. Our idea to overcome this challenge was to learn a single functional that maps multiple states’ densities (ground- and excited-state) to their respective energies rather than to learn a functional of a single density. In so doing, the functional, which we call a machine-learned multistate Hohenbeg-Kohn map (ML-MSHK), contains information about all electronic states involved in a crossing by construction.
To test our idea, we trained the ML-MSHK functional for the lowest two electronically excited states of the organic molecule malonaldehye (MA - see figure below for a molecular graphic). This molecule is of particular interest since its ring conformer can undergo an intramolecular proton transfer reaction. The kinetic barrier to proton transfer is significantly reduced when the molecule is excited from the ground state to the second excited state (S2), thus MA is representative of an important class of molecules that undergo excited-state proton transfer reactions. However, because of the high degree of flexibility in this molecule, torsional motions on S2 bring about an electronic crossing with the first excited state, S1, which has a higher barrier to proton transfer than the ground state. Electronic transitions from S2 to S1 therefore preclude proton transfer. Because of these features, MA serves as an ideal molecular test for our ML-MSHK functional, both in its ability to describe how a reaction responds to electronic excitation and its handling of electronic crossings.
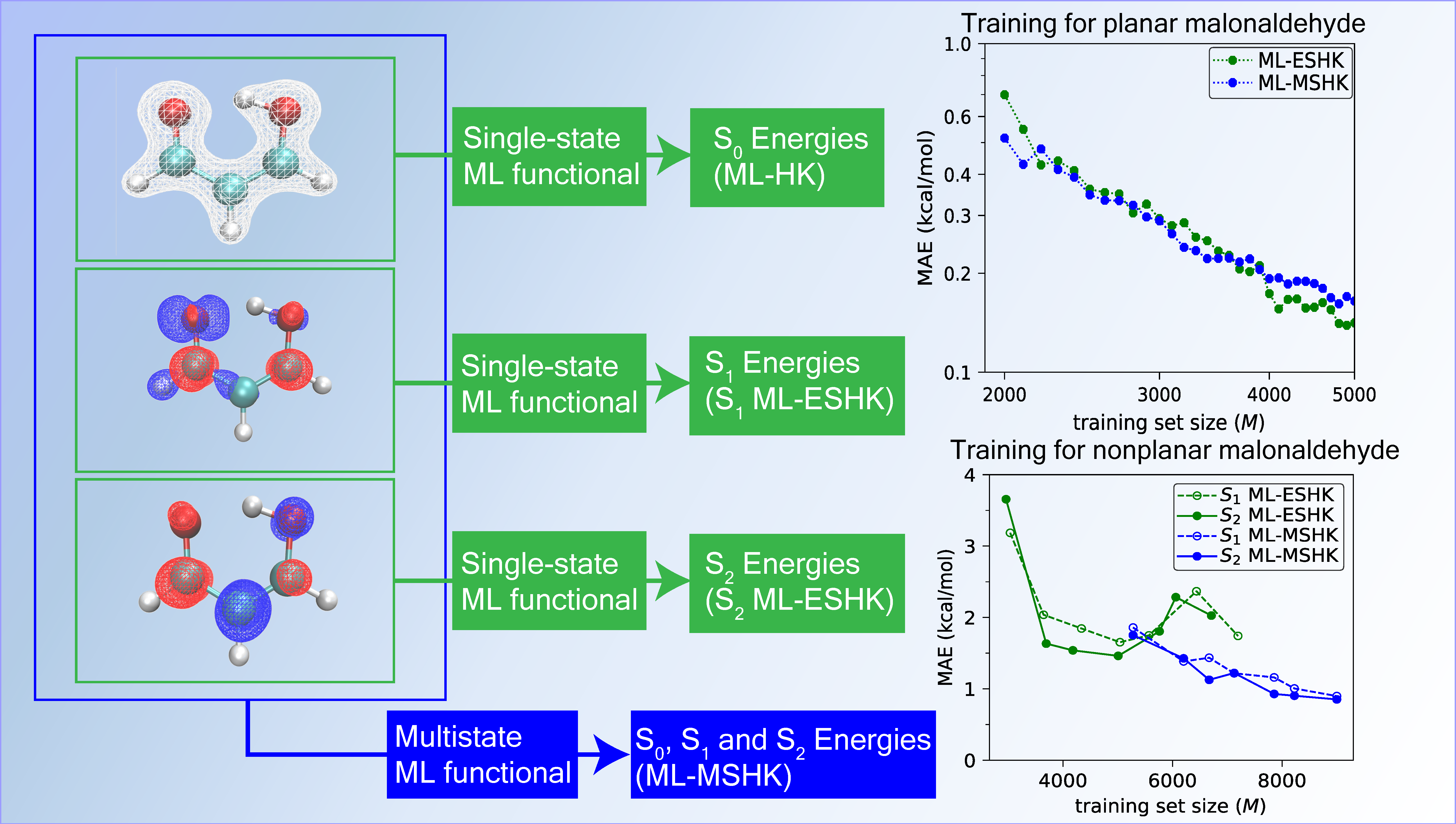
Since we sought to obtain a functional that worked equally well for excited states and for the ground state, we started by considering excited-state structures of MA sampled with a restraint of planarity, to prevent S2/S1 crossings, and to facilitate direct comparison to the previous ground-state work on this molecule. As we see in the figure above, the prediction error of the trained functional on these planar excited-state MA structures improves systematically with training set size, ultimately attaining an accuracy below 0.2 kcal/mol, comparable to the previous ground-state functional, and well within chemical accuracy. Furthermore, we obtained comparable accuracy of the functional regardless of whether it was trained using only a single excited-state’s information (ML-ESHK, green curve) or as a multistate functional (ML-MSHK, blue curve). This implies that more general functionals can be learned with no loss in accuracy on the excited state of interest. The low computational cost of the resulting ML-MSHK functional then allowed us to run thousands of excited-state trajectories, which revealed that by suppressing the S2/S1 electronic transition with a restraint of planarity, the proton transfer reaction proceeded unhindered on an ultrafast timescale (~20 femtoseconds).
Finally, in order to explore the performance of the functionals near electronic crossings, we relaxed the restraint of planarity for MA. The resulting energy prediction errors are shown in the lower panel of the figure. There, we clearly see the benefit of training a multistate functional: the single-state ML-ESHK functionals (green curves) show a saturation of the error as the training set size is increased, and never reach chemical accuracy, while the ML-MSHK functional again systematically improves in accuracy as the training size is increased. Learning a functional for multiple excited states simultaneously seems to be the key to accurate prediction of properties of states near their crossings. We view this as a major step towards a universal machine-learned functional for both ground and electronic excited states of molecules.
If you are interested in our work, you are welcome to have a look at our paper published in https://doi.org/10.1038/s41467-022-34436-w.
Follow the Topic
-
Nature Communications

An open access, multidisciplinary journal dedicated to publishing high-quality research in all areas of the biological, health, physical, chemical and Earth sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Women's Health
Publishing Model: Hybrid
Deadline: Ongoing
Advances in neurodegenerative diseases
Publishing Model: Hybrid
Deadline: Mar 24, 2026



Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in