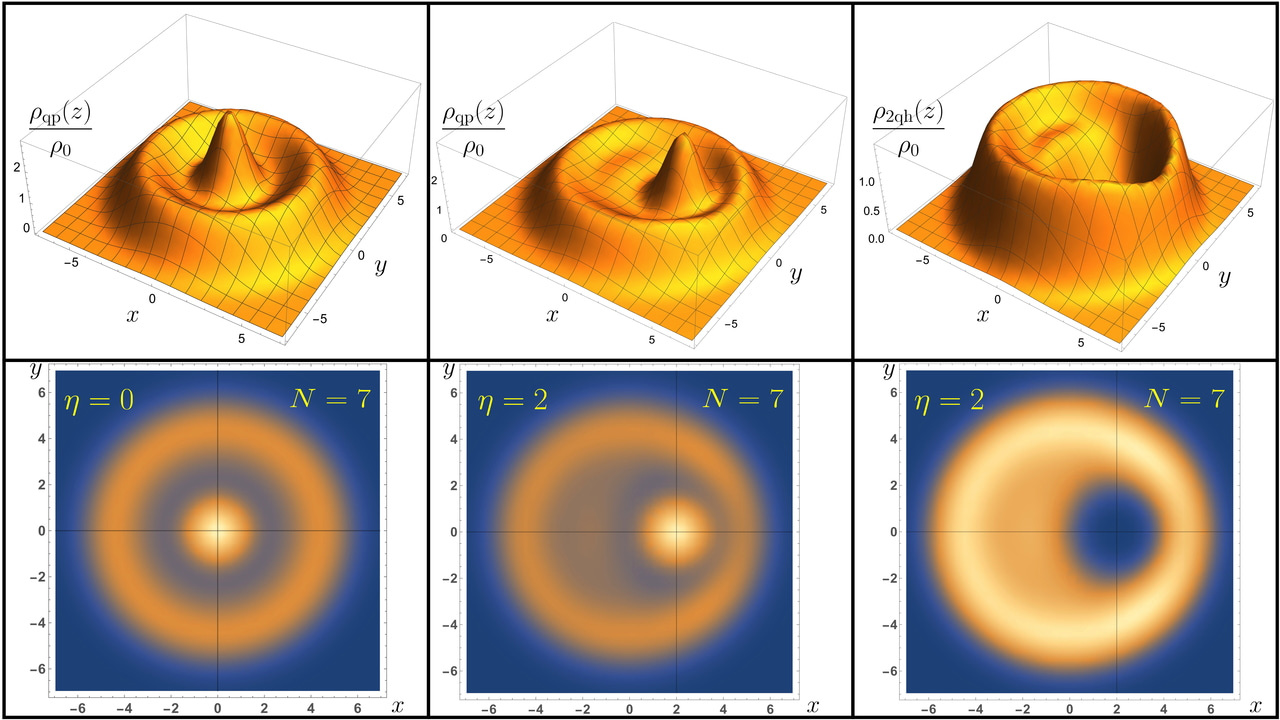
Fractional quantum Hall fluids epitomize the best-known examples of strongly interacting topological quantum matter, hosting a set of remarkable phenomena such as fractional charge and exchange statistics. These properties are fascinating not only from a fundamental physics standpoint, but also for their potential to robustly encode quantum bits for information processing. The way these systems process quantum information is by exploiting the braiding properties of the fluid’s elementary excitations known as anyons. These topological excitations can be manipulated by external means in ways such that their world lines form braids effecting specific quantum gates. A potential advantage of this scheme over others is the intrinsic resilience against decoherence originating from their topological protection, thus leading to an intrinsic fault-tolerant way of quantum computation.  

     An important observation made by Robert Laughlin in the 1980s was that the bulk elementary charged excitations of a stable quantum Hall fluid with filling fraction 1/M, with M being an odd integer, are quasiholes and quasiparticles with fractional charge ±e/M, where e is the elementary charge of the original electron. Laughlin advanced a way of generating these elementary excitations by proposing respective wave functions. Furthermore, it was argued that by braiding those excitations one would obtain the equivalent of particles displaying fractional exchange statistics of phase 2π/M (that are neither fermions or bosons). This is the reason why Frank Wilczek’s coined these topological excitations anyons. Another insightful conjecture advanced in the 1990s by Xiao-Gang Wen addressed the way edge excitations correlate at long-distances, establishing a connection to the topological nature of the bulk fluid, a so-called bulk-boundary correspondence. By mapping the physics at the edge to that of a Luttinger liquid and proposing an effective edge theory description, Wen provided our best guide toward understanding electronic transport between edges of quantum Hall systems.

     The physical mechanism supporting Laughlin’s intuition was that of magnetic flux insertion (in the case of quasiholes) or removal (in the case of quasiparticles (quasielectrons)) over the the stable incompressible quantum Hall fluid with filling fraction 1/M. The addition of M quasiholes (quasiparticles) at the same spatial position should be equivalent to adding one hole (particle) at that same position. Although for quasiholes this mechanism does work, this is not the case for Laughlin’s, or any other, quasiparticle proposal. The work in Commun. Phys. 5, 171  (2022) resolves this conundrum. In other words, it develops the quasiparticle (quasielectron) operator fulfilling Laughlin’s intuition. Specifically, the solution reveals a profound and exact fractionalization procedure that allows for a very natural fusion mechanism of quasiparticle generation (see Figure above).  As a result, the associated quasielectron wave function differs from Laughlin’s original proposal and other suggestions since. Furthermore, this quasiparticle has the correct fractional charge and statistics. Indeed, the latter statement is rigorously proven by the topological equivalent of an adiabatic Aharonov-Bohm type process for which the Berry connections for one and two quasiparticles are analytically determined for the first time.

      In Phys. Rev. B 98, 161118(R) (2018), the needed theoretical path linking the microscopic description of these strongly interacting systems to their universal behaviors was developed. This approach underscored the fundamental role Entangled Pauli Principles play in unveiling universal structures encoded in the root state (or DNA) of fractional quantum Hall states. It was demonstrated how universal properties of these systems are encoded in their DNA. The question of how the bulk universal properties relate to the edge/boundary excitations is addressed in Commun. Phys. 5, 171 (2022), which advances a conjecture that enables a demonstration of the universal long-distance behavior of edge excitations in weak confining potentials.  Strikingly, the asymptotic long-distance edge physics derived in this manner matches Wen’s earlier hypothesis and hints at a possibly general powerful computational recipe for predicting edge physics.