Imagine there is a solid cube with elasticity. If we compress it evenly, common sense tells us that every point in the cube will move towards the center. This solid elastic behavior is called the affinity, which indicates to what extent the displacement field of internal mass points depends on the external strain. Intuitively speaking, the conventional elastic solids in our daily life are completely affine. Namely, the displacement field of the internal mass points corresponds precisely to the boundary strain. However, this common-sense does not apply to the mechanical response of the network consisting of nodes connected by central-force bonds.

On the contrary, the completely affine mechanical responses throughout the entire network are the exception rather than the rule. It is only guaranteed to occur in absolutely homogeneous systems and lattices with one node per unit cell. As illustrated in Fig.1, when we compress a network, its internal displacement field tends to be chaotic, and its mechanical responses are very complicated.

_{Fig.1 At different coordination numbers z, the figure show the displacement fields of nodes under shear or compression.The higher the z, the higher the affinity of the system.}

The network's affinity is associated with its equilibrium matrix containing all the topological and geometrical characteristics of a network, such as the nodes' spatial distribution, connectivity, bond length distribution, etc. However, due to so many factors involved, the related research, including under what conditions a network can achieve completely affine or close to completely affine, is still rarely carried out, leading to insufficient knowledge about a network's affinity.

Jamming is a unique state in material packing that occurs on various occasions, such as the jam of particles, emulsions, and foams. The jamming state can be abstractly understood as a system composed of close-packed balls, which can be further simplified to a network. The packing derived network near the marginal jamming state has very low affinity, which is believed to be the reason for its diverge moduli ratio.

We found that the affinity in the packing derived networks is only related to the degree of connectivity z. As z increases, an affine phase transition that corresponds to a fundamental topology change will occur at a particular z in two dimensions (2D) and three dimensions (3D). For example, in the two-dimensional case, when z=6, i.e., the entire network is fully triangulated and reaches the maximum value of connectivity under the condition of an invariant topological characteristic, the network tends to be completely affine. For a non-affine network, the shear and bulk moduli can be separately adjusted by removing specific connections. One can even obtain a network with a negative Poisson ratio in this way.

Moreover, the affinity is a local property. Once an area is fully triangulated, the area will be completely affine. Thus, we can add "redundant" cross-connections to these regions and not change the global response (Poisson ratio) of the system to the external strains but enhance the rigidity of the structure. These findings improve the adjustment freedom of the network's mechanical response and provide new ideas for the design of mechanical metamaterials.

_{Fig.2 Three different 3D printed networks and their mechanical responses to the consistent press strain.}

Our findings can be extended to 3D. Similar to the 2D case, we can also add some specific bonds to stiffen the network without changing its global or local affinity. In 3D, if the added "cross bond" is inside the fully tetrahedralized region of a packing derived network, the global affinity remains invariant. Three 3D printed networks shown in Fig.2 demonstrate how to manipulate the mechanical responses of the networks based on affinity. From the top to the middle panel, non-cross bonds are added, and z increases from 7.696 to 9.312, which tunes the affinity and the mechanical response and realizes the non-affine elasticity. However, from the middle to the bottom panel, "cross bonds" are added, and z increases from 9.312 to 10.432, which locks affinity and mechanical response and achieves the affine elasticity.

We apply identical external press strain to these three systems and compare their internal strain fields, determining the essential elastic responses such as affinity and Poisson's ratio. As illustrated in the right two columns, the top and middle panels exhibit a significant difference in their internal strain, demonstrating distinct elastic responses due to our non-affine tuning operation. However, the middle and the bottom panels show almost identical internal strain, verifying the same elastic responses due to our affine locking operation. The forces generated by this strain are also measured as 7.86 N, 10.47 N, and 12.24 N, respectively, confirming the expected increase of system rigidity with respect to bond addition.

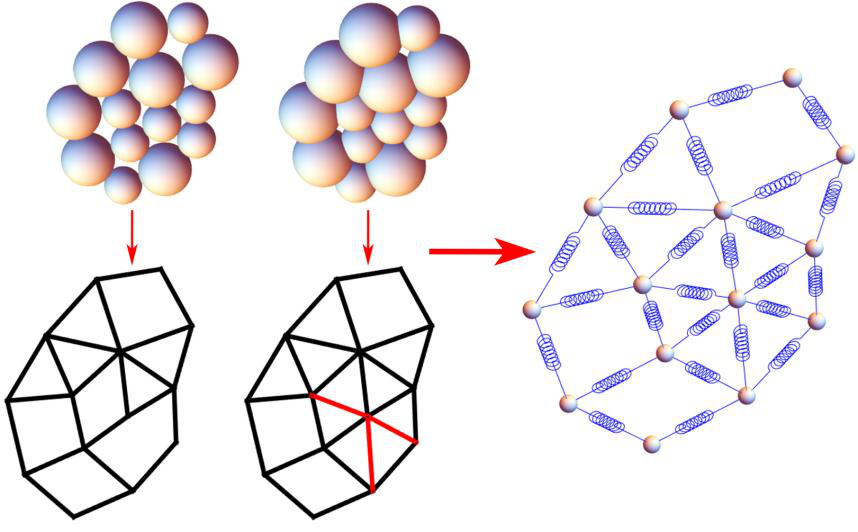
_{Fig.3 A method to vary the contact number z}

In fact, all of our findings stem from a mistake. A marginally-jammed system near the jamming transition is quite abnormal in comparison to a typical solid: for a typical solid, different moduli ratio (such as the ratio between the shear modulus and the bulk modulus) is a constant; while near the jamming point, the shear modulus approaches zero, but the bulk modulus remains finite, making their ratio to diverge. At the very beginning, we aim to study this property in the jamming system, and we have developed a method to vary the contact number without changing the nodes' locations by gradually inflating all particles with the same percentage. Hence, more and more particles previously not in contact can touch each other, which corresponds to adding more and more bonds to our network, as shown in Fig.3. However, due to the carelessness, the particle's diameter is mistakenly set as its radius leading to a network with very high z. As a result, many cross bonds are existing in such a network. Thus, not only the graph topology change, but the system also goes beyond the typical packing scenario, as packed particles can only touch nearby neighbors and never penetrate through them to form intersecting bonds. However, the mechanical response of this network is amazingly similar to the typical solid, which is entirely affine. Owing to this mistake, we discover the affine transition related to graph topology in a packing derived network.