Advantages of Rydberg many-body systems in metrology
Published in Physics
Since the Rydberg atom has a large electric dipole moment [1], it responses strongly to a weak microwave electric field. This promising microwave measurement system has made a rapid development. Our project started as a simple test for recording the response of the Rydberg atoms under external microwave fields.
Inspired by the previous works on the non-equilibrium phase transition [2-3], we decided to test the response of a many-body system under the external microwave field. We thus wanted to see the difference of the many-body system (near the critical point of the phase transition) from the non-interacting system. Benefiting from the large interaction volume, as well as the strong many-body interaction, the Rydberg atoms near the phase transition point produce an avalanche phenomenon under very small perturbations of the Rydberg populations, which means that the system in the Rydberg many-body state amplifies the effect of the perturbation. It is interesting whether this amplifying effect works or not under the change of the external microwave field.
For this purpose, we started to focus on the metrology project of the Rydberg atoms near the phase transition point [5], using criticality as the resource to demonstrate the metrology [6-7]. The principle is described below.
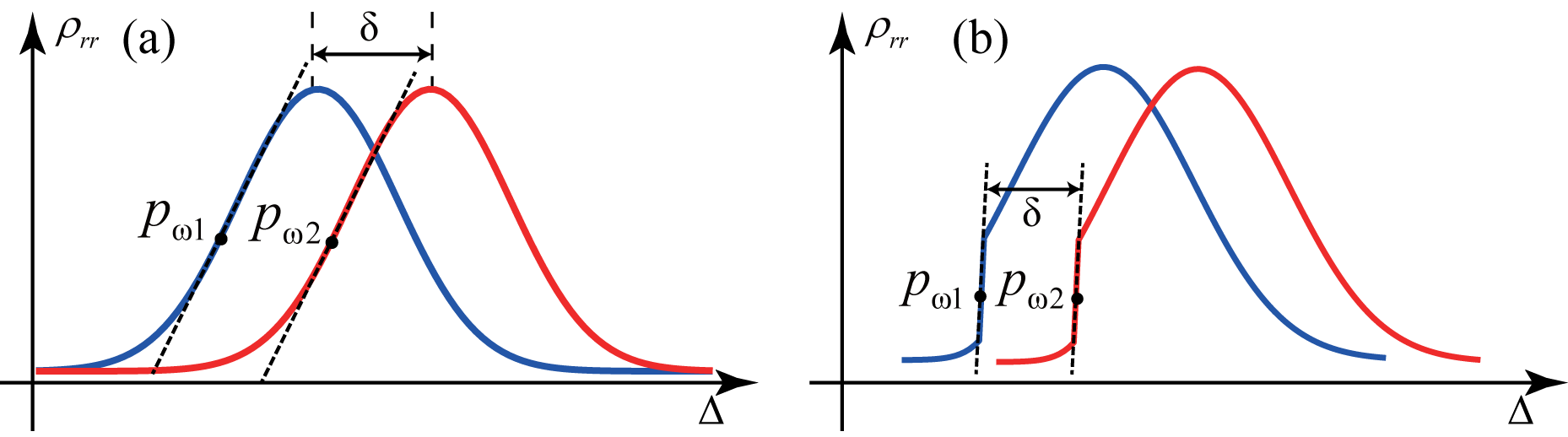
There is a non-equilibrium phase transition in the Rydberg many-body system, which is characterized by a steep edge on the transmission spectrum. This phase transition is caused by an avalanche of the Rydberg populations due to the interaction between the Rydberg atoms. In this case the number of Rydberg atoms changes significantly at the critical point. If a microwave electric field is applied, as shown in Figure 1, due to the Stark effect, the electric field will make the spectral line move.
For a moving spectral line, the movement of the steep edge is more obvious than the overall movement (the edge of the change in the field is more obvious) so the accuracy and sensitivity of the external electric field measured by the critical point are higher. The method of measuring the electric field using the critical point of the phase change is equivalent to a ruler with a finer scale compared to the method of measuring the electric field by using the overall movement of the spectral line, so the microwave electric field can be measured with greater precision.
Therefore, we take advantage of this property to further show the enhancement of the accuracy and sensitivity of the Rydberg atoms in detecting the microwave electric field near the phase transition point.
We found that an interacting many-body system can extract more information than an independent system, and even extract more information through long-time continuous measurements. The Fisher information shows a non-integer and power-law-dependent behavior of the measured time, which is caused by critical slowing down, so atomic dynamics deviate from the steady state near the critical point. The Fisher information is three orders of magnitude larger than in independent particle systems. In addition, we observed the detuning-dependent sensitivity, which is caused by the increasing strength of interactions near the critical point, as changes in detuning alter the Rydberg populations and therefore the intensity of the interaction. For non-interaction cases, even with rapid scanning in our experiments, the Fisher information is linearly dependent on time t.
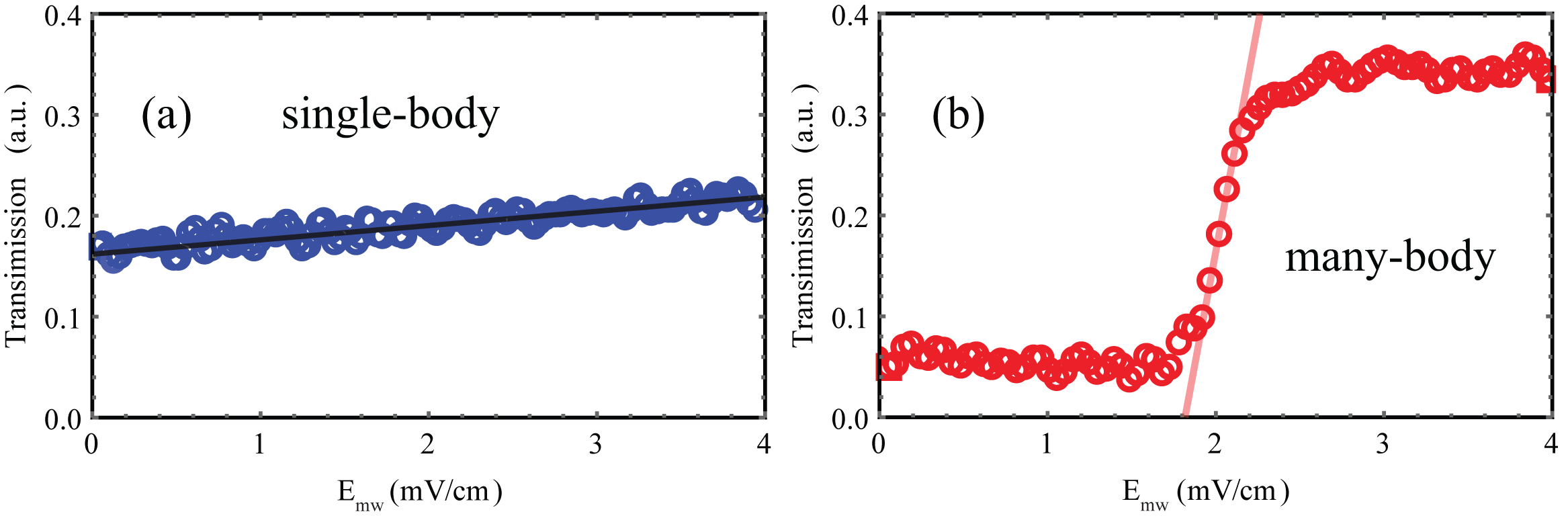
Figure 2. Transmission under different amplitudes of the MW field for the single-body case (a) and the many-body case (b).
Further, we show the transmission under the single-body case and the many-body case in Figure 2. In the single-body system, the transmission is not sensitive to the variance of the amplitude Emw. However, for the many-body condition, it is amazing that the response is highly sensitive to the field around values of Emw=2 mV/cm. Moreover, by considering multiple sequential independent measurements, the equivalent sensitivity is estimated to be 49 nv/cm/Hz^1/2.
Rydberg many-body system is a powerful platform, which would open the door towards the application of many-body effects in precision metrology.
Reference
- Saffman, T. G. Walker, and K. Mølmer, Quantum information with Rydberg atoms, Rev. Mod. Phys. 82, 2313 (2010).
- Carr, R. Ritter, C. Wade, C. S. Adams, and K. J. Weatherill, Nonequilibrium phase transition in a dilute Rydberg ensemble, Phys. Rev. Lett. 111, 113901 (2013).
- D-S. Ding, H. Busche, B.-S. Shi, G.-C. Guo, and C. S. Adams, Phase diagram of non-equilibrium phase transition in a strongly-interacting Rydberg atom vapour, Phys. Rev. X 10, 021023 (2020)
- D-S Ding, Z-K Liu, B-S Shi, G-C Guo, K. Mølmer and C. S. Adams. Enhanced metrology at the critical point of a many-body Rydberg atomic system. Nature Physics. (2022). https://doi.org/10.1038/s41567-022-01777-8.
- Zanardi, M. G. A. Paris, and L. Campos Venuti, Quantum criticality as a resource for quantum estimation, Phys. Rev. A 78, 042105 (2008).
- Gammelmark and K. Mølmer, Phase transitions and heisenberg limited metrology in an ising chain interacting with a single-mode cavity field, New Journal of Physics 13, 053035 (2011).
Follow the Topic
-
Nature Physics

This journal publishes papers of the highest quality and significance in all areas of physics, pure and applied.


Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in