Angular additional periodic phase manipulation for tunable deep-ultraviolet second harmonic generation
Published in Electrical & Electronic Engineering
Phase engineering of a wave function influences and determines the tendency and even results of physical processes, especially for efficient nonlinear optical frequency conversion. High conversion efficiency requires a strict phase-matching condition between the fundamental and harmonic electromagnetic, thus crystals without suitable birefringence and invertible ferroelectric domains were ruled out, which constrains the further development and application of nonlinear photonics in the broad spectral range, especially in the ultraviolet (UV) region. The novel strategy for the efficient tunable frequency conversion and universal nonlinear crystals are expected for dozens of years.
Recently, scientists in China proposed a novel and universal phase-matching strategy associated with phase manipulation, named as additional periodic phase (APP) phase matching. Such phase-matching condition is attributed to the artificial manipulation of the optical phase in the periodic ordered/disordered alignments. Compared with quasi-phase matching (QPM) with π-phase shift at the interfaces, APP phase matching allows continuous phase compensation with arbitrary non-centrosymmetric crystals (Fig. 1).
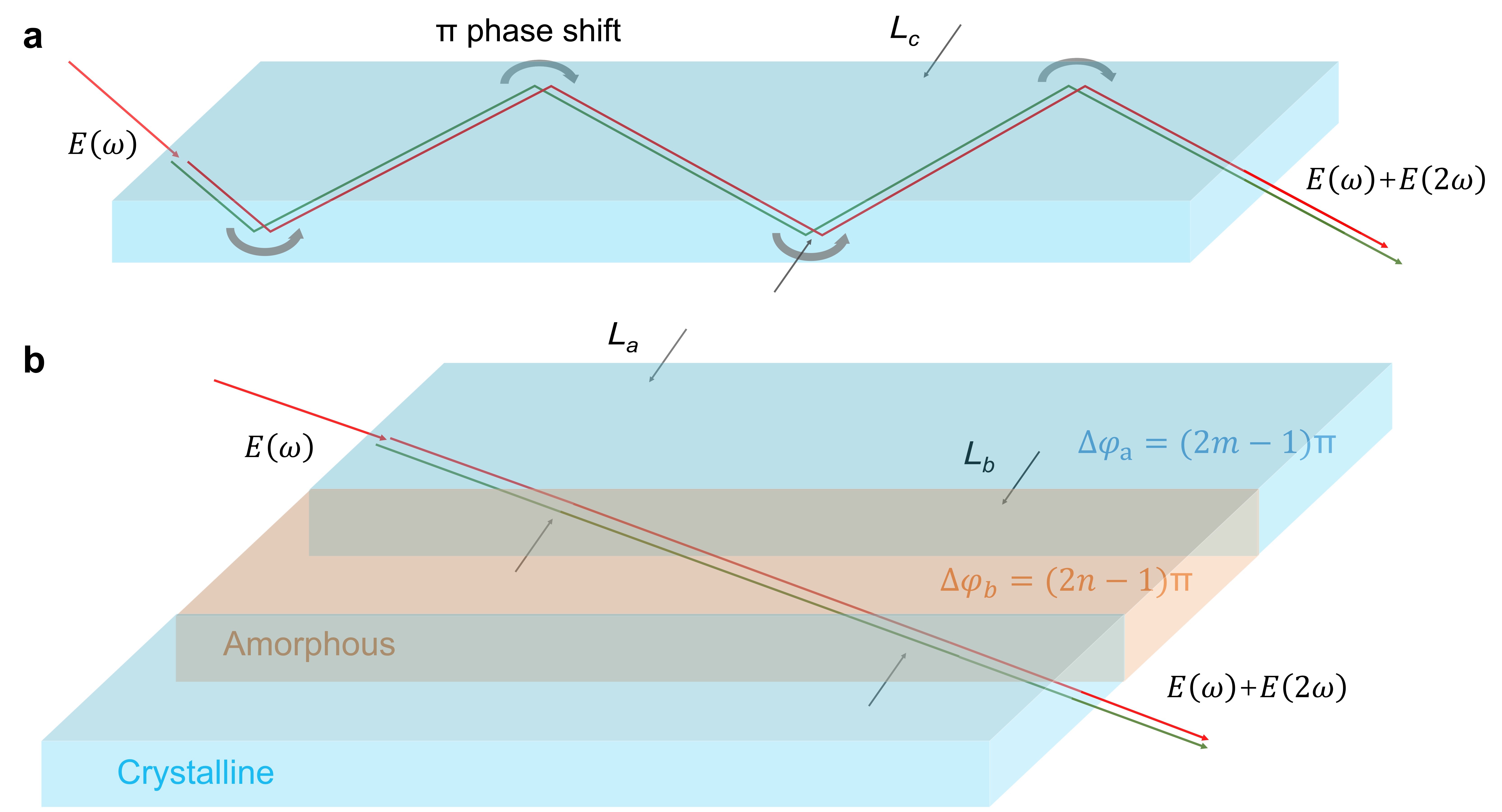
Fig. 1 Two different ways to provide phase manipulation. a Schematic of the traditional QPM method with a phase shift at the interfaces. b Schematic of the APP with a continuous phase change. In crystalline regions, a nonlinear optical process occurs with a phase difference , and then, in amorphous regions, phase manipulation operates with an APP .
Meanwhile, the light phase is related to its propagation length in the crystal, thereby giving rise to the possibility of the generation of tunable phase matching if the phase could be angularly engineered in angular APP phase matching, which has not been touched up to now and should be very important for the further applications of APP techniques.
In a new paper published in Light Science & Application, a team of scientists have theoretically investigated angular engineering of the additional periodic phase in APP phase matching. The key of angular APP manipulation is the effective optical path tunability, corresponding to the phase difference, by angle tuning to achieve the phase matching condition of with continuous phase compensation (Fig. 2). Moreover, large nonlinear coefficients can be employed under angular APP phase matching condition, which should be more flexible compared to the well-developed birefringence phase-matching condition. For many nonlinear optical crystals, especially for the ultraviolet nonlinear crystals, the birefringent phase-matching (BPM) condition Δk=0 is unavailable even with angle tuning for the crystals with too large or small birefringence. Similarly, QPM is also unavailable when there are no reversed ferroelectric domains. Therefore, limited by the refractive index dispersion, angle tuning is only suitable for specific crystals at typical wavelength ranges. Compared with other common deep-UV nonlinear optical frequency conversion technologies, angular APP strategy shows a great advantage in wavelength tunability, regardless of BPM or QPM techniques.
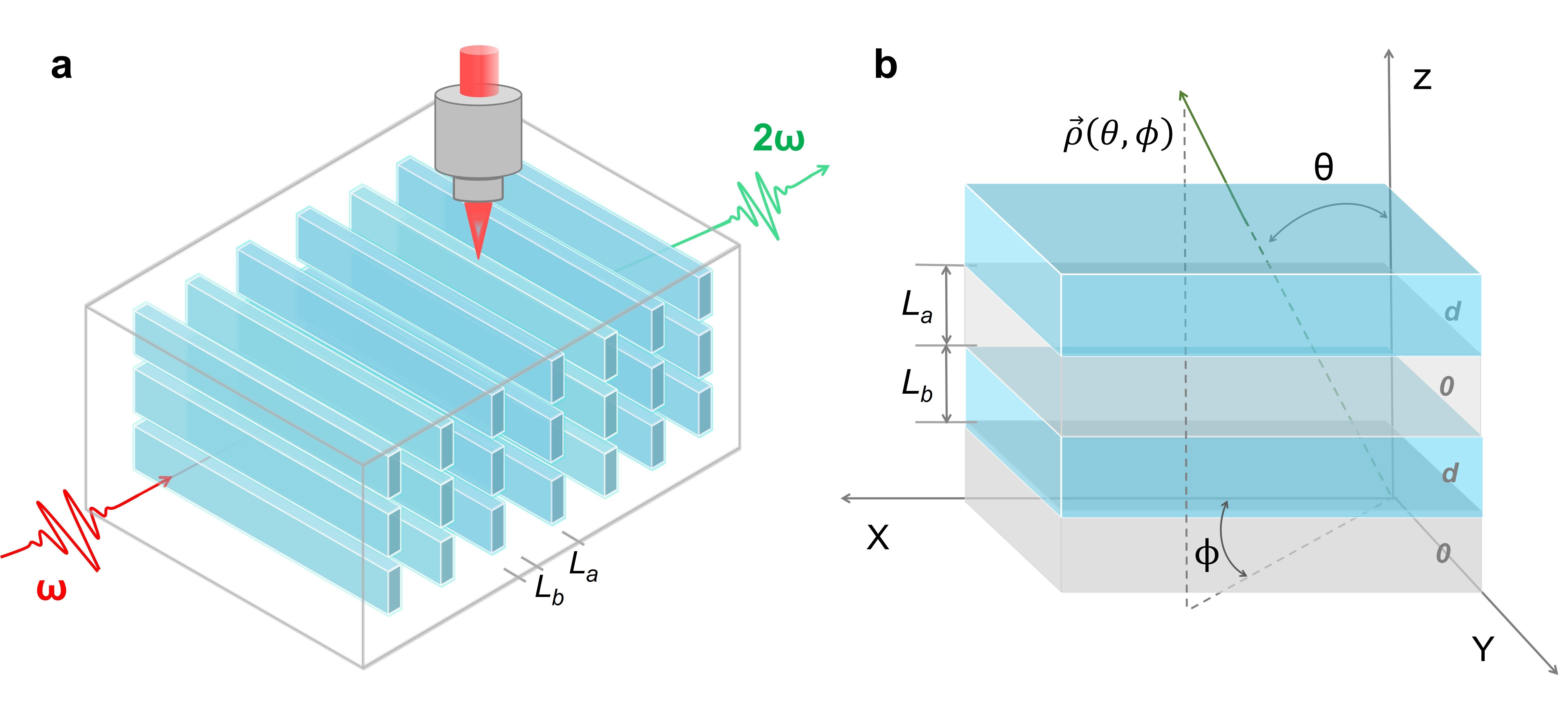
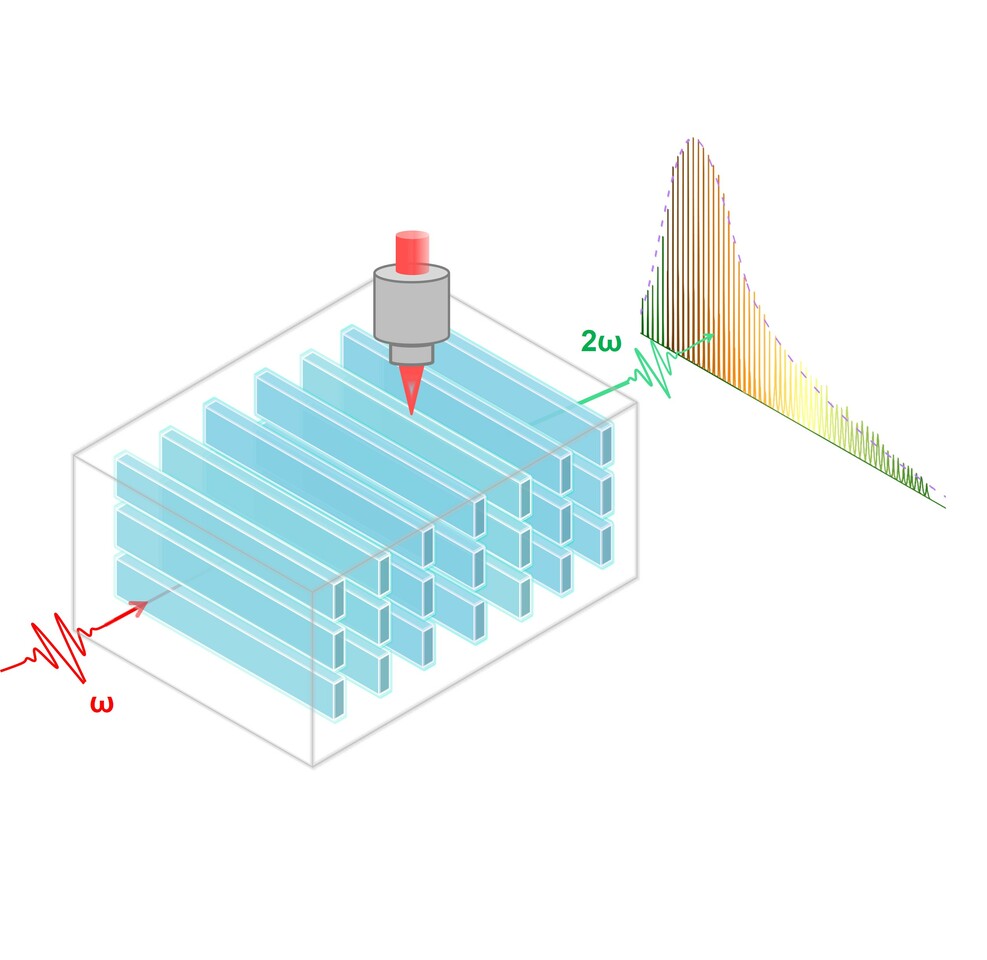
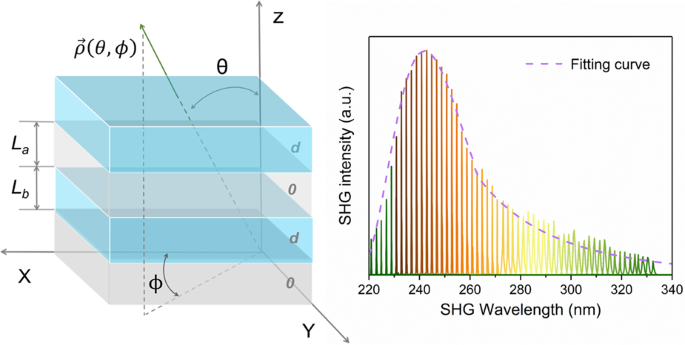
Fig. 2 Angular APP phase-matching engineering diagram. a Schematic of laser direct writing of APP gratings. Λ=La+Lb is the fabricated APP grating period, and La and Lb are the lengths of crystalline/amorphous regions of the crystal with second-order nonlinear coefficients of d/0, respectively. b APP gratings along the Z direction with the propagation direction of the interacting waves .
The angular APP phase matching was experimentally demonstrated with efficient tunable SHG (221-332 nm) covering almost the entire deep-UV spectral range with an APP quartz crystal (Fig. 3b). In addition, all possible phase-matching types are also originally simultaneously achieved with the participation of phase variation induced by the distribution of the grating period within a certain range. What’s more, the azimuth angle tuning can be employed not only to select nonlinear coefficients, but also to manipulate the polarization output in different phase matching types (Fig. 3c), which should be very difficult or unavailable in traditional phase-matching conditions due to the dispersion of refractive index, thus could be further applied in relevant scientific fields, such as laser-induced periodic surface structures, laser-scanning nonlinear optical techniques and even some quantum entanglement fields.
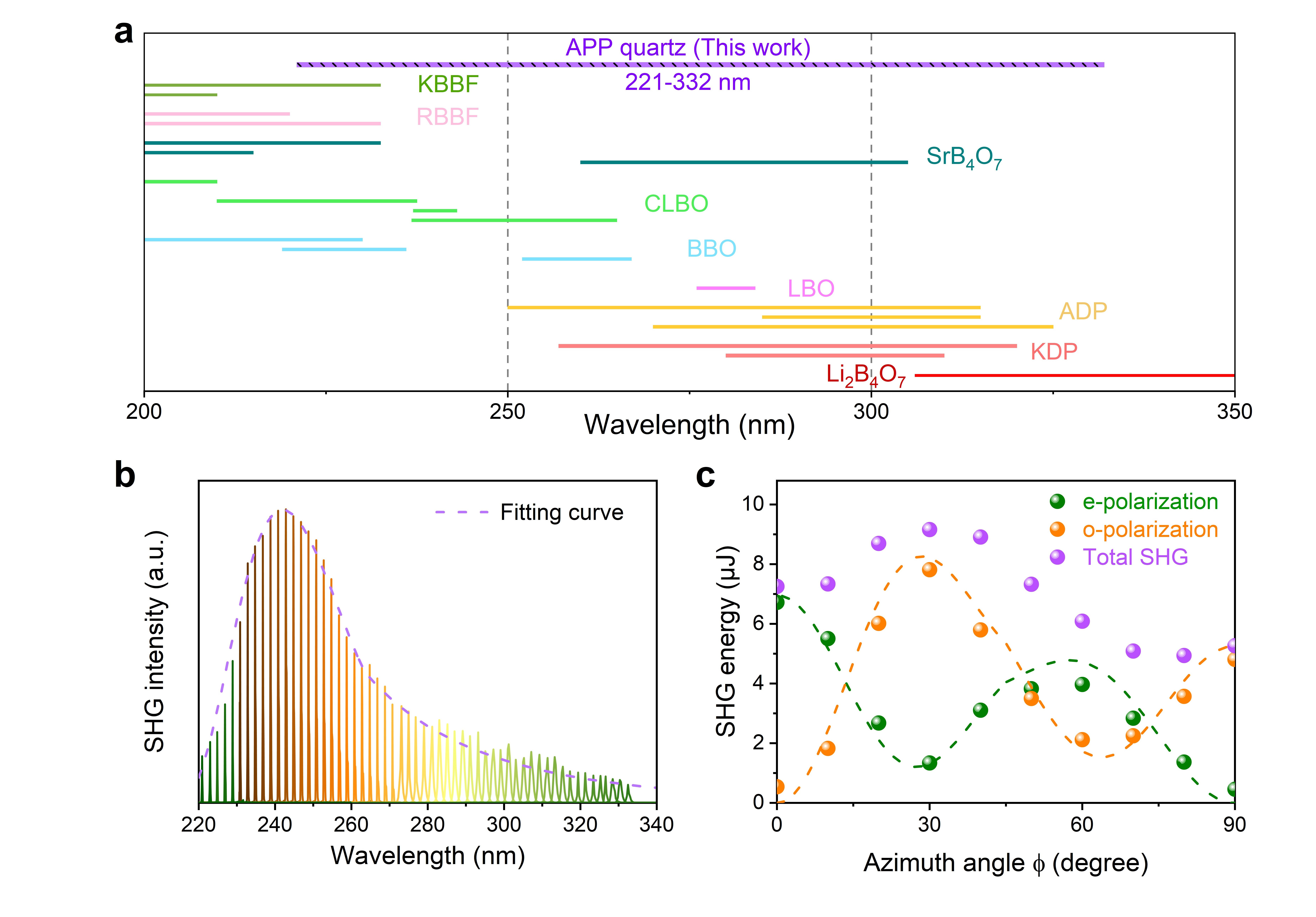
Fig. 3 Experimental demonstration of angular APP phase matching with APP quartz. a Comparison of the tunable spectral region of this work with those of common nonlinear optical crystals in the deep-UV (200-350 nm) range. b SHG signal intensities at different wavelengths from 221 nm to 332 nm. c Calculated (curves) and experimental (dots) SHG intensities for ordinary and extraordinary light at 250 nm with azimuth angle tuning from 0° to 90°
In conclusion, this work has demonstrated angular APP manipulation for widely tunable phase-matched SHG and experimentally demonstrated it in an APP quartz crystal. Through the introduction of angular manipulation, efficient SHG was realized in an APP quartz with a tunability of 111 nm in the UV range and all possible phase-matching types were simultaneously realized. Angular APP phase matching should provide a new route for nonlinear optics and thus will be key to opening the door for realization of tunable deep-UV lasers. This novel and practicable work should be further development of APP phase matching and could inspire further studies in nonlinear optics, photonics and even physics.
Follow the Topic
-
Light: Science & Applications

A peer-reviewed open access journal publishing highest-quality articles across the full spectrum of optics research. LSA promotes frontier research in all areas of optics and photonics, including basic, applied, scientific and engineering results.
Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in