Artificial intelligence for improved fitting of trajectories of elementary particles in dense materials immersed in a magnetic field
Published in Physics
Understanding the behaviour of subatomic particles in dense materials and magnetic fields, particularly in the context of particle detectors, is vital in high-energy physics (HEP) [1]. The development of imaging detectors, which lead to the reconstruction of particle tracks in three dimensions, needs accurate particle flow reconstruction and the measurement of primary particle properties. Standard methods for track fitting, such as Bayesian filters, are based on Monte Carlo techniques. These methods incorporate knowledge about particle propagation through a medium and use likelihood calculations to estimate particle states. However, these methods often require simplifications and approximations due to the complexity of the problem.
Artificial intelligence, specifically deep learning, can offer a promising solution to improve particle reconstruction. Based on artificial neural networks, deep learning algorithms can effectively extract complex features from multidimensional data. In the field of HEP, deep learning has been successfully applied to tasks such as particle classification, semantic segmentation, and regression [2]. However, directly extracting high-level physics information from raw detector signals can be challenging. Therefore, an alternative approach is proposed, which combines deep learning with traditional particle flow methods. This approach involves a chain of analysis steps, including matching detector signatures, defining complex objects like tracks, and fitting tracks to reconstruct particle kinematics. The last step, track fitting, is crucial and is typically performed by Bayesian filters. The reconstruction performance depends on the detector design and the prior knowledge of particle propagation in the detector. Deep learning can address the challenge of parameterising a high-dimensional space and improve reconstruction performance by explicitly utilising neural networks for this purpose.
While deep learning has been explored as an alternative to Bayesian filtering in various applications, its application in particle tracking has been limited to connecting detected hits to form particles rather than fitting the detected hits to approximate the actual particle trajectory. The article proposes using recurrent neural networks (RNNs) and Transformers, borrowed from natural language processing, for fitting particle trajectories. These neural networks, resembling Bayesian filters with hyper-informative priors, have the potential to improve the accuracy and resolution of particle trajectory reconstruction significantly. Figure 1 compares the performance of the three methods, indicating that the Transformer and the RNN outperform standard techniques.
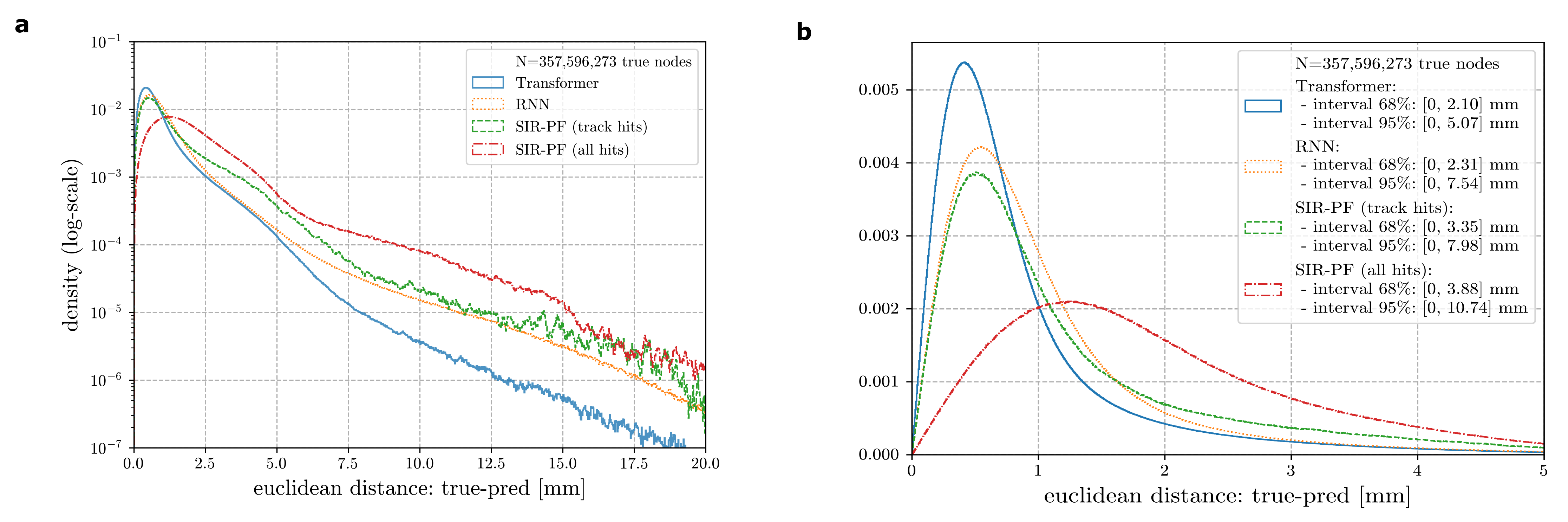
The accuracy of the trajectory fitting dramatically affects the precision of physics measurements, making the neural network reconstruction better capture the curvature due to the magnetic field compared to the Bayesian filters, thus helping improve the charge identification accuracy. This enhanced resolution allows for improved detector performance or more compact designs. The momentum resolution for protons is also better with the neural networks, especially the Transformer. The particle identification capability is also enhanced with the neural networks, as demonstrated by the more accurate reconstruction of the energy deposited by protons and improved particle identification for various particles and energies. Some of these results are shown in Figure 2.
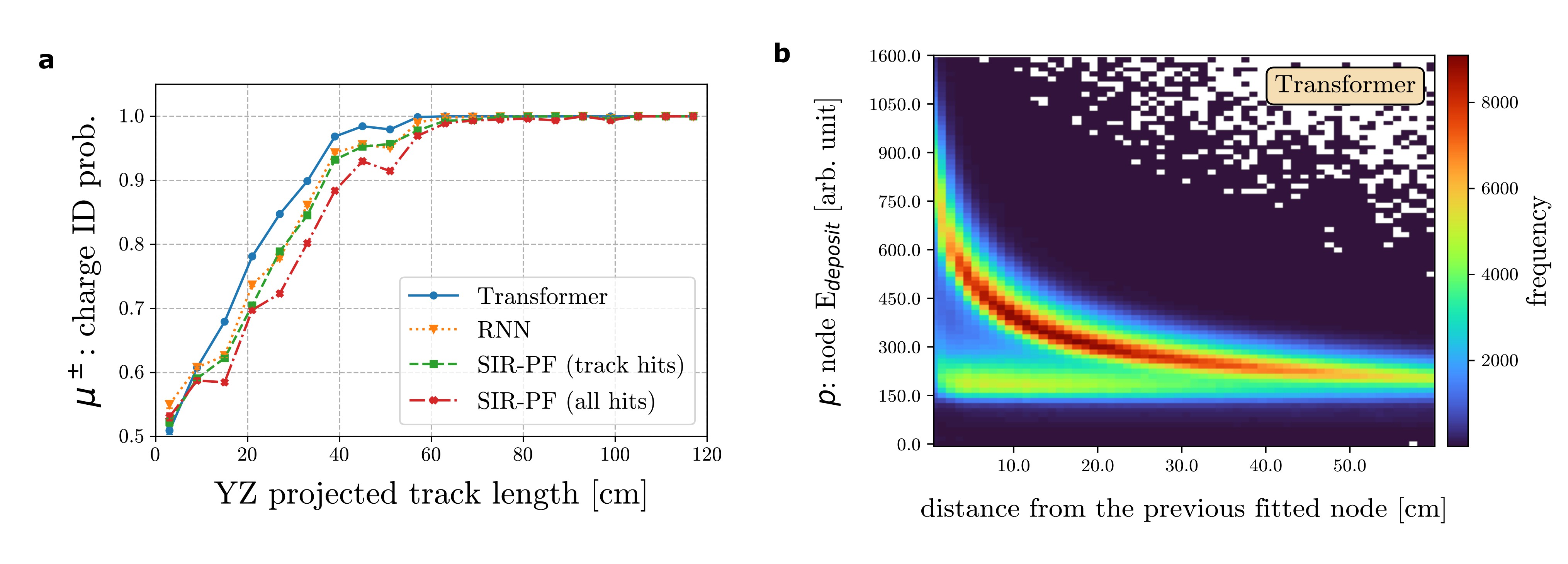
We believe this approach is a milestone in artificial intelligence applications in HEP and can play the role of a game changer by shifting the paradigm in reconstructing particle interactions in the detectors. The prior, which is consciously built from the modelling of the underlying physics from data external to the experiment, becomes as essential as the real data collected for the physics measurement. De facto, the prior provides a strong constraint to the "interpretation" of the data, helping to remove outliers introduced by detector effects such as from the smearing introduced by the point spread function and improving the spatial resolution well below the actual granularity of the detector.
This work is focused on physics exploitation in particle physics experiments. However, the developed AI-based methods can also fulfil the requirements in applications outside of HEP, as long as one has a valid training dataset. One example is proton computed tomography [3] used in cancer therapy, where scintillator detectors are used to measure the proton stopping power along its track in the Bragg peak region to precisely predict the stopping position of the proton in the human body. Future improvements to the developed NNs may involve investigating the effects of varying noise levels and multiple tracks in the detector volume, as well as the direct computation of the node stopping power from the track, i.e., the combined fitting of both the node particle position and energy loss.
References
[1] F. Hasert, H. Faissner, W. Krenz, J. Von Krogh, D. Lanske, J. Morfin, K. Schultze, H. Weerts, G. Bertrand-Coremans, J. Lemonne, et al., “Search for elastic muon-neutrino electron scattering,” Physics Letters B, vol. 46, no. 1, pp. 121–124, 1973.
[2] A. Radovic, M. Williams, D. Rousseau, M. Kagan, D. Bonacorsi, A. Himmel, A. Aurisano, K. Terao, and T. Wongjirad, “Machine learning at the energy and intensity frontiers of particle physics,” Nature, vol. 560, no. 7716, pp. 41–48, 2018.
[3] R. W. Schulte, V. Bashkirov, M. C. Loss Klock, T. Li, A. J. Wroe, I. Evseev, D. C. Williams, and T. Satogata, “Density resolution of proton computed tomography,” Medical Physics, vol. 32, no. 4, pp. 1035–1046, 2005.
Follow the Topic
-
Communications Physics

An open access journal from Nature Portfolio publishing high-quality research, reviews and commentary in all areas of the physical sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Higher-order interaction networks 2024
Publishing Model: Open Access
Deadline: Feb 28, 2026
Physics-Informed Machine Learning
Publishing Model: Hybrid
Deadline: May 31, 2026




Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in