Bottom-Up Cell Design: Starting From The Simplest Self-Replicating Subsystems
Published in Bioengineering & Biotechnology
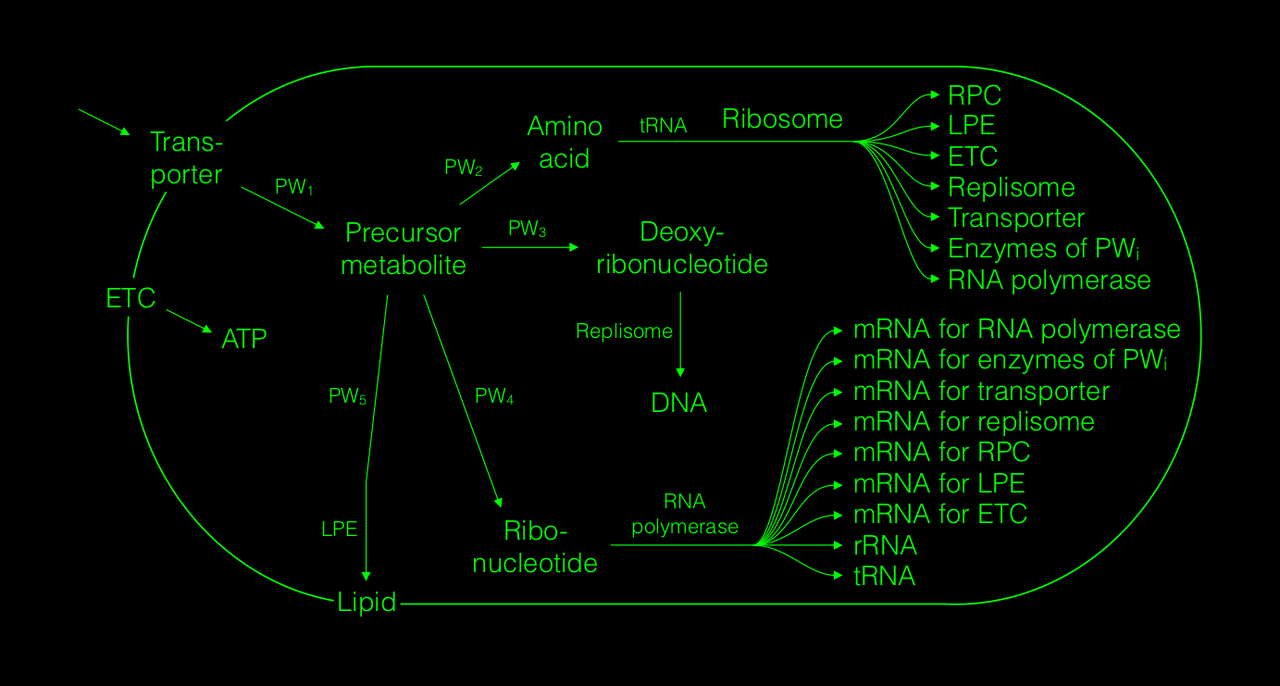
One of the grand goals of synthetic biology is to become able to design and construct cells ab initio, bottom up, from their basic building blocks (as opposed to just tweaking the already existing cells). For this, a good understanding is needed about how the cells function. Studying the biological cells in a lab is, certainly, one key aspect of building that understanding, but it has also serious limitations: experiments tend to be slow, costly, difficult, and usually constrained by practicalities into exploring only a small region of the large space of theoretically possible cells. Therefore, it is highly desirable to complement the experiments with a theoretical framework of how the cells function, as well as with computational modelling and design tools for exploring the fundamental possibilities and limits of cells.
The creation of such a set of theoretical and computational tools is exactly the goal that we have set out to achieve. It is certainly possible to approach this goal in different ways, and different scientists have indeed taken different routes towards it. Some build cell models that rely heavily on detailed physical modelling — this can give a high level of realism, but is also computationally very difficult and can be too detailed for seeing the higher-level general functional principles of a cell. Others build models that include an abstraction of some of the key parts of the cell, such as metabolic networks, but leave out some other fundamental aspects, such as cell geometry. Our preference has been to try to include all fundamentally important subsystems of a cell, but at the same time to keep the level of abstraction sufficiently high to maintain the comprehensibility of the models as well as make the models easily computable on a personal computer, and, additionally, to make the framework sufficiently flexible so that the level of detail, abstractness and complexity can be changed as necessary.
So, over many (tens of) years we have been developing such a theoretical framework of the functioning of bacterial cells, complemented with computational models based on that theory, and now the first paper of an upcoming series about this work has been published. It is based on the fundamental concept of self-replication, starts with minimal biological self-replicators — ribosomal proteins — and builds a family of 10 models of self-replicating proto-cells (or cellular subsystems) by adding other significant cell components that support the ribosomes.
The modelling framework itself is flexible enough to allow reaching the complexity of full genome-scale cell models and even bacterial consortia, but in the interest of clarity and soft introduction, the most complex model of the first paper is still one that is highly simplified and easily graspable, representing a bacterial proto-cell growing on minimal medium:
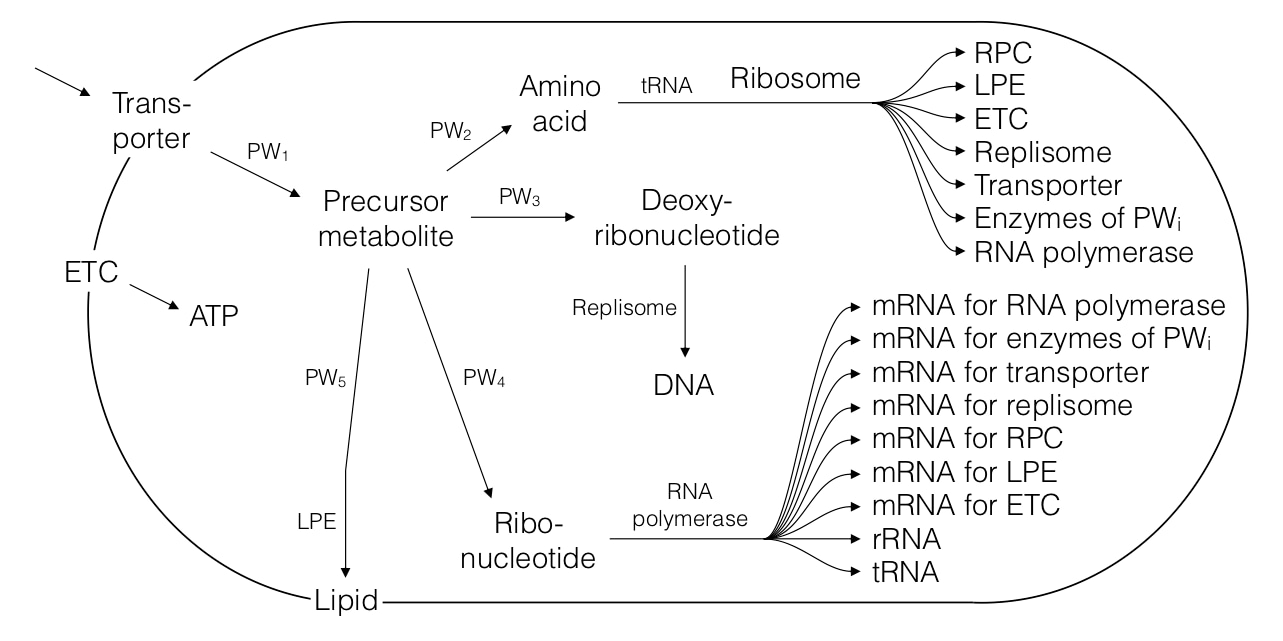
All provided proto-cell models allow for a full analysis of the numbers and properties of all included cell components and processes in a steady state of the cell. For the interest of, again, clarity and soft introduction, the currently published paper focuses the analysis mainly on one of the fundamental parameters of self-replication — the doubling time. We show that doubling times of the analysed proto-cells, ranging from simplest replicators up to those reaching the size of E. coli, increase rather with the number of different cell component species than with the total numbers of cell components, and also that the way how different types of cell components influence the doubling time depends on the types of relationships between those cell components and ribosomes:
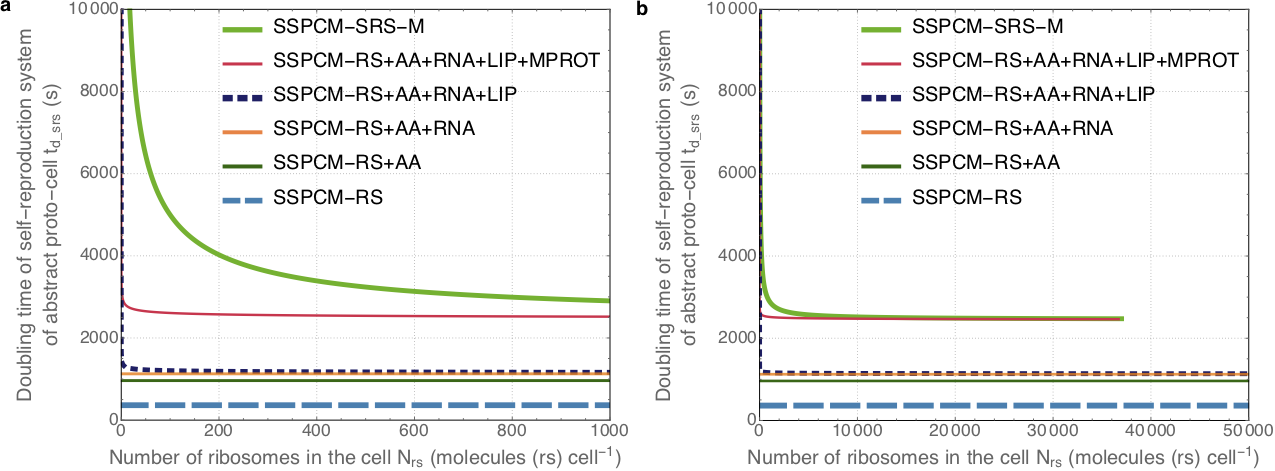
This understanding of how and why the doubling time, and thus also the growth rate, of cells can be insensitive to the total numbers of cell components is crucial for cell design, because this insensitivity allows for a lot of freedom in optimising cell contents and size for our goals without losing the benefits of high growth rates and stability.
For a full explanation of the figure, as well as for a short overview of the models, see the main text of the paper. A much more detailed and comprehensive description of each model and the calculations is given in the supplementary materials, so we highly recommend to take a look at those as well.
Overall, we hope that the modelling framework we have developed helps to uncover and illuminate the fundamental principles of cells, and, after we present in upcoming publications also the more advanced model families of this framework, provides also a solid foundation and tools for computational cell design.
Follow the Topic
-
npj Systems Biology and Applications

An online Open Access journal dedicated to publishing the premier research that takes a systems-oriented approach and encourages studies that integrate, or aid the integration of, data, analyses and insight from molecules to organisms and broader systems.
Related Collections
With Collections, you can get published faster and increase your visibility.
Next-Generation Mammalian Cell Bioprocessing: Systems Biology, Synthetic Biology, and Beyond
Publishing Model: Open Access
Deadline: Mar 15, 2026
Systems mechanobiology
Publishing Model: Open Access
Deadline: Mar 28, 2026
Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in