Collective response to individual actions in social systems
Published in Social Sciences

One of our main research lines at the Complex Systems Group of Universidad Politécnica de Madrid is the study of user influence in online communities. In particular, we are interested in the ability of individuals to generate spontaneous responses, measuring their collective impact. For example, in Twitter an influential user would be one that gets a lot of retweets. However, a user can be very retweeted because she sends many moderately popular messages or because she sends few highly popular messages. Who of these two users would be more influential? To take that into account, we characterize user influence with the efficiency metric, which relates the individual activity (A), or number of actions of an individual (original tweets in the case of Twitter), and the collective response (R), or number of reactions she triggers on others (obtained retweets in the case of Twitter). This measure is inspired in the well-known physical concept of engine efficiency, which is the ratio of the work we get from the engine and the energy invested to make it work. Accordingly, the efficiency (η) is defined as η=R/A. This way we consider both the individual effort to spread information and the influence achieved through that effort.
In a previous work of the group the distribution of efficiency was studied in Twitter data, finding that it adopted a universal shape in every conversation (see figure below). Two approaches were considered to reproduce the efficiency distribution and explain this ubiquity. On the one hand, the empirical distribution was fitted to functions that visually resembled the shape of the distribution, but those ad hoc fits do not tell us why the efficiency distribution adopts precisely that shape. On the other hand, an agent-based model was developed to mimic the retweeting dynamics. But the ubiquity of the distribution made us think that, just like the universality of the normal distribution can be explained by the central limit theorem; that is, due to the variable under study being the sum of many underlying random variables that can be considered independent, the recurrent shape of the efficiency distribution may also emerge, not from the specific dynamics of Twitter, but from a simpler universal underlying mechanism.
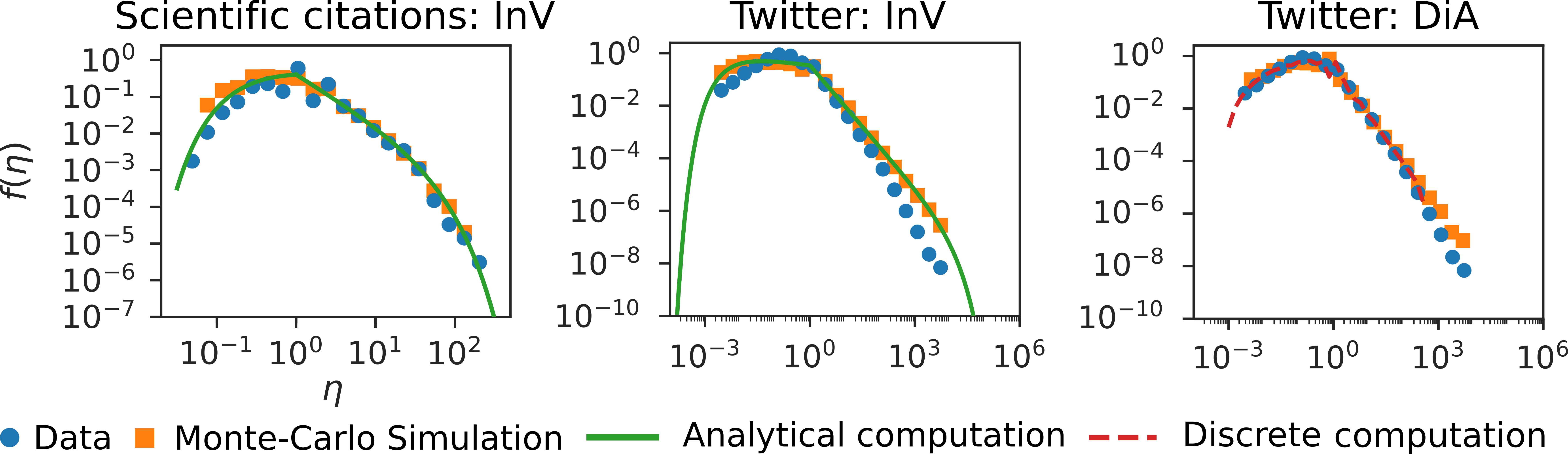
Efficiency distribution for a Scientific Citations dataset and for a Twitter dataset.
With this idea in mind, we developed the Independent Variables (InV) model, which is based in considering A and R as independent random variables. If a complex causal mechanism is responsible for the efficiency distribution, the shape of the efficiency distribution according to the InV model should be very different from the original one. But as can be seen in the figure above (orange squares and green line of the middle panel), it stays practically the same. From these computations, we conjectured that if such a simple model can explain the shape of the efficiency distribution, we would find similar results in other social systems.
To test that hypothesis, in our current work we studied the efficiency distribution in 29 datasets of three different social systems: Twitter, Wikipedia and the Scientific Citations network, verifying that the distribution presents a similar shape across the different scenarios. From these results, it is clear that the ubiquity of the shape of the efficiency distribution can be explained by the efficiency being the ratio of two random variables that can be considered independent.
However, in the paper we develop two more sophisticated theories that correct the small discrepancies between the InV model and the data. In the Identical Actors (IdA) model, a dependency between R and A is introduced in a parsimonious way and the system reacts to the stimuli of every actor in the same way; in the Distinguishable Actors (DiA) model the reaction of the system depends on the features of the individual that stimulates it. This last model fits the Twitter data remarkably well when the number of followers of the users is used as their distinctive feature. However, despite its simplicity, the InV model still performs very well when there is a large number of variables determining the response of the system, as their relative effects balance each other out. That is the case for the Scientific Citations network (see figure above), where R (the number of citations) depends on many factors, from the quality of the manuscript or journal, to the field of research, the reputation of the authors, their institutions, etc.


Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in