Recent advances of quasi-2D materials have also opened up new horizons in physics of disordered materials. Indeed, many phenomena relevant to electrical transport, such as the electron-electron interactions renormalization, Anderson localization, and phase fluctuations, are boosted in low dimensional structures significantly. In particular, detrimental influence of the lowered dimensionality combined with the disordered potential has been observed in amorphous as well as highly crystalline 2D superconductors.

Disorder can also give rise to a remarkable improvement in superconductivity figures of merit. It controls the interplay between the superconductive pairing and long-range phase coherence. Strong disorder potential gives rise to the spatial inhomogeneity of a superconducting state, which enhances the local pairing correlations and superconducting gap. On the other side, stronger disorder can enhance phase fluctuations, thereby reducing the superfluid density (stiffness) and suppressing superconductivity on the global scale. One, therefore, expects there exists an optimal degree of inhomogeneity, at which the superconductivity enhancement and the superconducting critical temperature are maximal.

Random impurities and defects in otherwise ordered materials can thus be regarded as a tool to control superconducting characteristics of materials, a design element to engineer superconductors with desired functionalities. Most theoretical investigations are restricted to models describing spatially uncorrelated disorder, which are furthermore analyzed using perturbation expansion methods. In real systems, however, the disorder is almost never completely random. The inhomogeneities are often structured and are characterized by the long-range spatial correlations.

Here we investigate the influence of such long-range correlations on the superconducting state at zero temperature. We investigate superconducting properties of a 2D superconducting sample with spatially correlated disorder. The results show that such correlations change statistical properties of the Cooper pairing and enhance multi-fractal features of the order parameter. As the result, global superconductivity becomes more robust with respect to the disorder strength.

The calculations are done using the model of the structural disorder where the spatial correlations of the disorder potential in the inverse space obey the power law

S_V(q)∼q^-α

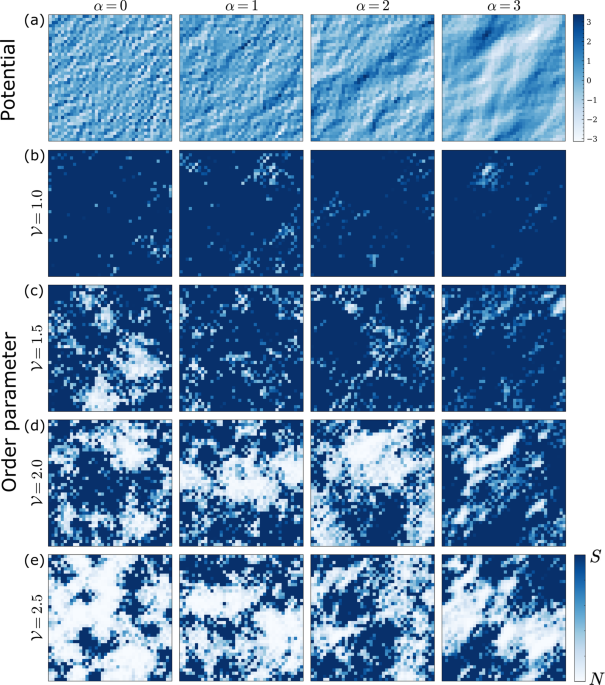
in the limit of small q. The power exponent α determines the correlation degree. Using this model for the random potential we solve the microscopic equations numerically without further approximations and obtain the order parameter profile, typical examples of which for different values of the correlation degree and the disorder strength are shown in Fig. 1. 

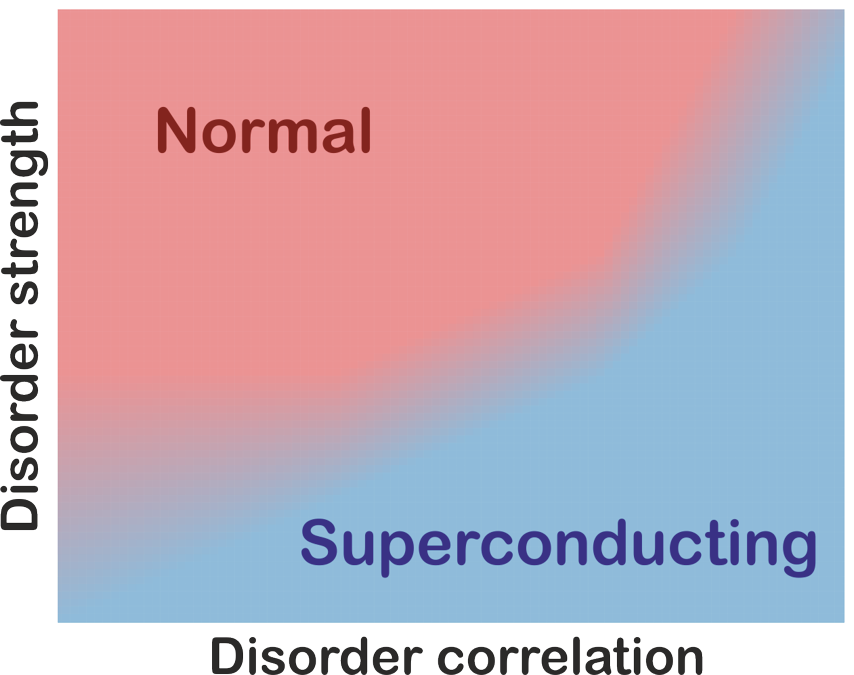
Main results of the work are summarized in Figure 2 showing superconductive (S) and normal (N) phases in the plane Correlation degree – Disorder strength. This phase diagram highlights a general tendency that the correlations inhibit the destructive influence of disorder on superconductivity.  

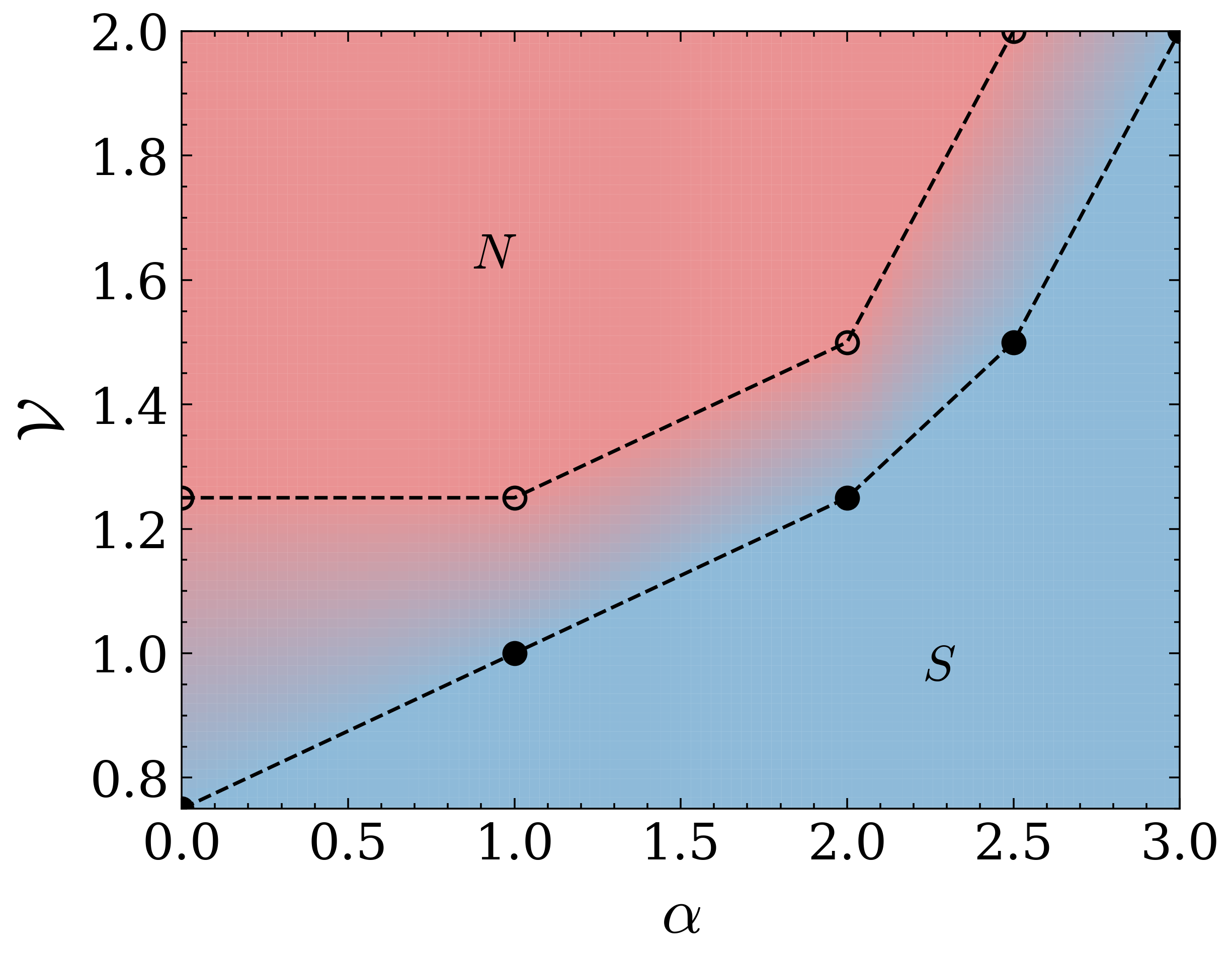
The results demonstrate that spatial correlations in the disorder potential is a very important factor. It changes essential superconductive properties and, therefore, cannot be ignored for disordered materials. Furthermore, manipulating disorder correlations when possible can be used as another design parameter to alter superconducting characteristics and to design materials with desired functional properties.