Non-linear differential equations (DEs) describe complex systems in nature, such as fluid dynamics, climate modeling, and general relativity, to mention a few. While linear equations are widely applicable, non-linear equations often arise in systems where interactions or feedback loops create more intricate and unpredictable behaviours. Yet, in most cases, analytic solutions are either impossible or highly complex, necessitating the use of numerical methods to provide solutions. With the advent of deep neural networks, particularly Physics-Informed Neural Networks (PINNs), it has become increasingly feasible to solve complex DEs more efficiently. An added layer of complexity arises when the goal is to solve inverse problems, where the objective is to infer unknown parameters or functions within a system based on available data, such as initial or boundary conditions.

PINNs, how they work, and multi-head technique

PINNs are neural networks used to solve DEs. As in their name, they are informed on the physics behind the DEs they are solving. This means the equations guide the training process rather than being solved through traditional discretization. The PINN acts as an approximate solution function (taking as input a number "x" and returning as output "f(x)"), which changes along training to iteratively minimize the residuals of the DEs when evaluating them at this approximate solution.

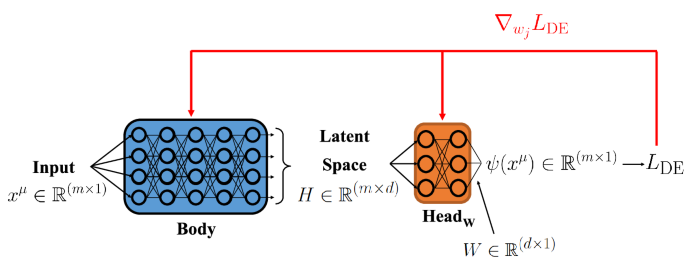
A wide range of architectures and constructions exist in the use of PINNs. We study the "multi-head" technique, where several neural networks share a common "body", which is attached to different "heads" that solve one specification of a family of DEs. In this way, the shared body learns general features across each of the individual problems specific to each head. Once trained, this shared body can be reused to transfer knowledge to new or more extreme regimes, where the DEs become more complex and harder to solve. This transfer not only improves accuracy in these challenging settings but also accelerates convergence, since the network starts from a body already tuned to relevant features rather than from scratch. We study this technique in three different DE problems (the flame equation, the Van der Pol oscillator, and Einstein Equations in the context of holography, being the last an inverse problem).

In a way, the body can be seen as a higher-dimensional space encoding many possible variations of the DEs, and the head as the projection of this space into a lower dimensional one that acts as a solution to a specific variation.

The idea of this work: Unimodular Regularization inspired by General Relativity

In the context of high-dimensional spaces and hypersurfaces, and inspired by general relativity and the underlying differential geometry, we started wandering if concepts like the curvature of the spacetime metric field, the differential volume of this field (determinant of the metric), the Riemann and Ricci curvatures, and others, could be computed for the hypersurface encoded in our PINN "body".

As it turns out, we could and did, and observed hypersurfaces with extreme curvatures in certain limits of the DEs (limits that span independent variable values, boundary or initial conditions, and parameters within the equations), where the finding of approximate solutions became more challenging. In a heuristic way, the more challenging and less accurate the solutions were, the higher the curvature of the body hypersurface was. Moreover, using then this highly-curved body for transfer learning (TL) failed to provide solutions for more extreme regimes and the TL procedure broke. We then developed the Unimodular Regularization (UR) technique. This technique is applied during the training of the body; it forces the body to solve the equations while keeping the differential volume of the hypersurface (this is, the determinant of the metric tensor) small at all points. Its name is inspired by an alternative theory to General Relativity called Unimodular Gravity, where the determinant of the metric tensor is set to unity. When applied to our setup, the UR technique reduces the amount of variability between different points of the body's hypersurface once the training is finished. We found that using the "regularized body" (trained with UR) for TL yielded more accurate solutions for more extreme regimes than the "standard" (no UR) body, and even gave reasonable solutions for the most extreme cases where the procedure without UR was unable to find a solution.

Applications and future work

This research helps improve the efficiency of PINNs used in a multi-head and transfer-learning manner to solve differential equations, improving the accuracy of solutions, and unlocking the ability of obtaining them in some extreme regimes. This has potential applications in any field of science where the non-analytical resolution of DEs is required, such as physics, mathematics, biology, economy, and many others. In future work, one may want to improve the efficiency when computing the metric field of the hypersurface that encodes the information in the PINN body. Also, we would like to generalize the case to partial differential equations, which is in principle straightforward. Finally, we would like to test the Unimodular Regularization technique on other problems, specially of inverse nature, where PINNs can be extremely useful as opposed to traditional numerical methods.