Optomechanical Sensors

Optomechanical sensors represent a cutting-edge frontier in precision measurement and quantum technology [1]. These sensors are capable of achieving unprecedented levels of sensitivity in detecting the macroscopic motion of a mechanical device, such as a deformable membrane or mirror. At the heart of these systems lies the interaction between light and mechanical vibrations, where tiny disturbances of the mechanics get imprinted on light, leading to measurable optical signals; see Figure 1 for an artistic illustration. A remarkable application of optomechanical sensor technology is exemplified by LIGO (Laser Interferometer Gravitational-Wave Observatory) [2], which employs an interferometer featuring massive suspended mirrors situated at its endpoints to measure the minute displacements caused by gravitational waves—deformations in spacetime generated by cataclysmic cosmic events, such as black hole mergers.

As with all measurements, systematic and intrinsic noise sources pervade the optomechanical system. For instance, even after cooling down the mechanics and reducing incessant Brownian motion, the mechanical signal inferred from the optical fields will be noisy due to intrinsic quantum fluctuations of the electromagnetic field (or shot noise). Shot noise can be reduced by increasing the laser power of the field, however at some point, radiation pressure from the strong laser—induced by momentum transferring from photons of the field to the mirror and back—becomes significant, leading to backaction noise. By delicately balancing backaction and shot noise, we can approach the Standard Quantum Limit (SQL) of the optomechanics, which is best measurement sensitivity we can hope to achieve with "classical" resources; see solid black curve in Fig. 1(b) for a depiction. Fortunately, it has been known for quite some time that we can go beyond the SQL by reducing the optical field fluctuations via quantum squeezing [3], an idea which is being deployed in LIGO's current observing run [4]. Unfortunately, squeezing does not permit better on-resonance sensitivity, however squeezing can significantly increase the measurement bandwidth of the detection system, allowing us to surpass the SQL away from resonance; see Fig. 1(b) for a depiction. This is fantastic, but we scientists are an insatiable lot. The lingering question is thus: Can we do more?

Entanglement-Enhanced Sensing

In a landmark paper in 2018, Zhuang et al [5] introduced a novel and remarkably simple  paradigm to measure field amplitudes (or more generally, "bosonic displacements") in a distributed setting. In this context, many sensors are spatially distributed and jointly influenced by some unknown field whose amplitude we would like to measure. Quite miraculously, the authors demonstrated that the optimal detection configuration (assuming no losses) involves distributing a squeezed vacuum  to the sensors, performing homodyne detection on the output fields, and employing joint classical post-processing—e.g., coherently combining the measurement results. An illustrative depiction of this concept is on the cover artwork accompanying this article. This serves as a prime example of harnessing multipartite entanglement to significantly enhance the capabilities of sensing technologies; i.e., once the squeezed vacuum is distributed, the modes become entangled and the noises become globally (but not individually) suppressed.

Recently, my collaborators and I have applied these fundamental insights to practical receiver designs consisting of microwave cavity sensors [6] and optomechanical sensors as described in our recent publication featured in Communications Physics [7]. A proof-of-principle demonstration of this entanglement-enhanced sensing with an optomechanical array of two sensors was recently realized in a shot-noise dominant setup [8], thus paving the way for futuristic optomechanical sensor arrays operating deep in the quantum regime.

These fundamental results in distributed quantum sensing were begging for a "killer app". So we talked to our high-energy physics friends and found that researchers worldwide are on the hunt for elusive dark matter and innovative detection methods are desperately desired.

On the Hunt for Dark Matter

Dark matter is an essential component of our universe—constituting about 25% of universal mass budget—yet no one has a clue what it is made of. Nevertheless, theorists are ingenious creatures who have concocted many plausible  "dark matter candidates", such as axions, dark photons etc., which typically lie outside the standard model of particle physics, consisting of quarks, electrons, photons etc. These candidates may couple very weakly to standard model particles, allowing us to observe them with, e.g., optomechanical devices [9]. For these models, a significant practical challenge to address is the fact that the candidate mass and the coupling constant to the standard model are generally unknown over an extensive range (spanning, for instance, ~70 orders of magnitude for the mass!), implying a vast parameter space to explore.  Researchers—notably the eloquently named Windchime collaboration [10]—have also ambitiously proposed the direct-detection of dark matter via  its gravitational interaction with an array of mechanical devices; the challenge here though is that gravity is notoriously weak and thus a large array, as well as ultra-sensitive measurements, are required. It is clear that large-scale precision sensing is crucial in the hunt for dark matter.

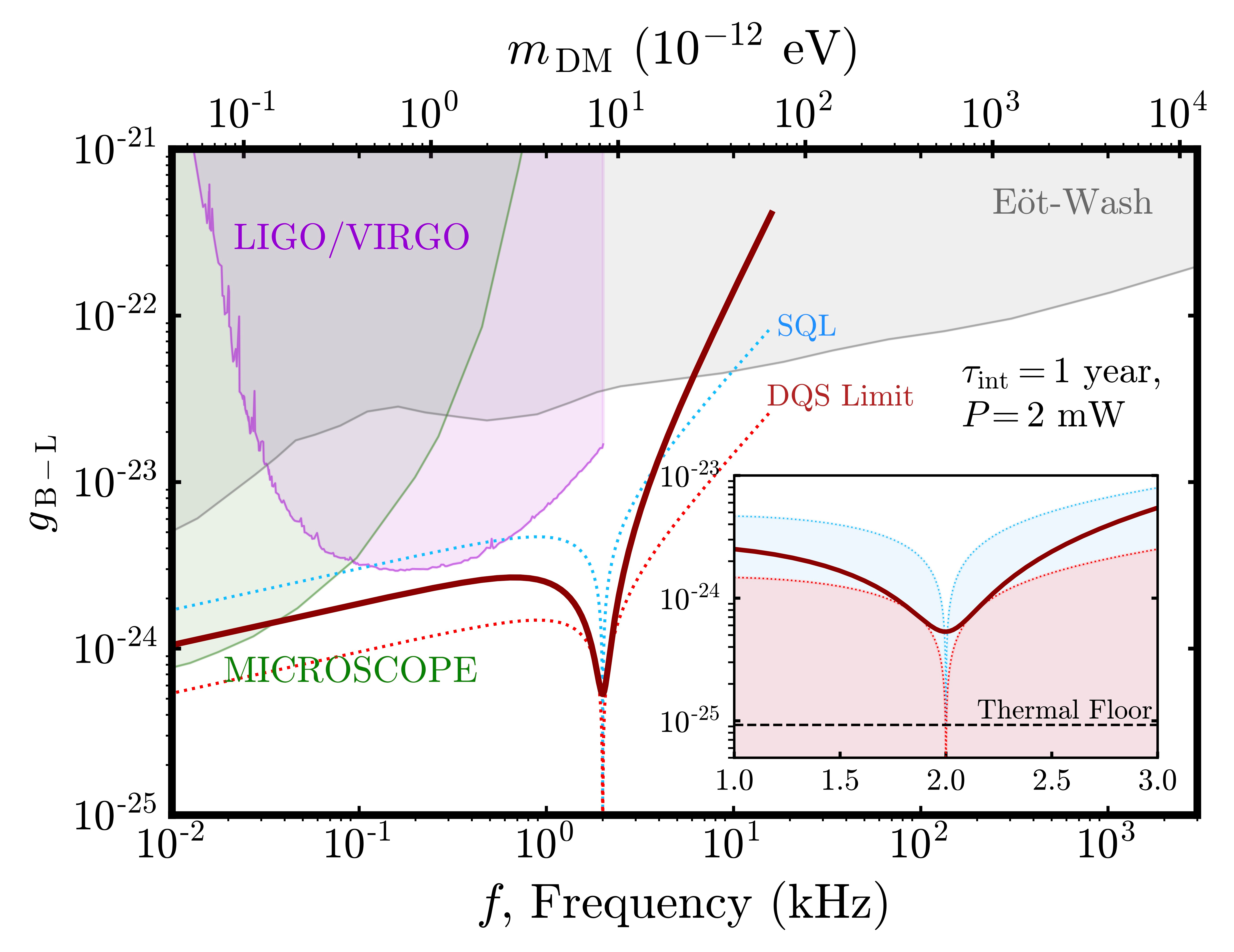
This is where we can play our quantum tricks to gain an advantage. As we have recently elaborated [7], interrogating an array of mechanical sensors with distributed squeezed light can greatly enhance force sensitivity (relative to a classical setup) by increasing the measurement bandwidth and, consequently, improving the scan time in a search for dark matter. In Fig. 2, we present sensitivity projections for a hypothetical dark matter wave coupling (via "B-L coupling") to an array of mechanical membranes (10 sensors here) that we can interrogate with a distributed squeezed laser (10 dB of squeezing here). Notably, we can dip below the SQL by leveraging a single squeezed vacuum source distributed across the entire array, regardless of the number of sensors in the array. This achievement represents a remarkable reduction in the resources required to exceed the quantum limits of optomechanical devices. The sensitivities and resource-saving strategies proposed here could prove invaluable for direct-detection proposals aiming to employ millions of mechanical sensing devices [10].

Closing Thoughts

Our work on distributed quantum sensing with applications to potential dark matter searches [7] epitomizes a collaborative endeavor that draws upon the expertise of numerous theorists and experimentalists. The theoretical contributions encompass a diverse range of skills spanning quantum information, quantum sensing, and high-energy/dark matter theory. Meanwhile, our experimental friends are well-versed in the design and operation of mechanical membranes and have exquisite expertise in quantum optics, including the generation of squeezed light. The fruitful and fluid exchange of ideas within the group, largely facilitated by our joint affiliations with the SQMS center, led us to identify a remarkable application for the fundamental results in quantum sensing that may have otherwise gone unnoticed. 

We anticipate that our research will have a profound impact on the design of futuristic dark matter detectors, pushing the boundaries of sensitivity and precision. Beyond the realm of dark matter, we envision broader implications for mechanical-sensing applications, such as subterranean imaging, accelerometry, and magnetometry, among others.

References 

1. Barzanjeh, Shabir, et al. "Optomechanics for quantum technologies." Nature Physics 18.1 (2022): 15-24.
2. Laser Interferometer Gravitational-Wave Observatory, www.ligo.caltech.edu/. Accessed 18 Sept. 2023.
3. Caves, Carlton M. "Quantum-mechanical noise in an interferometer." Physical Review D 23.8 (1981): 1693.
4. Tse, M. E., et al. "Quantum-enhanced advanced LIGO detectors in the era of gravitational-wave astronomy." Physical Review Letters 123.23 (2019): 231107.
5. Zhuang, Quntao, Zheshen Zhang, and Jeffrey H. Shapiro. "Distributed quantum sensing using continuous-variable multipartite entanglement." Physical Review A 97.3 (2018): 032329.
6. Brady, Anthony J., et al. "Entangled sensor-networks for dark-matter searches." PRX Quantum 3.3 (2022): 030333.
7. Brady, Anthony J., et al. "Entanglement-enhanced optomechanical sensor array with application to dark matter searches." Communications Physics 6.1 (2023): 237.
8. Xia, Yi, et al. "Entanglement-enhanced optomechanical sensing." Nature Photonics (2023): 1-8.
9. Carney, Daniel, et al. "Mechanical quantum sensing in the search for dark matter." Quantum Science and Technology 6.2 (2021): 024002.
10. Attanasio, Alaina, et al. "Snowmass 2021 White Paper: The Windchime Project." arXiv:2203.07242 (2022).