With the rapid advances in developing quantum technologies, there has been much attention put on how to experimentally prepare and manipulate quantum entanglement in a system with many particles.  A simple way to verify the presence of entanglement is to estimate the global state of the multipartite system. However this quickly becomes impractical because the number of parameters we need to estimate scales exponentially with the number of particles.

This has led to various approaches for certifying global entanglement from the partial knowledge of certain subsets of a few particles. Such information could be a collection of marginal density operators for a few subsystems, or it could be data obtained from the measurement outcomes of individual particles. 

Still, we may be more interested in more than just the entanglement at the global level. For instance,  when running an algorithm on a quantum computer, we might want to confirm that a particular group of qubits becomes entangled. But this is not something that we can determine just from knowing that the global state is entangled.

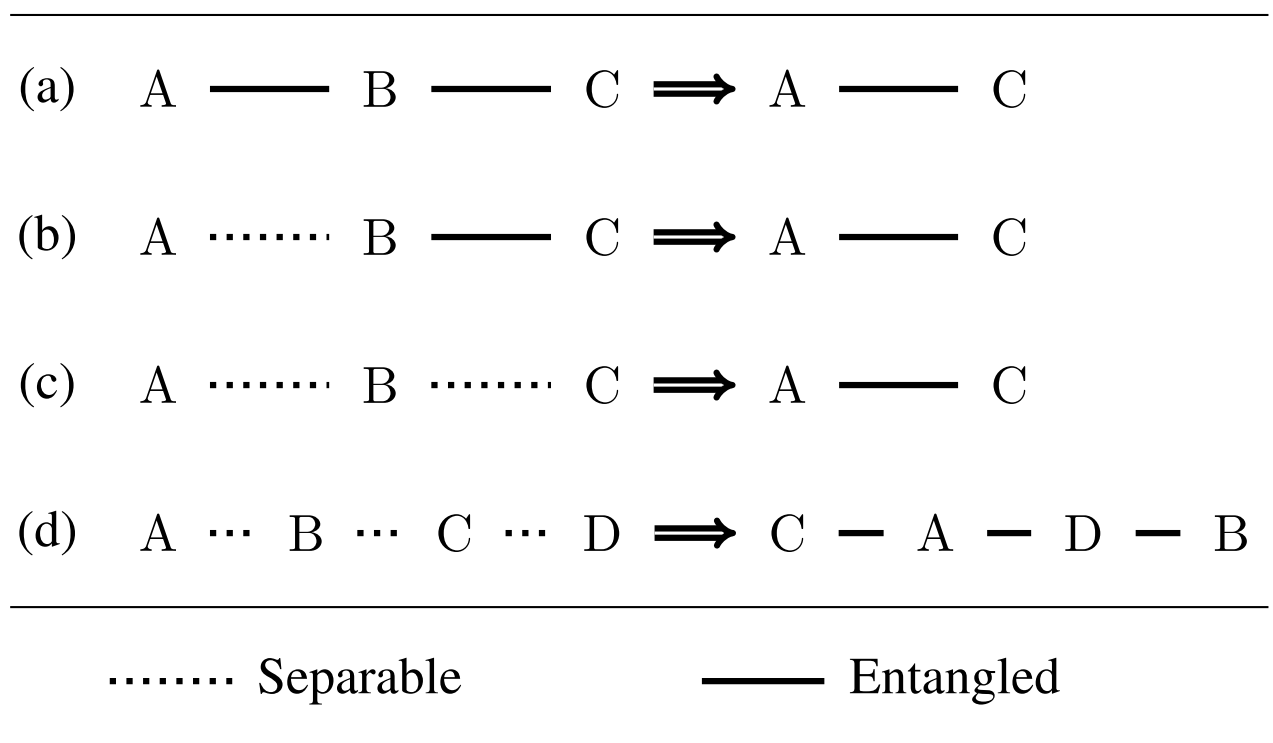
To accommodate the many possibilities, we formulate what we call the entanglement transitivity problem: Given a set of marginal quantum states, can we certify that the reduced state of a target subsystem must be entangled? 

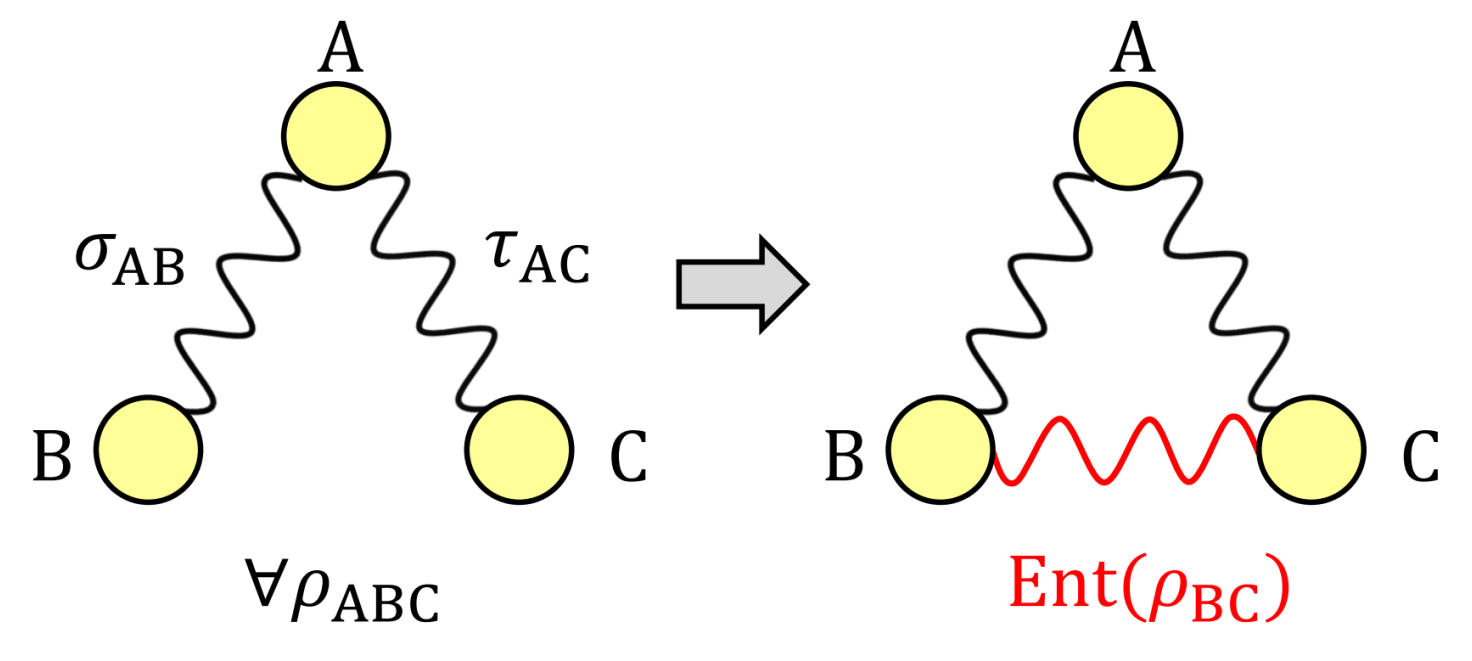
To see why we call it transitivity, consider a simple example involving three particles A,B, and C. Suppose that the pair AB is in some entangled state σ_AB and the pair AC is in entangled state τ_AC. If from this information we can conclude that the pair BC must be entangled for any possible global state for ABC, then we say that σ_AB and τ_AC exhibit transitivity in the marginal subsystem BC.

Note that we can choose any subsystem with unknown reduced state to be the target subsystem, and this includes the global system. We can even consider multiple target subsystems. More importantly, note that what is required is a set of compatible marginal states. It is actually not necessary for these marginal states to be entangled. It is only the target state that is required to be entangled.

To detect entanglement, the standard method is to employ an entanglement witness. Formally, an entanglement witness is a linear function W such that for all separable (non-entangled) quantum states S, we have W(S) ≥ 0, and for at least one entangled state E, we have W(E) < 0. In practice, the function W corresponds to measuring some observable ω. If we find that the expectation value of ω is negative, this suggests the presence of entanglement Otherwise, the result is inconclusive because the quantum state might still be entangled but this cannot be detected by the specific witness used.

We show that for a given entanglement witness W, we can certify transitivity in some target subsystem T by solving the following optimization problem:

Given a set Λ of compatible marginal states for a system S with target subsystem T⊆S, maximize W(ρ_T) over all ρ_S, where ρ_T is the reduced state of target subsystem T when ρ_S is the global state of S.

If we obtain a negative optimal value, this means that for every global state ρ_S compatible with the marginal states in set Λ, the witness always detects some entangled state in the target subsystem.

In our paper, we use the above method of certification to describe examples of transitivity involving an arbitrary number of qubits and tripartite systems for any finite local Hilbert space dimension. From numerical calculations, we also observe that transitivity is a generic phenomenon for any two bipartite marginal states of pure tripartite qudit state that is picked uniformly at random. Most interestingly, we find that there are collections of separable marginal states that imply that the marginal state in some other subsystem must be entangled.