Introduction & Background

In the alternative investments business (funds, funds of funds investing in start up or small - middle enterprises) where available ESG-related data are rare / very scarce or even  not available at all, investment's targets may be ESG-assessed via questionnaire. 

Questionnaire are seen as valid qualitative instrument (ex. due diligence questionnaires - DDQ) for qualitative assessments but not yet seen as valid qualitative source of information.  Actually an open question, without currently a unique answer in the corporate world, is how to quantitatively measure questionnaires results in this field and if/how to  produce an ESG sustainability / ESG risk probability based on the questionnaire results.

The article provides an answer to this question, developing a structured quantitative framework to score and interpretate the results of an ESG questionnaire from a very general perspective, providing also empirical data (companies ESG Assessed) in small measure but looking forward to produce available statistical points.

Behind-the-scenes

The approach followed by the author (please look into the poster for a synthesis and in the articole itself for details) is to start with an abstract mathematical approach thinking the questionnaire and its answer as a QxA cartesian set and the score value as a set function symilar to a signed measure (even if it's real set function nature is the relevant one). Seeing the score as a set function it's possible to rethink it as a probability,  mapping it in 0,1 (via a sigmoid  function in the article but it is valid  for a general probabilistic mapping). Both ESG  Score and Probability will have specifics (these are valid topics to follow up) however they already provide the quantitative framework to develope an ESG metric answering the "open question" the Business community has  and also deriving results to abilitate the usage of questionnaires for scoring purpposes. 

Summary of main results

The article introduces a new mathematical approach that uses modern mathematics to answer the interrogative, considering scoring a questionnaire the result of a real value set function / similar to a measure  on the answer space and linking the score value to an ESG-risk probability via a score-probability mapping with a probabilistic interpretation.  

The methodology introduced for these specific types of questionnaires, being abstractly defined, is applicable to other questionnaires type where Y/N answer are the possible outcomes, it is however been developed for ESG questionnaire.

The article shows some empirical results of the methodology developed and opens to a broaden application both empirical (submitting questionnaires to more available companies) and theoretical digging into the possible quantitative implication of the approach introduced leveraging from the parallelism introduce between a questionnaire to be scored and the building of the real valued set function s as it would be a random walk, with the score value advancing when the answer is ESG-positive and stepping back (or staying still) when the answer is ESG-negative.

Theoretically the article describes answering a questionnaire like a score function  walk where the measure value s increase or decreases (Y/N) based on the questions’ answers. 2 models are introduced one where positive answer get +1 and negative -1  (s is signed) and a model where positive answers get +1 and negative answers 0 (s is always positive).  The question relevance is taken into account by a rank r ∈ (1,2,3) and each answer has a contribution of type (±1 e^r ), with an exponential behaviour able to intercept questions with differenct degrees of impact actually low  (r=1), middle (r=2) and high (r=3).  The summed score s is mapped into a probability by a 1 parameter sigmoidal  of type  1/(1 + e^-x  ) function that is chosen among other probability mappings for its limited growth underlying assumptions and deep probbailistic interpretation. Also, a distance between scores is finally derived. The model tries to introduce a rigorous approach in scoring the ESG questionnaire embracing the opportunity to have a normalised value (probability) to compare each company measurement and a company in time.

Empirically the questionnaire is applied to few (4) companies and future publication will bring more empirical points / scored companies.

Follows up and topic to discuss.

A set of topics introduced in the article are open to follows up in both theoretical and empirical application. A (non complete) list: 

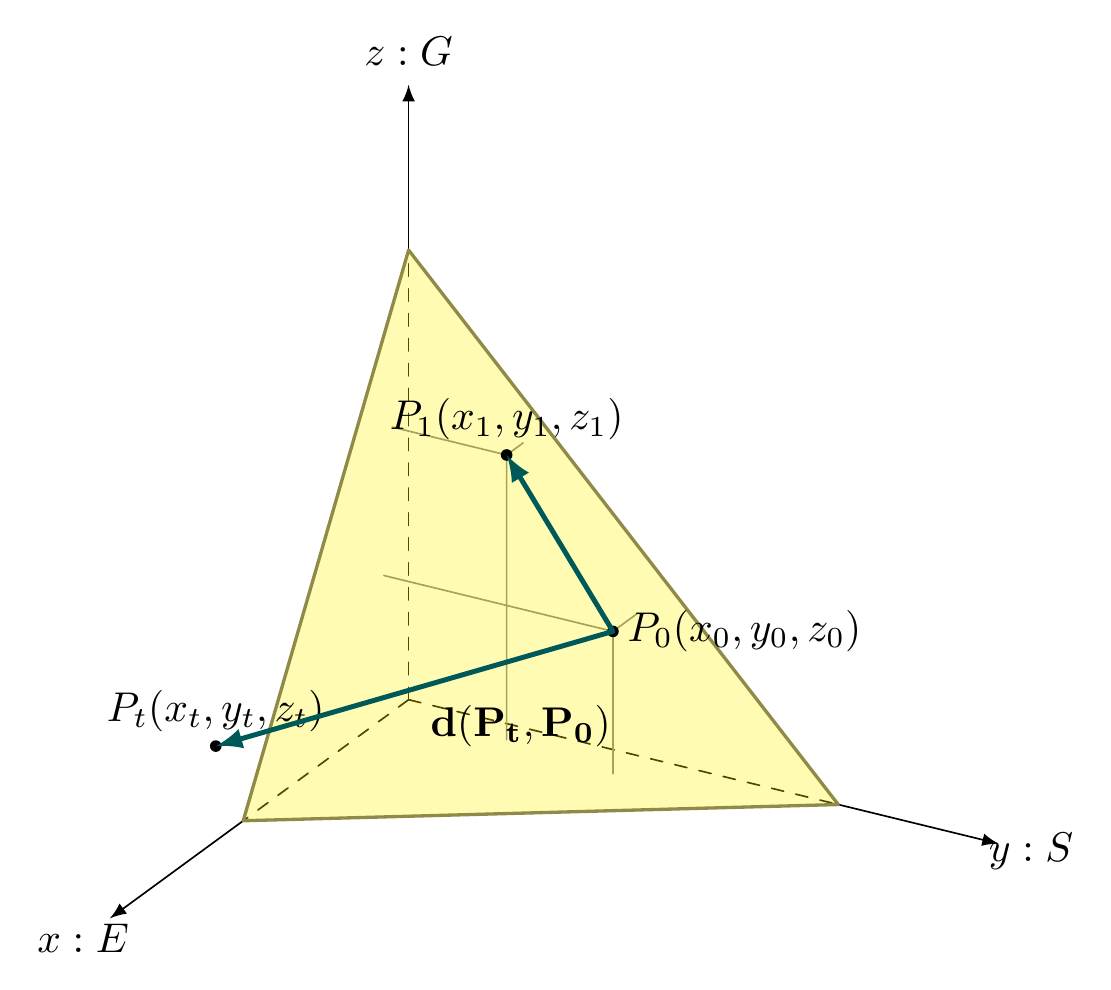
1. The idea of having a set function on the c & a probability associated with it,  has been merged with a “dimensional” view where each E,S,G dimension is assimilated to an x, y , z euclidean space with therefore a dynamic (temporal evolution of P) . It turns out the opportunity  to measure the distance between P on different times  for 1 company and P between different companies (in general P between different questionnaires). This line of theory had been  only sketched suggesting to acknowledge that the dynamical system for P in the E,S,G space should be investigated usyng metric spaces and dynamical systems techniques.

2. The choice of the Sigmodial function to map the set function score value into a probability  (0,1) has deep roots, however it's not the unique choice & a general investigation on probability mappings is definetly an avilable line of research.

3.  The notion of score as a set function can be extended and made more rigorous taking from measure theory and its implication.  An even higher degree of abstraction can be introduced above the idea of a questionnaire answer space.  The process of making abstract a theory is very valuablee and opens to new and unexpected results. Same for the idea of a (random) walk as building up the final score value is a line of research. 

4. Empirically a set of questionnaire  will be submitted to more companies and real statistical data will be driven in order to assess evolution of the ESG score & probability as well  avareges values among business classes and cases. 

5. Finally Survey of acutal corporate world questionnaire scoring is definetly valuable as it seems that in ESG (and not only) questionnaire are yet understimated as assessment instrument while lacking quantitative perspective that the author belive the present article has helped to retrieve and support.

Conclusions

The idea of having a set function on the answer space and a probability associated with it has been merged with a “dimensional” view where each E,S,G dimension is assimilated to an x, y , z space with therefore a dynamic (temporal evolution of P) and therefore possibility to measure the distance between P on different times and P between different companies (in general P between different questionnaire). This line of theory had been sketched suggesting to acknowledge that the dynamical system for P in the E,S,G space should be investigated.

Pictures.

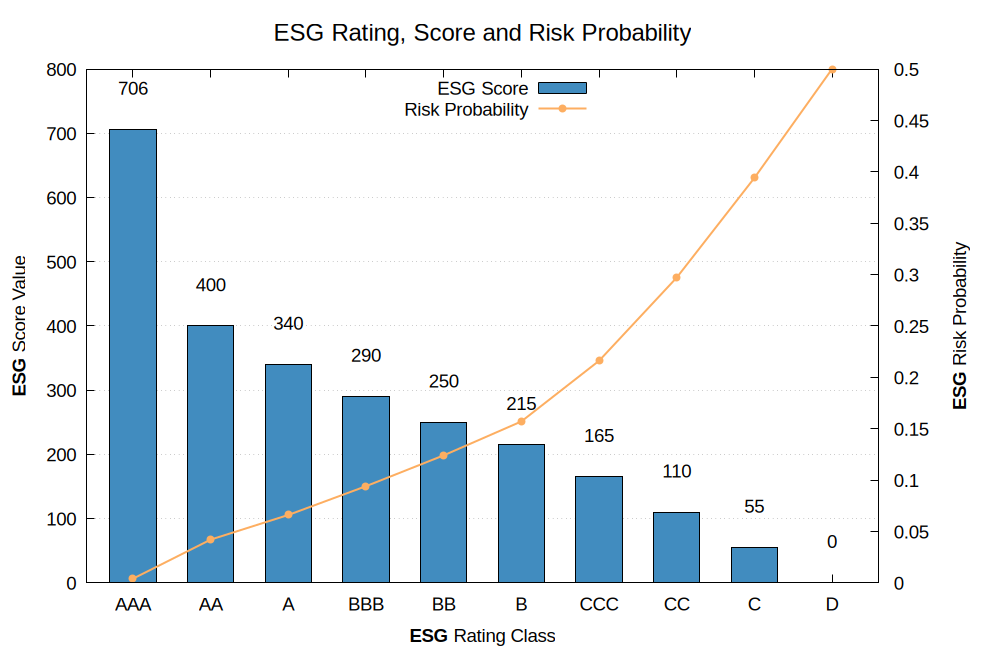
The attached figure shows the Rating scale, defined for each score range and the associated sigmoidal probability function that (increasing as the score decreases) provides a probabilistic interpretation of the set function defined via the score value.

In the following picture, is provided a representation of the ESG score risk probability as a point in the 3 dimensional E, S, G space, where distance between P on different times (and between different companies) is definable and measurable.  

Article Poster as concise summary.

The summary poster had been done also in German and in Italian language as per completeness in order to be as sharable as possible. both are here attached.