Experimental realization of fractal photonic anomalous Floquet topological insulators
Published in Physics

Anomalous Floquet topological insulator (AFTI) is a periodically driven topological insulator (TI), which has nonzero winding numbers to support topological edge modes, though its standard topological invariants like Chern numbers are zero. The photonic lattice constructed by optical waveguide array fabricated by the femtosecond laser direct writing (FLDW) is an important platform for quantum simulation to realize photonic AFTIs. For photonic AFTIs, selective coupling of adjacent waveguides in a cycle is explicitly defined by the discrete periodically driving protocol. At the complete transfer discrete driving protocol, the lattice energy transfer efficiency of the chiral edge mode is the highest among all TIs (close to 100%), so it is very suitable for the transport of fragile quantum states. However, most of photonic AFTIs usually support only one kind of chiral edge mode even at a large lattice size, exhibiting just one chirality and only propagating along the outer boundaries of lattices, which can’t meet the requirement of the scalability for the multi-state topological quantum system and the large-scale optical quantum computation. How to increase the type and number of chiral edge modes in a single photonic lattice is a challenge.
Recently, the emerging fractal TIs generated by selectively removing lattice sites from the normal TIs have attracted much attention for their self-similarity and non-integer dimension. Here, we introduce the fractal into photonic AFTIs to increase the type and number of chiral edge mode in a single lattice, and have demonstrated the first experimental realization of fractal photonic AFTIs in glass using the FLDW technique. The lattice sites are arranged according to the second-generation (G(2)) dual Sierpinski carpet (DSC) structure (Fig. 1a), whose Hausdorff dimension is 1.89D. The coupling between adjacent waveguides is configured according to the complete transfer discrete driving protocol: in each step, only one kind of coupling is switched on when two waveguides approach close to form a horizontal or vertical directional coupler (DC) and the other three are off, and the theoretical transmittivity of each DC is set as 100%. The individual couplings are guaranteed by the specially designed 3D waveguide structure based on DCs, quite different from the previous fractal lattices constructed by identical straight waveguides or helical waveguides. In the fabricated one-period fractal AFTI samples, the number of DCs is up to 88 (Fig. 1a), less than that in a complete lattice, but the coupling behaviors become complex due to the breaking of symmetry and periodicity. By optimally selecting the pulse energy of 470 nJ and the scanning speed of 20 mm/s, all the fabricated waveguides work in single mode with similar performances. Although the cross sections of waveguides fabricated in different depths indeed have slight variations, as shown in Fig. 1b, they don’t dramatically influence experimental results.
Figure 1 | Fractal photonic anomalous Floquet topological insulators. a, A schematic sketch of the fabricated sample with 64 lattice sites (G(2)) in one period z0. b, Micrograph of the facet of the fractal photonic lattice fabricated by FLDW.
It can be found in the quasienergy spectrum of the DSC lattice at G(2), the fractal lattice retains the chiral outer edge mode in the original normal lattice and generates two chiral inner edge modes IEA and IEB, which have the opposite chirality with the outer edge mode and propagate along the inner boundaries of the lattice. The fractal AFTI with fewer waveguides supports 4 kinds of modes: 17 outer edge modes, 7 inner edge modes IEA, 24 inner edge modes IEB and 16 bulk modes. Thus, the number of chiral edge modes carried by a single lattice increases greatly to 48 (Fig. 2).
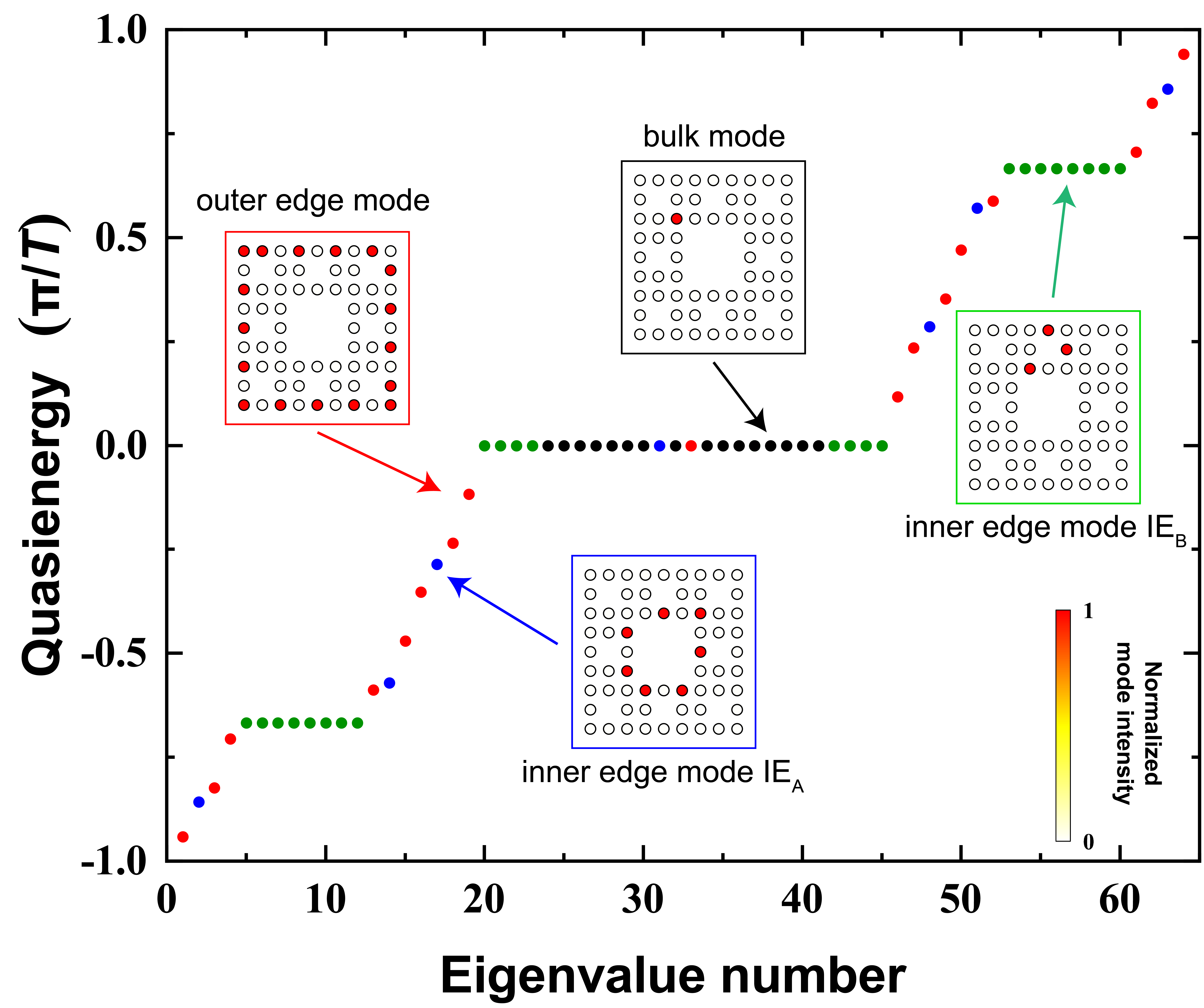
Figure 2 | Quasienergy spectrum of the fractal photonic AFTIs. The black dots represent the bulk modes, and the red, blue, and green dots represent outer edge modes, inner edge modes IEA and IEB, respectively.
By single-site excitation of laser, though there exist coupling strength deviations in the fabricated sample, the measured mode transfer behaviors of chiral edge modes agree well with the theoretical simulation results, indicating the robustness of the chiral edge mode. Furthermore, when the excited light is a pair of correlated photons, the generated single-photon chiral outer edge state and inner edge state are topologically protected in modes distribution and quantum correlation during the quantum state transport in the lattice. The observed high-visibility and well-matched quantum interferences (Fig. 3) verify that multiple propagating single-photon chiral edge states are highly indistinguishable, which provide the potential for generating topologically protected entanglement resources and performing quantum logic operations. What’s more, it is the first experimental work to apply propagating chiral edge modes to quantum state transport in laser-direct-written photonic TIs, instead of zero-dimensional bound modes in all previous works, exhibiting no topological edge transport properties.
Figure 3 | Quantum interference of multiple single-photon chiral edge states in fractal photonic lattice. (a, b, c) Single-photon chiral outer edge state and inner edge state (IEB, IEA, IEA) are transferred from input sites (pink dots) to output sites (yellow dots) in the (one, one, two)-period lattices. The red, blue, and green arrows represent the unidirectional topological transport of single-photon outer edge, inner edge IEA, and inner edge IEB states, respectively. The corresponding quantum interference curves and visibilities V are shown in (d, e, f).
With the growth of fractal generations, the type and number of chiral edge modes in a single lattice increase significantly. When the injected photons are multi-photons, or photons in superposition states or entangled states, the quantum information capacity of a single fractal photonic lattice can be further expanded. Fractal photonic AFTIs can simultaneously carry multiple topologically protected quantum chiral edge states, so they can serve as a stable carrier for high-capacity quantum information transmission. It is expected that they can be used in scalable multi-photon topological quantum computation and quantum simulation of multi-particle systems. In addition to the Sierpinski carpet and Sierpinski gasket, this can extend to many other fractal structures, which can broaden the field of fractal photonic TIs.
Follow the Topic
-
Light: Science & Applications

A peer-reviewed open access journal publishing highest-quality articles across the full spectrum of optics research. LSA promotes frontier research in all areas of optics and photonics, including basic, applied, scientific and engineering results.
Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in