Imagine you are a passionate experimentalist with a love for alloys made of niobium (Nb) and tungsten (W). One day, you decide to embark on a quest to discover the most stable alloys from all possible combinations of these two elements. But here’s the challenge—how can you ensure an exhaustive search without the nagging worry that you might have overlooked an important structure?

The problem lies in the tools available. Popular computational methods for structural discovery—like CALYPSO, PyXtal, and USPEX—tend to focus on identifying individual structures rather than conducting a systematic exploration of all possible alloys.

To tackle this, we asked ourselves: why not simply exhaustively generate and evaluate all possible structures (up to a fixed number of atoms in a supercell, say N = 20), calculate the energy of each configuration, and identify the most stable candidates? The idea sounds foolproof—except for one small hitch. Computing the energy of a single structure using Density Functional Theory (DFT) can take several hours. At that rate, you’d be collecting retirement benefits before you finish exploring structures with even moderately sized supercells ...

Let’s put this into perspective. For a system with 20 atoms in a supercell and just two elements (niobium and tungsten), there are $2^{20}$possible configurations to consider (ignoring symmetry). If calculating the energy of each structure takes 2 hours, the total computational time balloons to approximately $2^{20} \times 2$ hours—that’s over 240 years! Clearly, a more efficient approach is needed.

To calculate the energies of the structures, we proposed using a machine-learning interatomic potential developed by A. Shapeev in 2017, known as the low-rank potential. This powerful tool can compute the energy of a structure in mere fractions of a second. Thanks to its remarkable speed, we were able to bring the idea of exhaustive search to life.

But, of course, the exhaustive search method itself wasn’t as straightforward as it might seem. To further accelerate the process, we considered only non-equivalent structures. The core idea of this method is that for a fixed number of atoms $N$ in a supercell and $M$ atomic species, the number of unique configurations is finite. These configurations arise from distinct atomic arrangements within the lattice nodes (referred to as lattice "colorings") and different supercell shapes. In other words, instead of blindly iterating through all possible structures, our approach efficiently generates and examines only the unique combinations of supercells and colorings. A schematic overview of this algorithm is illustrated in the accompanying video:

All in all, to run the algorithm, you need to specify three parameters:

1. The maximum number of atoms per supercell to be explored.
2. The list of atomic species to consider (e.g., $[Nb, Mo, Ta, W]$).
3. The crystal lattice type shared by all elements in the system (e.g., body-centered cubic (BCC) or face-centered cubic (FCC)).

As part of the alloy discovery process, our algorithm constructs the convex hull—a stability diagram of alloys. This diagram represents the relationship between the formation enthalpy per atom ($\Delta H$, eV/atom) and the composition of the alloy (e.g., the fraction $y/(x+y)$ of tungsten in the binary system $\text{Nb}_x \text{W}_y$). As the number of atoms in the supercell increases, the algorithm considers a growing pool of structures, including increasingly stable candidates, causing the convex hull to deepen, as illustrated in the figure below:

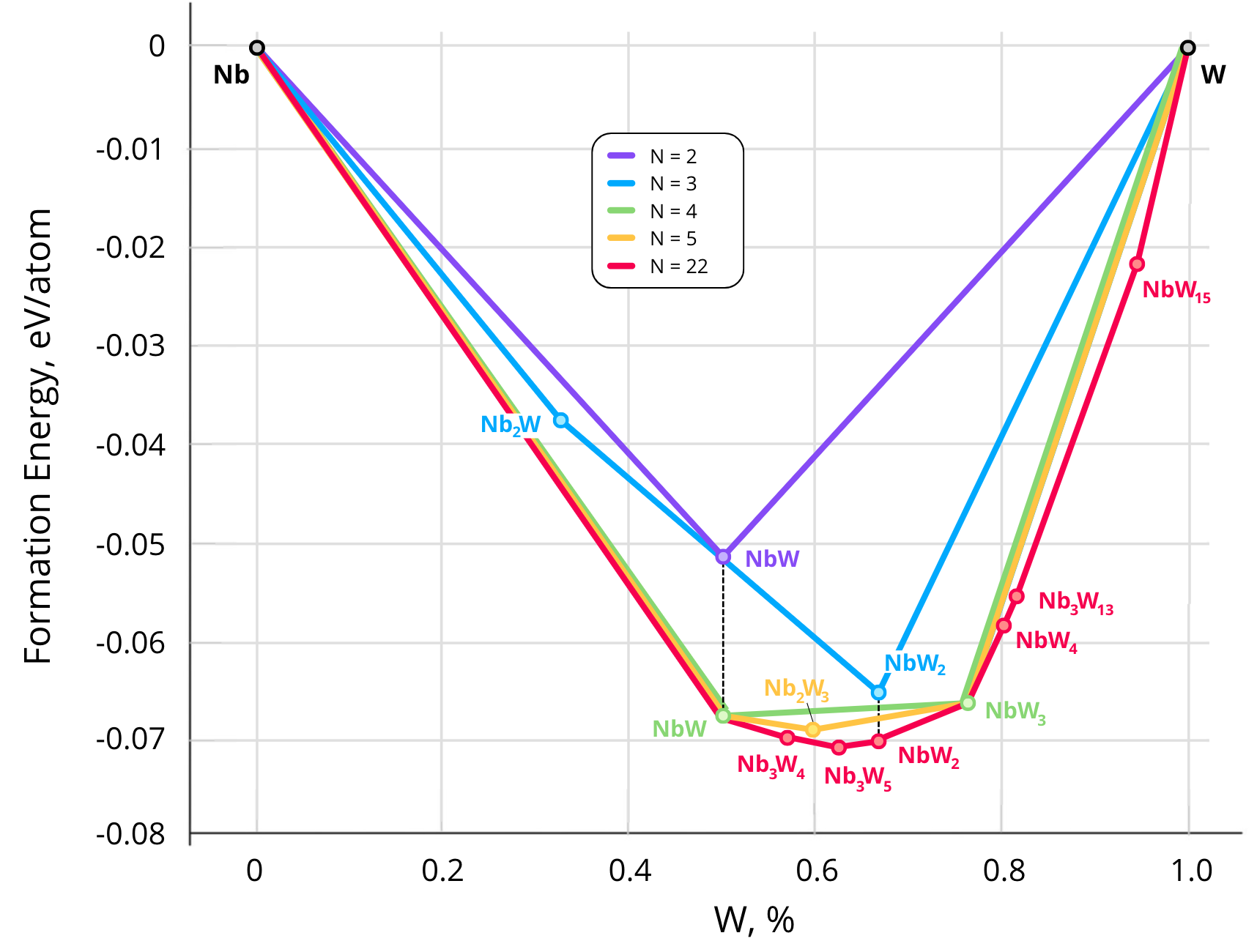
Using this approach, we investigated six systems:

• BCC systems: Nb-W, Nb-Mo-W, and V-Nb-Mo-Ta-W
• FCC systems: Cu-Pt, Cu-Pd-Pt, and Cu-Pd-Ag-Pt-Au

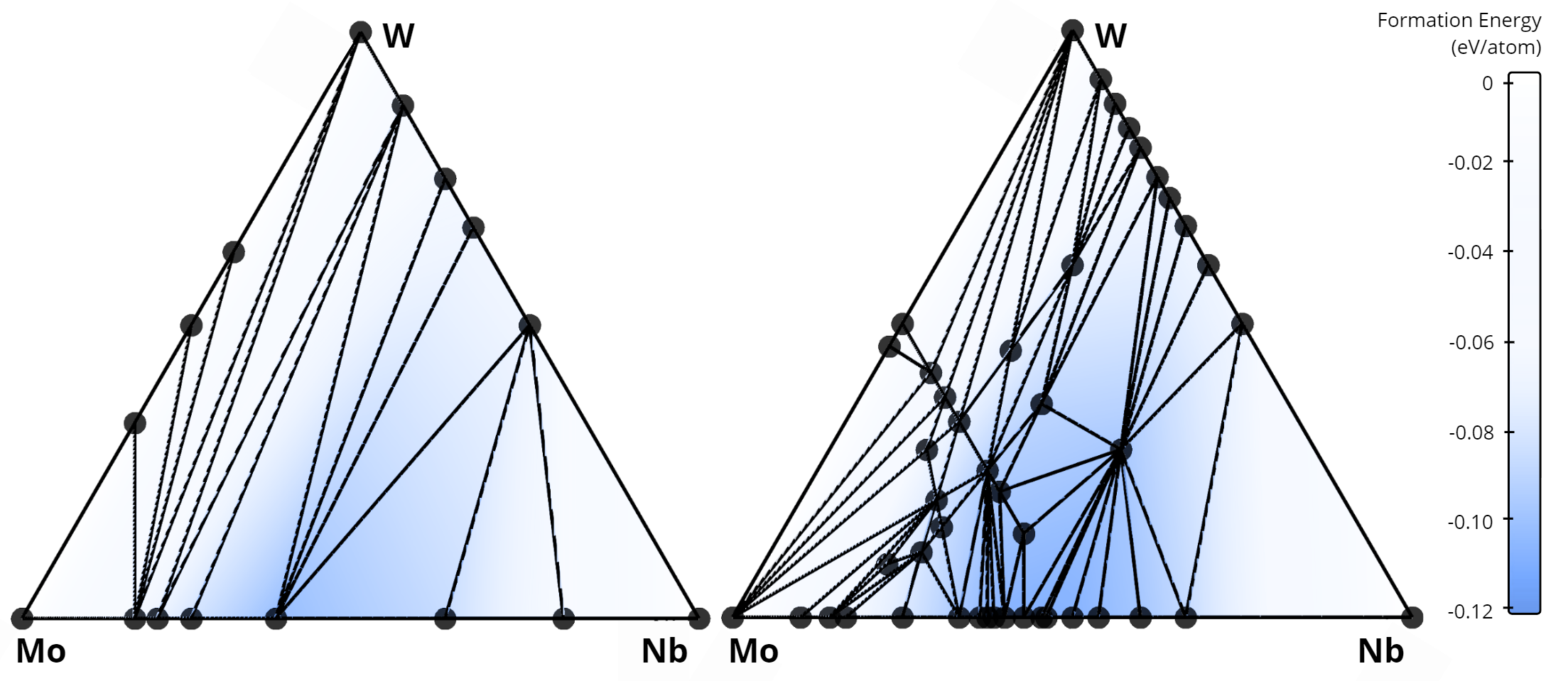
In total, our algorithm identified 268 new alloys that were not previously listed in the AFLOW database. A comparison of the stability diagrams for alloys discovered in this work versus those from the AFLOW database is presented below. For example, in the Nb-Mo-W system, no ternary alloys exist in the AFLOW database (left figure), while our method uncovered 15 new ternary compounds (right figure).

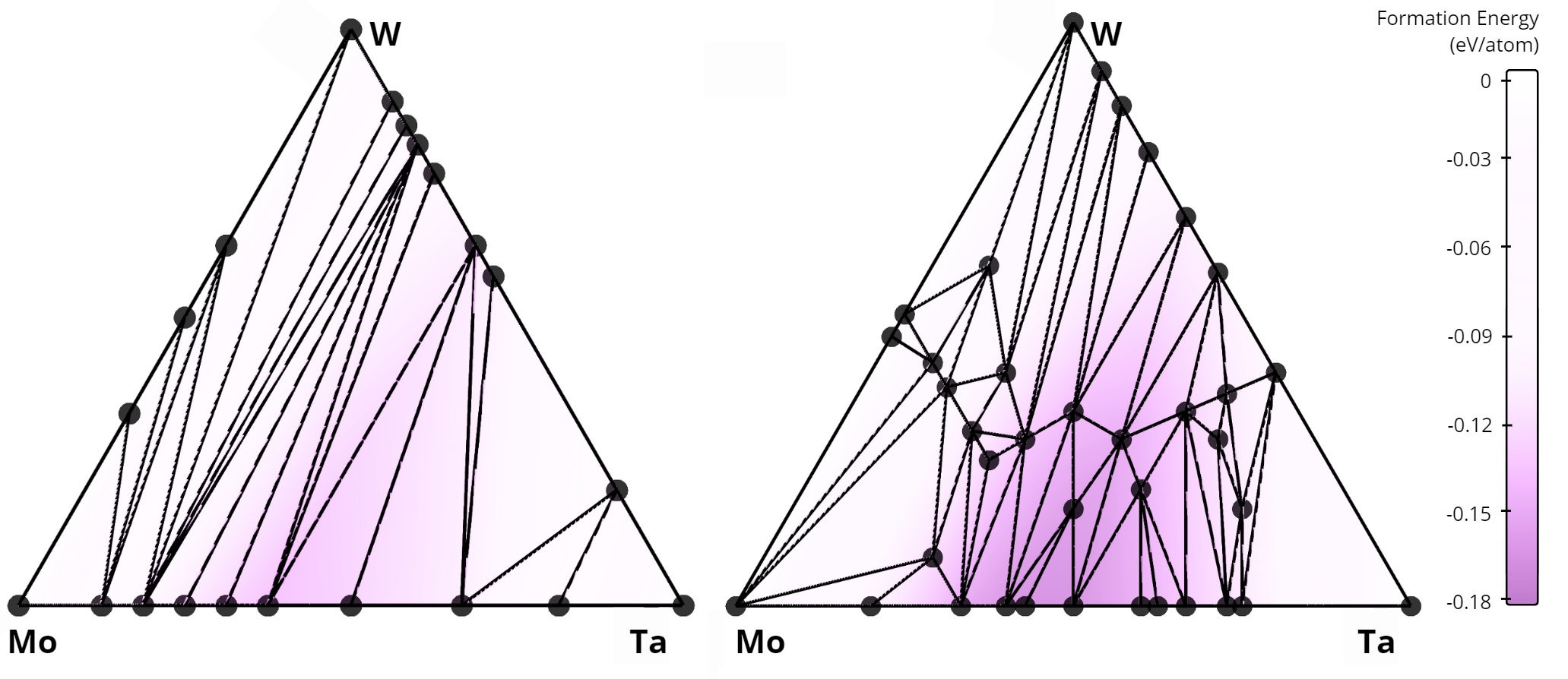
Comparison of convex hulls for the Mo-Ta-W ternary system: 

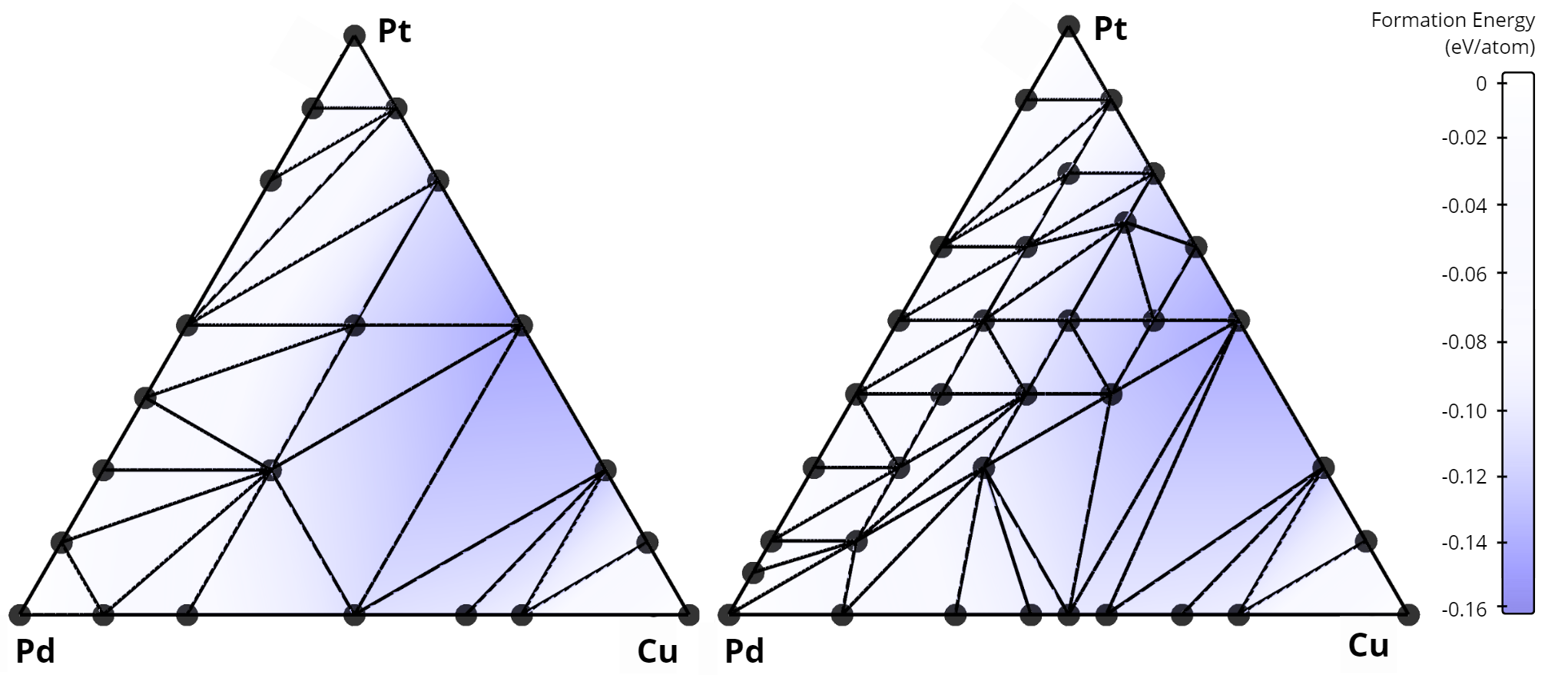
Comparison of convex hulls for the Cu-Pd-Pt ternary system: 

For a more detailed discussion of our results, we invite you to explore our paper! :)