Interaction-driven breakdown of dynamical localization in a kicked quantum gas
Published in Physics

In recent years, quantum mechanics is finding direct application in novel technologies from quantum computers to precision sensors. While these developments make this an exciting time for many experimental physicists, understanding and controlling these technologies remains challenging. A key hurdle is the difficulty of understanding how multiple quantum particles interact. Interparticle interactions are generically present, but can be difficult to control and even to comprehend. This motivates the study of well-controlled systems where quantum behavior is still prevalent in the presence of many-body interactions.
A natural starting point for such study is the quantum kicked rotor (QKR), a paradigmatic system which blends aspects of chaos theory and condensed matter physics. Classically, the kicked rotor consists of a pendulum periodically kicked by gravity, and exhibits a transition from integrable to chaotic dynamics as the kick strength is increased. In the quantum regime, this transition to chaos is marked by a phenomenon known as dynamical localization, a momentum-space analog to the famed Anderson localization. While Anderson localization manifests as a suppression of transport in the presence of randomness, dynamical localization causes suppression of energy growth. While the QKR has been studied extensively in prior cold atom experiments [1,2], the presence of interactions complicates the model considerably. Different theories [3,4] suggest dramatically different behaviors. A fully exact theory of this many-body driven quantum system is well beyond our capabilities, so we must approximate; however, different theoretical approximations give rise to very different predicted behaviors, from anomalous diffusion to many-body localization to other phenomenology. Until now the interacting QKR was experimentally unexplored.
Luckily, one of the experimental platforms in our research group turns out to be ideal for studying the interacting QKR. Our prior work [5] investigated the response of an interacting Bose-Einstein condensate (BEC) when strongly driven by an amplitude-modulated optical lattice. The ingredients of an interacting QKR are similar. The interatomic interaction strength can be controlled with a magnetically-tunable Feshbach resonance, and the QKR hamiltonian can be engineered by kicking rather than sinusoidally modulating an optical lattice applied to the BEC. In addition, the momentum-space distribution can be measured by letting the atoms undergo free expansion, during which states with different momenta move apart in space. These techniques provide all of the necessary tools to study the interacting QKR experimentally, as shown in our Nature Physics publication “Interaction-driven breakdown of dynamical localization in a kicked quantum gas”. During the course of our work, we learned of complementary work being done by Subhadeep Gupta’s group at the University of Washington, which yielded similar results to those discussed below. Their paper, “Many-body dynamical delocalization in a kicked one-dimensional ultracold gas” is published in the same issue. It’s exciting for us that multiple cold atom experiments investigated the interacting QKR simultaneously, as the complementarity of the different approaches really fosters deeper understanding of the complex physics involved.
Results
In the simpler case of the non-interacting QKR, what dynamics do we expect?

In the figure above, a stacked sequence of images reveals the momentum distribution of the atoms as a function of the number of kicks applied. The first few kicks populate non-zero momentum states, but subsequent kicks do not further alter this distribution; in effect, the momentum distribution is "frozen", despite continued violent kicking! This surprising and non-intuitive result showcases the emergence of dynamical localization.
Now let’s add interactions into the mix:

As time progresses and more kicks are applied, the atoms begin to smear between the momentum states due to interparticle scattering, resulting in a blurrier image as you move towards the right in the figure. The way in which these scattering events affect the overall momentum distribution provides insight into how interactions affect dynamical localization. Let’s explore this more quantitatively.
Below is a graph of kinetic energy (proportional to the variance of the momentum distribution) over time for 3 different s-wave scattering lengths (0 a0, 240 a0, and 760 a0 where a0 is the Bohr radius, shown by the circles, squares, and diamonds respectively). Larger values of the scattering length correspond to stronger interatomic interactions.

Here the breakdown of dynamical localization is clear. For the noninteracting sample, the energy stays constant even out to 1000 kicks. As the interactions are increased to 240 a0, there is a departure in energy after a few hundred kicks, and we can see for the 760 a0 case that the energy grows at all times. Crucially, this energy growth is significantly slower than the diffusive growth expected for the classical system, shown by the solid blue line and associated data (triangles) in the inset. This “anomalous diffusion” has been predicted in prior theory work [4], but the good agreement of that prediction with our data is rather surprising due to the 3D nature of the experiment and lack of transverse confinement.
One further method by which we can gain insight is to examine the evolution of the momentum distributions directly. In the figures below, time progresses from yellow to purple, and the two columns show the same data but on different scales (linear vs. log on the y-axis).
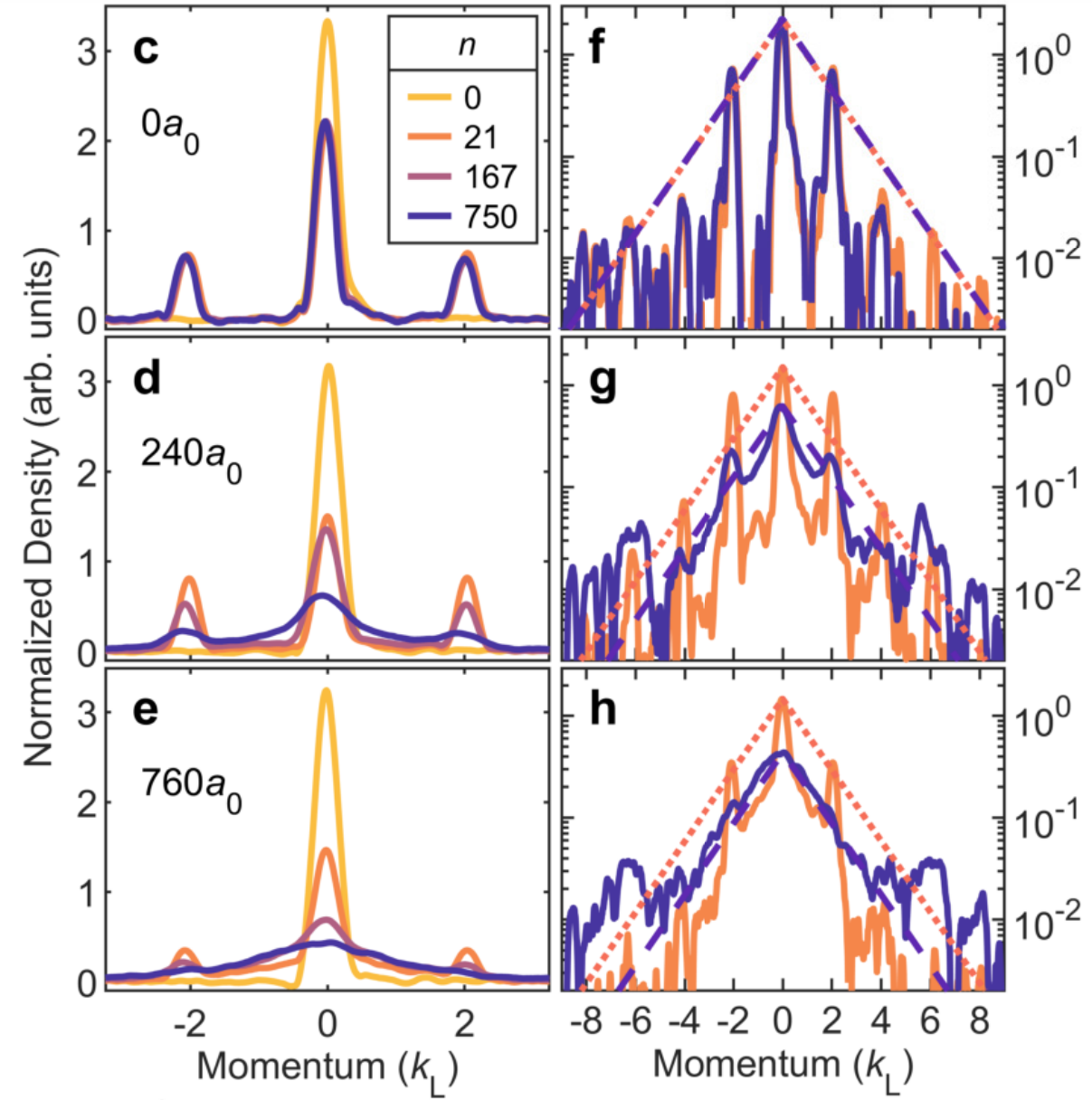 In the noninteracting case (c,f), we can see similar momentum distributions for all values of n past ~10, indicative of the aforementioned “freezing” of the distribution caused by localization. For the larger interaction strengths, we see the smearing expected due to the presence of interactions, but perhaps surprisingly also see a much larger departure in the tails of the distribution (most prominently shown in h, which is plotted logarithmically). This distribution is still not entirely explained, as there is no expectation for the lower energy modes to maintain an exponentially localized envelope.
In the noninteracting case (c,f), we can see similar momentum distributions for all values of n past ~10, indicative of the aforementioned “freezing” of the distribution caused by localization. For the larger interaction strengths, we see the smearing expected due to the presence of interactions, but perhaps surprisingly also see a much larger departure in the tails of the distribution (most prominently shown in h, which is plotted logarithmically). This distribution is still not entirely explained, as there is no expectation for the lower energy modes to maintain an exponentially localized envelope.
This interaction-induced delocalization marks a transition to the regime of many-body quantum chaos, which we can probe in another interesting way. Prior experiments [6] have shown that effective reversal of the flow of time can be achieved by reversing the phase of the kicks in the QKR when on resonance, or equivalently waiting a half period between two equal trains of resonant kicks. This protocol effectively allows us, if nothing interferes with the reversal, to go “backwards” in time after a set number of kicks and return to the initial state. The effectiveness of the procedure can be measured by comparing the final state to the initial state.
An example of this protocol is shown in the figure below.
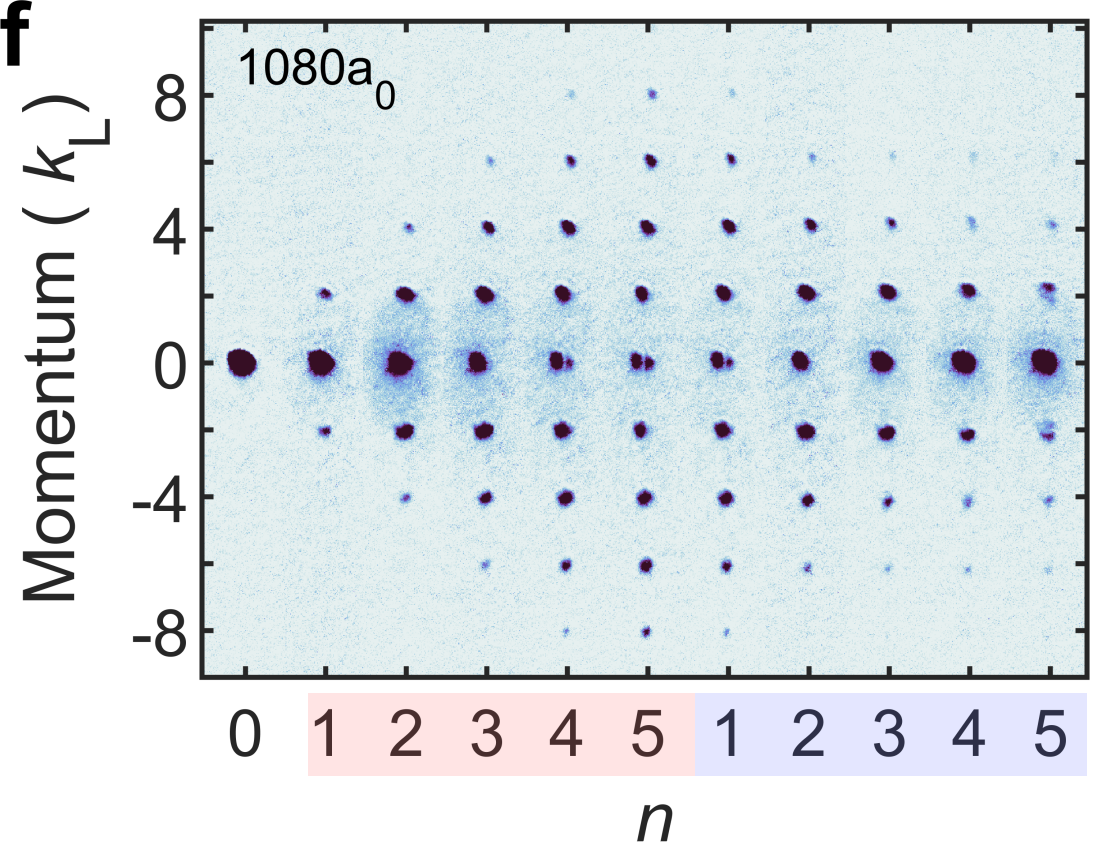 Five resonant kicks are initially applied to the BEC, followed by a half period delay before applying 5 more resonant kicks. We see that once we start applying the second set of kicks, the momentum orders start to “come back” (not to be confused with the famed “quantum boomerang” [7]). If the hamiltonian was perfectly reversed, after the 10th kick we’d observe the initial 0 momentum state again, but the finite momentum width and the inability to reverse the interaction energy modifies this picture. The modification due to the interactions is what we wanted to investigate.
Five resonant kicks are initially applied to the BEC, followed by a half period delay before applying 5 more resonant kicks. We see that once we start applying the second set of kicks, the momentum orders start to “come back” (not to be confused with the famed “quantum boomerang” [7]). If the hamiltonian was perfectly reversed, after the 10th kick we’d observe the initial 0 momentum state again, but the finite momentum width and the inability to reverse the interaction energy modifies this picture. The modification due to the interactions is what we wanted to investigate.
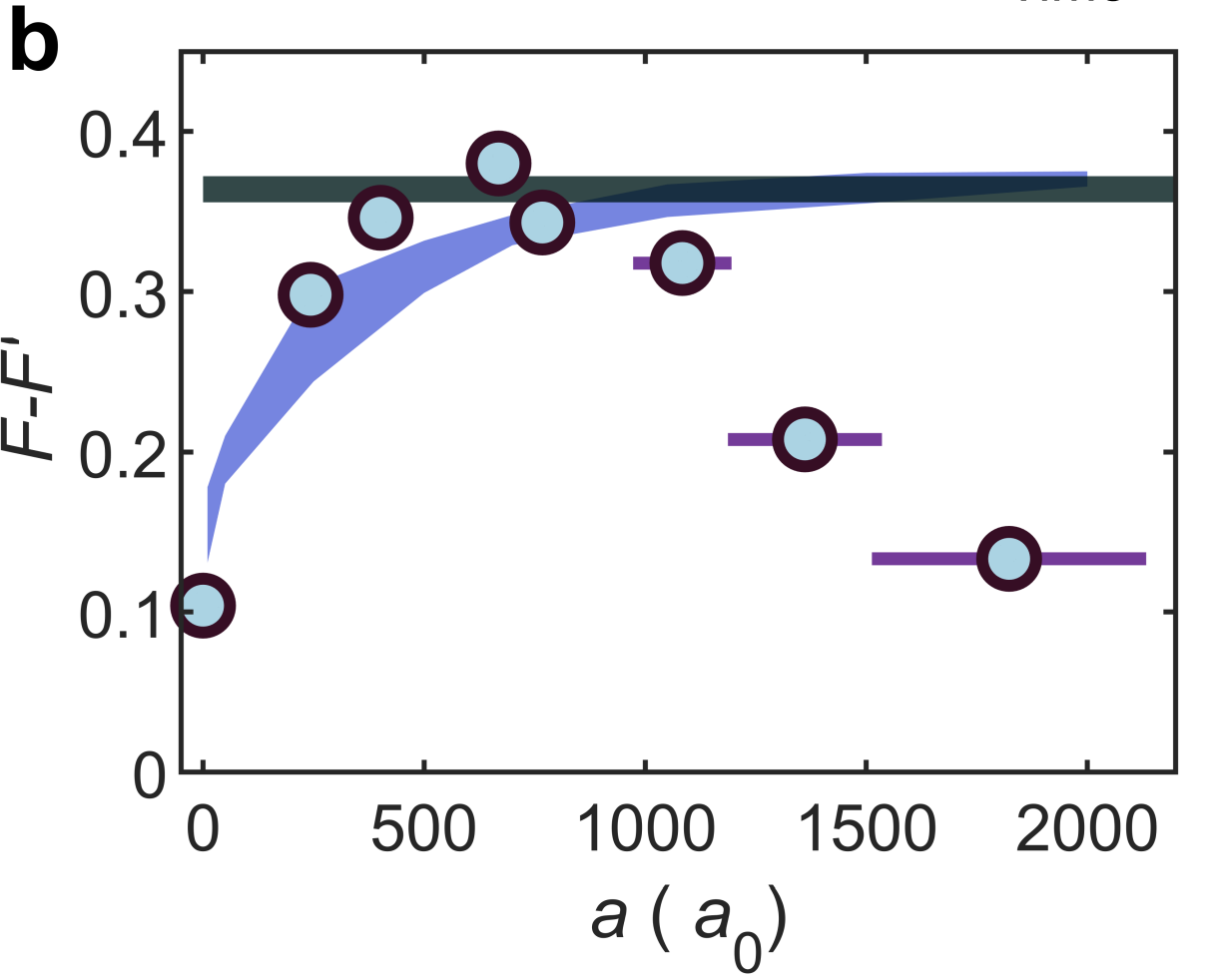 The figure above shows the fidelity, or the degree to which time reversal is preserved, as a function of interaction strength. This brings us to the last surprising point of the experiment: the fidelity is non monotonic with respect to interaction strength! Intuitively, one would expect that as interactions are increased, interatomic collisions would scramble the phase information required to successfully reverse time. While this is true after a certain value, we observe that for smaller interactions the fidelity actually increases as the strength is increased. As unexpected as this seems, the behavior can actually be explained with a fundamental argument about BECs: as the interaction strength is increased, the Thomas-Fermi spatial width increases, and correspondingly the width in momentum space decreases, increasing the fidelity. This is shown by the shaded blue theory curve in the figure. Crucially, this occurs before the collisional time scale of the smaller interaction strengths. As interactions are turned up, interactions dominate the dynamics before the time reversal can occur, inducing irreversibility.
The figure above shows the fidelity, or the degree to which time reversal is preserved, as a function of interaction strength. This brings us to the last surprising point of the experiment: the fidelity is non monotonic with respect to interaction strength! Intuitively, one would expect that as interactions are increased, interatomic collisions would scramble the phase information required to successfully reverse time. While this is true after a certain value, we observe that for smaller interactions the fidelity actually increases as the strength is increased. As unexpected as this seems, the behavior can actually be explained with a fundamental argument about BECs: as the interaction strength is increased, the Thomas-Fermi spatial width increases, and correspondingly the width in momentum space decreases, increasing the fidelity. This is shown by the shaded blue theory curve in the figure. Crucially, this occurs before the collisional time scale of the smaller interaction strengths. As interactions are turned up, interactions dominate the dynamics before the time reversal can occur, inducing irreversibility.
In conclusion, the work discussed here makes new experimental inroads into the larger problem of many-body quantum physics, specifically the intersection of interactions, localization, and quantum chaos. We expect that this work and the ones that follow it will further illuminate ways to preserve quantum information against decoherence, and improve our understanding of many-body quantum systems as a whole.
References:
[1]. F. L. Moore, J. C. Robinson, C. F. Bharucha, B. Sundaram, and M. G. Raizen, Phys. Rev. Lett.
75, 4598 (1995).
[2] J. Chabé, G. Lemarié, B. Grémaud, D. Delande, P. Szriftgiser, and J. C. Garreau, Phys. Rev. Lett. 101, 255702 (2008).
[3] C. Rylands, E. B. Rozenbaum, V. Galitski, and R. Konik, Phys. Rev. Lett. 124, 155302 (2020).
[4] S. Lellouch, A. Rançon, S. De Bièvre, D. Delande, and J. C. Garreau, Phys. Rev. A 101, 043624 (2020).
[5] K. Singh, C. J. Fujiwara, Z. A. Geiger, E. Q. Simmons, M. Lipatov, A. Cao, P. Dotti, S. V. Rajagopal, R. Senaratne, T. Shimasaki, M. Heyl, A. Eckardt, and D. M. Weld, Phys. Rev. X 9, 041021 (2019).
[6] A. Ullah and M. D. Hoogerland, Phys. Rev. E 83, 046218 (2011).
[7] R. Sajjad, J. L. Tanlimco, H. Mas, A. Cao, E. Nolasco-Martinez, E. Q. Simmons, F. L. N. Santos, P. Vignolo, T. Macrì, and D. M. Weld, Phys. Rev. X 12, 011035 (2022).
Follow the Topic
-
Nature Physics

This journal publishes papers of the highest quality and significance in all areas of physics, pure and applied.

Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in