Magnonic Klein and acausal tunneling enabled by breaking the anti-parity-time symmetry in antiferromagnets
Published in Physics

Klein tunneling was first pointed out by Swedish theoretical physicist, Oskar Klein as a paradox. He calculated the reflection and transmission coefficients for an energetic electron incident on a step potential and found from the Dirac equation that the electron transmits to a high step potential without exponential decay [1]. This phenomenon was interpreted by the quantum field theory as a particle-antiparticle pair production across the potential barrier. However, a direct experimental observation of Klein tunneling is difficult due to the large rest mass and high potential energy of fermions. Here, Yuan et al. show that for non-Hermitian antiferromagnets (AFM), chiral magnons serve as a bosonic platform to demonstrate Klein paradox and chiral tunneling in meV regime [2]. In a Feynman’s picture for antiparticles, the tunneling time of an incident AFM magnon-wave packet across a supercritical barrier is negative. The study illustrates the usefulness of chiral magnons to emulate settings of conceptual relevance and their potential for chirality-based magnonic computing.
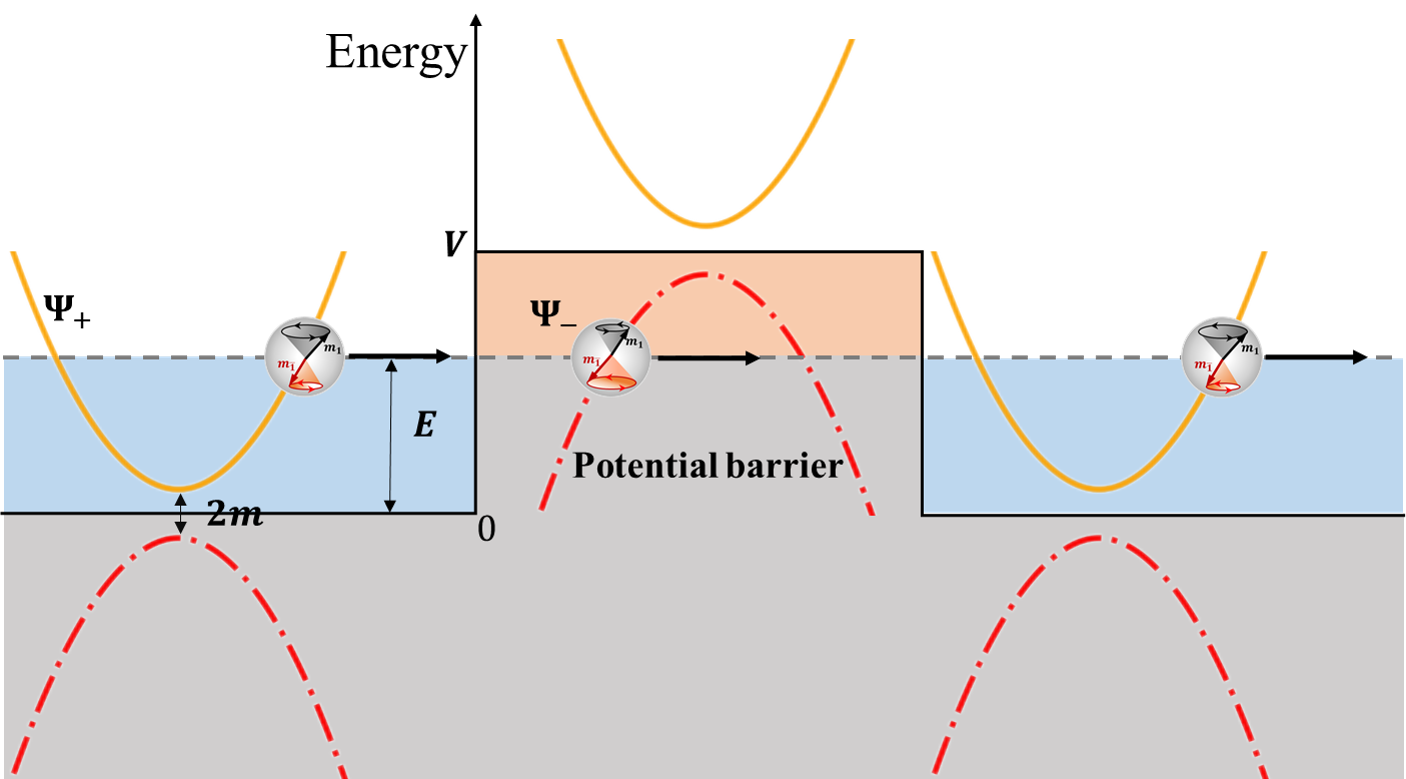
Figure 1: Klein tunneling through a supercritical potential barrier. Ψ± are the right-handed and left-handed magnons in antiferromagnets and can be viewed as particle and antiparticle, respectively. The yellow and red curves are the parabolic energy spectrum of chiral magnons in synthetic antiferromagnets. E is the incident energy located at the region m < E <V-m.
Different from the ferromagnetic (FM) systems that have right-handed magnon chirality, magnons in AFM have both right-handed and left-handed chirality. For realistic materials, the spin wave Hamiltonian of AFMs is anti-parity-time (anti-PT) symmetric and non-Hermitian. In the anti-PT symmetry-preserved phase, spin excitations in the two sublattices are equator modes with a maximally coherent superposition. In the anti-PT symmetry-broken phase, two types of magnons with opposite chirality Ψ± exist in the different sublattices and can be distinguished by the opposite spin precession. While Ψ+ represent the right-handed magnons with a positive energy, Ψ- is associated with the left-handed magnons which have a negative energy. The chirality of magnons develops a positive or negative dispersion, and thus the chiral magnon can be viewed as a particle or antiparticle. Hence, the AFM magnons are suitable objects to test relativistic effects.
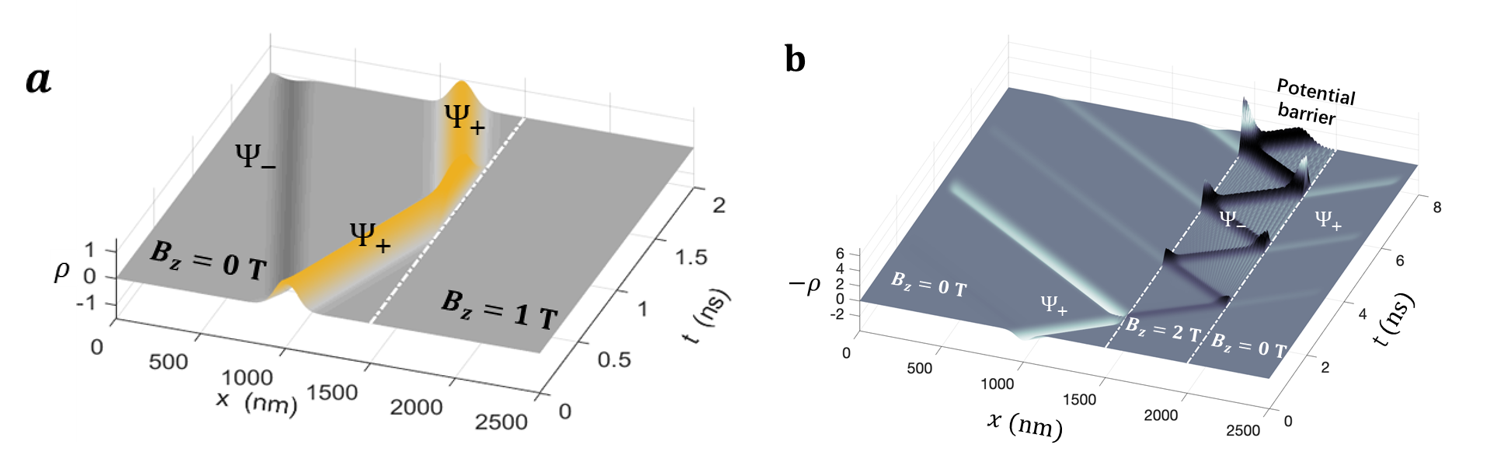
Figure 2: Time evolution of Ψ+ magnon incident into defferent potential barrier. (a) A totally reflection occors when V - m < E < V + m and (b) Klein tunelling apears when the potential barrier increase, satisfying m < E < V - m. Abundance of pairs are produced upon reflection at the barrier’s edges.
An external magnetic field parallel to the easy z-axis act as a potential barrier for the Ψ± magnons. An incident Ψ+ magnon with specific frequency will be completely reflected by a low barrier, as shown in Figure 2(a). However, as the applied magnetic field is increased, an effective energy overlap between the Ψ+ (particle) and Ψ- (antiparticle) state develops at the edge of the potential step. More than 100% of the Ψ+ magnons are reflected back and, at the same time, the Ψ- magnons are spontaneously produced in the interior of the barrier (Figure 2b) which resembles the results of quantum field theory showing that particle-antiparticle pairs can be spontaneously produced in the presence of strong fields. Adopting Feynman’s picture for antiparticles, the Ψ± pair production at the edge of the barrier hints on a negative tunneling time of incoming magnon wave packet across a supercritical barrier.
A strong magnetic field may destabilize the initial Neel ground state resulting in a spin-flop transition in AFM structures. Numerical simulations under initial Neel order indicate that the spin-flop time depends inversely on the Gilbert damping. For a weak Gilbert damping, the spin-flop time can span several tens of nanoseconds at low temperature. Such a time window is large enough to investigate the magnon scattering off the potential step generated by a local magnetic field.
References
[1] Dombey, N. & Calogeracos, A. Seventy years of the Klein paradox. Phys. Reports 315, 41-58 (1999).
[2] Yuan, S., Sui, C., Fan, Z. et al. Magnonic Klein and acausal tunneling enabled by breaking the anti parity-time symmetry in antiferromagnets. Commun Phys 6, 95 (2023).
Follow the Topic
-
Communications Physics

An open access journal from Nature Portfolio publishing high-quality research, reviews and commentary in all areas of the physical sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Higher-order interaction networks 2024
Publishing Model: Open Access
Deadline: Feb 28, 2026
Physics-Informed Machine Learning
Publishing Model: Hybrid
Deadline: May 31, 2026


Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in