Non-Kramer's Doublets and Nematicity
Published in Physics

One hundred years ago, Otto Stern and Walter Gerlach measured the deflection of a beam of silver atoms in a magnetic field gradient and discovered that electrons carry intrinsic magnetic moments. The size of these moments is usually characterized by the g-factor, which counts the multiples of Bohr magnetons. Free electrons have g=2 (albeit with corrections on the order of 0.1 percent due to quantum electrodynamics).
When electrons are bound in atoms and solids, the g-factor can change due to the orbital motion of the electron around a nucleus. In some lanthanide ions, the g-factor can exceed 10. Such large numbers are directly responsible for recent technological advances utilizing miniaturized rare earth magnets, such as those used for wireless earbuds.
In some solids the combination of the spin-orbit and crystalline electric field interactions split the energy levels of the different spin states and alters the g-factor. Kramer's theorem ensures that for half-integer spins, at least one pair of states remains degenerate in the absence of magnetic fields. These pairs of states can be described as an effective spin-1/2 with a re-normalized g-factor. For so-called non-Kramer's ions, the g-factor of the ground state doublet vanishes entirely.
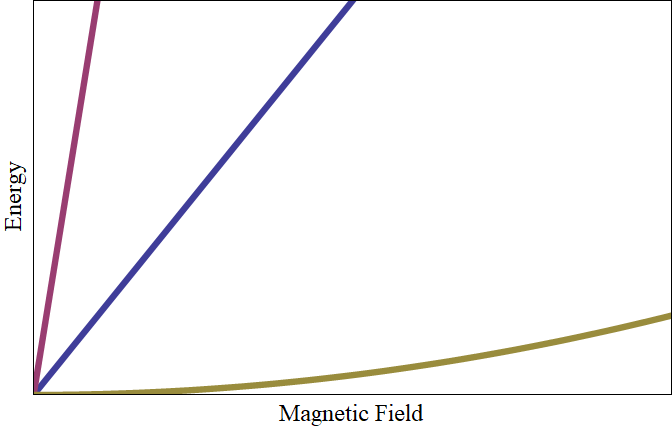
with a nonlinear Zeeman interaction, respectively.
When the g-factor is zero, it opens the door to exotic new physics. As any student of quantum mechanics knows, the Zeeman interaction in a magnetic field lifts the degeneracy of a doublet with an energy difference that is linearly proportional to the g-factor, illustrated at right. For a non-Kramers ion, the energy difference grows only quadratically with field. One consequence may be that long-range magnetic order may be absent - after all there are no magnetic moments in zero field- so other interactions become important. If the electronic orbitals are not spherical (as is often the case), then the quadrupolar moment of the orbital can distort (strain) the lattice. This effect leads to an effective coupling between quadrupolar moments, which can then undergo long-range ferroquadrupolar order.
TmVO4 is the poster child for ferroquadrupolar ordering of the non-Kramer's Tm ions, and although it was studied several decades ago, it is currently enjoying a resurgence of interest as a model system for studying electronic nematicity. Nematicity refers to the spontaneous lowering of discrete rotational symmetry driven by the electronic degrees of freedom, such as in a ferroquadrupolar ordered system. Many strongly correlated electron systems, such as the iron-based and cuprate superconductors exhibit nematicity, and theoretical models suggest that quantum critical nematic fluctuations may drive unconventional superconductivity. TmVO4 is insulating and has no superconductivity, but it does exhibit nematic order that can be continuously suppressed to zero at a quantum critical point that is elegantly described by the transverse field Ising model. Here the transverse field is either a magnetic field along the c-axis, or a strain field with a symmetry orthogonal to the spontaneous strain in the ordered state. An open question is how the system should respond to a magnetic field perpendicular to the c-axis, where the g-factor vanishes.
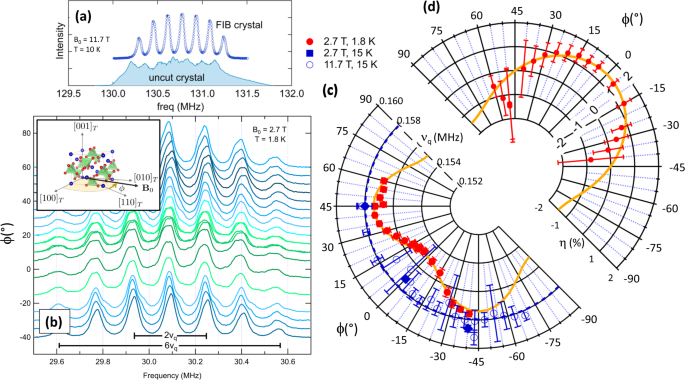
To better understand this system, we studied the nuclear magnetic resonance (NMR) of the 51V nucleus, which couples to the electric field gradient, and is a sensitive measure of the distortions the crystal undergoes when it orders. These experiments require the use of a strong magnetic field. When an arbitrarily shaped crystal is placed in a magnetic field, the field lines near the boundaries of the crystal are distorted, causing an inhomogeneous distribution of NMR resonance frequencies that wreaks havoc with analysis of experimental data. To overcome this problem, we used a plasma focused ion beam (FIB) to cut our crystal into a perfect ellipsoid. This shape ensures a uniform magnetic field within the sample, giving us beautifully sharp NMR resonances and enabling us to carefully track the anisotropy of the EFG, illustrated in the figure below.
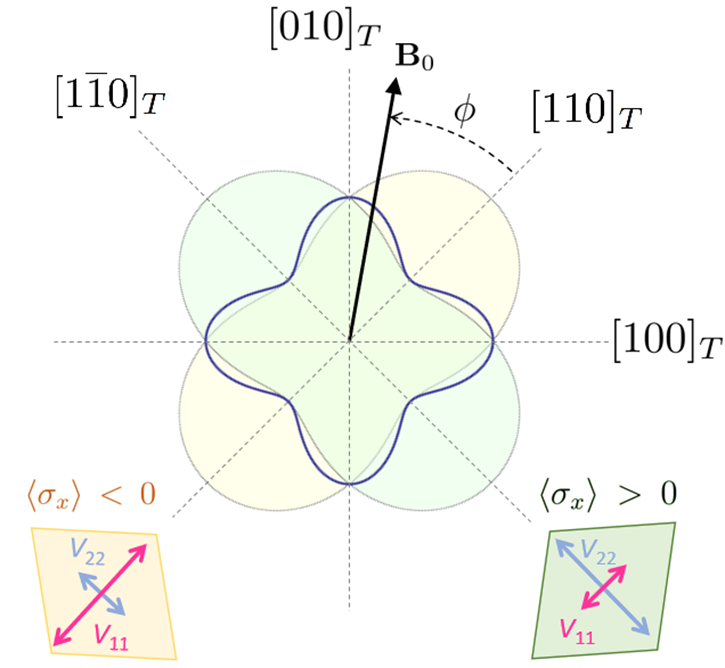
direction. The green (yellow) regions illustrate the quadrupolar splitting
of the two domains. The Zeeman interaction couples the magnetic field to
the lattice strain and detwins the crystal, leading to the four-fold behavior
shown by the blue line.
Surprisingly we found that the anisotropy exhibits four-fold, rather than two-fold symmetry. The reason for unusual symmetry is that the magnetic field couples to the strain and detwins the ferroquadrupolar domains. The coupling has the form εxy*Hx*Hy, where εxy is the lattice strain (or the order parameter). Even though there is no in-plane magnetic moment for the non-Kramer's ion, a moment can be induced by the magnetic field by mixing in excited states. The induced moment can then interact with the field to second order. This effect is analogous to the Stark effect in an atomic s-orbital that is taught to undergraduate students learning about second-order perturbation theory. The difference is that in this case, the Hilbert space is finite so the induced moment can be calculated completely. Interestingly, a field along the x-direction can induce a moment along the y-direction, because the distortion changes the principal axes so that they are no longer along x and y.
Another important consequence of the second order Zeeman interaction is that a field perpendicular to both the c-axis and the ferroquadrupolar distortion direction (along [110]) can also continuously suppress the nematic order to a quantum critical point. The critical field along the c-axis is only 0.5 T, but the in-plane critical field is around 9 T. This means that there is a line of quantum critical points for fields within the a-c (or b-c) plane. Importantly, if there is any field component parallel to the nematic direction, then the sharp ferroquadrupolar transition disappears and becomes a broad crossover.
The non-linear Zeeman interaction of non-Kramer's ions thus provides a new dimension to the physics first uncovered 100 years ago by Stern and Gerlach, and is helping to shed light on the modern topic of quantum criticality.
Follow the Topic
-
npj Quantum Materials

An open access journal that publishes works that significantly advance the understanding of quantum materials, including their fundamental properties, fabrication and applications.
Related Collections
With Collections, you can get published faster and increase your visibility.
Intertwined Orders in Quantum Materials – In Memory of Daniel Khomskii
Publishing Model: Open Access
Deadline: May 13, 2026
Altermagnetic Materials and Phenomena
Publishing Model: Open Access
Deadline: Apr 30, 2026



Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in