Semiclassical relativistic stars
Published in Physics
Explore the Research

Semiclassical relativistic stars - Scientific Reports
Scientific Reports - Semiclassical relativistic stars
Neutron stars represent the most compact relativistic stars known to exist. By compactness, we refer to the amount of mass that is contained within their total radius. From dense and rapidly spinning pulsars to dim and dillute main sequence stars, the same principle applies: hydrostatic equilibrium. Physical systems subject to this phenomenon exist thanks to a clash between the repelling forces caused by usual matter and the attractive tendency generated by their own gravitational pull. In the relativistic regime, that is, when the pressure exherted by the fluid that conforms the star is comparable to its rest energy, highly compact stars meet their own end, as these repulsive forces become a source of gravitational attraction themselves. This implies the existence of a theoretical upper compactness limit, the Buchdahl limit, beyond which gravitational collapse cannot possibly be resisted by conventional matter. The present consensus stablishes that any object whose compactness surpasses Buchdahl limit must inevitably be a black hole, that is, a purely gravitational configuration where all matter has collapsed towards a singularity.
Nevertheless, given the existence of an ample compactness gap between the Buchdahl and black hole limits, it is also fair to expect the emergence of new sources of quantum repulsion in situations of extreme compactness. In our recently published article in Scientific Reports, we have provided robust evidence for the existence of new figures of stellar equilibrium that surpass Buchdahl limit. These so-called semiclassical relativistic stars describe a new stage in stellar evolution where the quantum nature of matter fields carries out a prominent role. As there is no upper bound to their compactness, semiclassical relativistic stars have the potential to supplant black holes as the most compact objects existing in our Universe. In that hypothetical scenario, black holes would correspond to extremely simple (they are only described by their mass, charge and spin) yet remarkably accurate mathematical idealizations of more complex physical situations described by stellar objects without singularities nor event horizons.
The key to this novel result resides within quantum field theory in curved spacetimes (QFTCS), a theory that studies the behaviour, in presence of gravity, of the very same fields that give rise to conventional matter in the first place. These quantum matter fields are physical entities that permeate our whole Universe. Being described by an infinite collection of quantized harmonic oscillators, their vacuum state (or state of minimum-energy) has some nonzero energy associated to it. In absence of gravitational sources, when spacetime is flat from the viewpoint of Einstein's general theory of relativity, these vacuum energies can be renormalized to zero. On the contrary, in curved spacetimes like those describing a compact star or a black hole, vacuum energies get modified by the presence of gravity (a phenomenon known as vacuum polarization), consequently exherting a backreaction onto the background spacetime. The theory that describes this feedback mechanism between gravity and the vacuum is known as semiclassical gravity.
Semiclassical gravity is commonly regarded as an approximation to a theory of quantum gravity, since it considers spacetime (the gravitational field) to admit a classical description, while the material sources that give rise to it can be both classical and quantum. The quantity that codifies contributions to spacetime curvature coming from the vacuum polarization of quantum fields is the renormalized stress-energy tensor or RSET, for short. The RSET is suppressed by Planck's constant so, in ordinary situations (in stars like our Sun, for example), vacuum polarization effects can be safely neglected and we recover Einstein's theory of general relativity, where the compactness of hydrostatic equilibrium configurations is bounded from above by the Buchdahl limit. In extreme scenarios of high compactness like those explored in this work, the RSET can provide a significant contribution that must be taken into account.
In general, computing the RSET is technically challenging. In our work, we appealed to a simplifying approximation (known as Polyakov approximation) that estimates the RSET in a four-dimensional spacetime by the less intricate RSET that arises in a fictitious two-dimensional situation. The resulting RSET is unique up to specifying a single function of the distance to the center of the star. We explored broad families of radial functions that returned similar results, finding that the Polyakov RSET grows significantly in the interior of compact stars that approach the Buchdahl limit.
A crucial aspect behind this discovery is that vacuum polarization has the remarkable feature of inducing negative energetic contributions similar to those arising in the Casimir effect. According to Einstein's theory, negative energies produce a gravitational repulsion, so when a star is made to approach the breakdown of hydrostatic equilibrium, strong repulsive effects kick in drastically and backreact on its interior. This quantum-originated repulsion balances the gravitational pull of the star and allows the existence of equilibrium configurations that surpass Buchdahl's compactness limit.

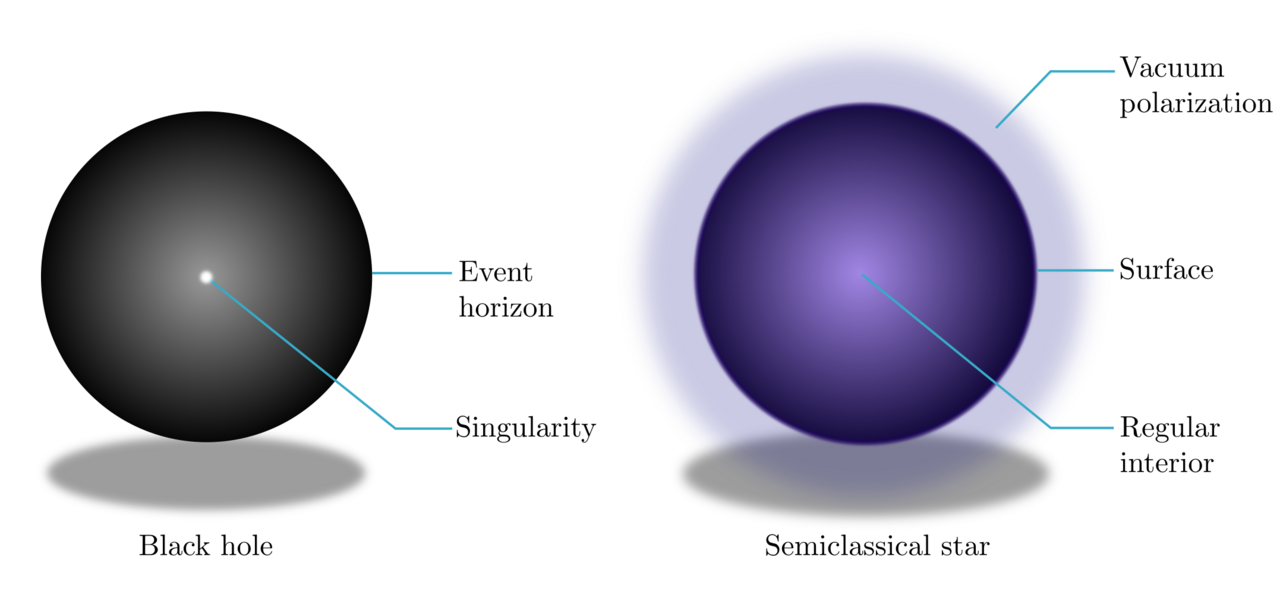
Figure 1. Left: A Schwarzschild black hole is characterized by its mass and exhibits an event horizon covering a singularity.
Right: A semiclassical star is formed by a mixture of classical matter and quantum vacuum polarization. It exhibits a surface and its interior is devoid of singularities.
Are black holes idealized approximations to more complex (stellar) configurations?
The resulting objects conform a new type of star composed by a mixture of a classical matter fluid and a cloud of vacuum polarization. They are characterized by having a negative-mass interior, although the total mass of the star is positive. We have found no further upper bound to the compactness of semiclassical stars, nor any limit to how massive they can be, thus being able to represent both stellar-mass and supermassive black holes. Moreover, the gravitational redshift suffered by the light rays that scape from the interior of these structures is very large, potentially mimicking some of the observational properties of black holes. The new observational capabilities promise an exciting decade in terms of discerning the true nature behind black holes.
Follow the Topic
-
Scientific Reports

An open access journal publishing original research from across all areas of the natural sciences, psychology, medicine and engineering.
Related Collections
With Collections, you can get published faster and increase your visibility.
Obesity
Publishing Model: Hybrid
Deadline: Apr 24, 2026
Reproductive Health
Publishing Model: Hybrid
Deadline: Mar 30, 2026




Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in