Stabilization of a cyclic network of strings by nodal control
Published in Mathematics
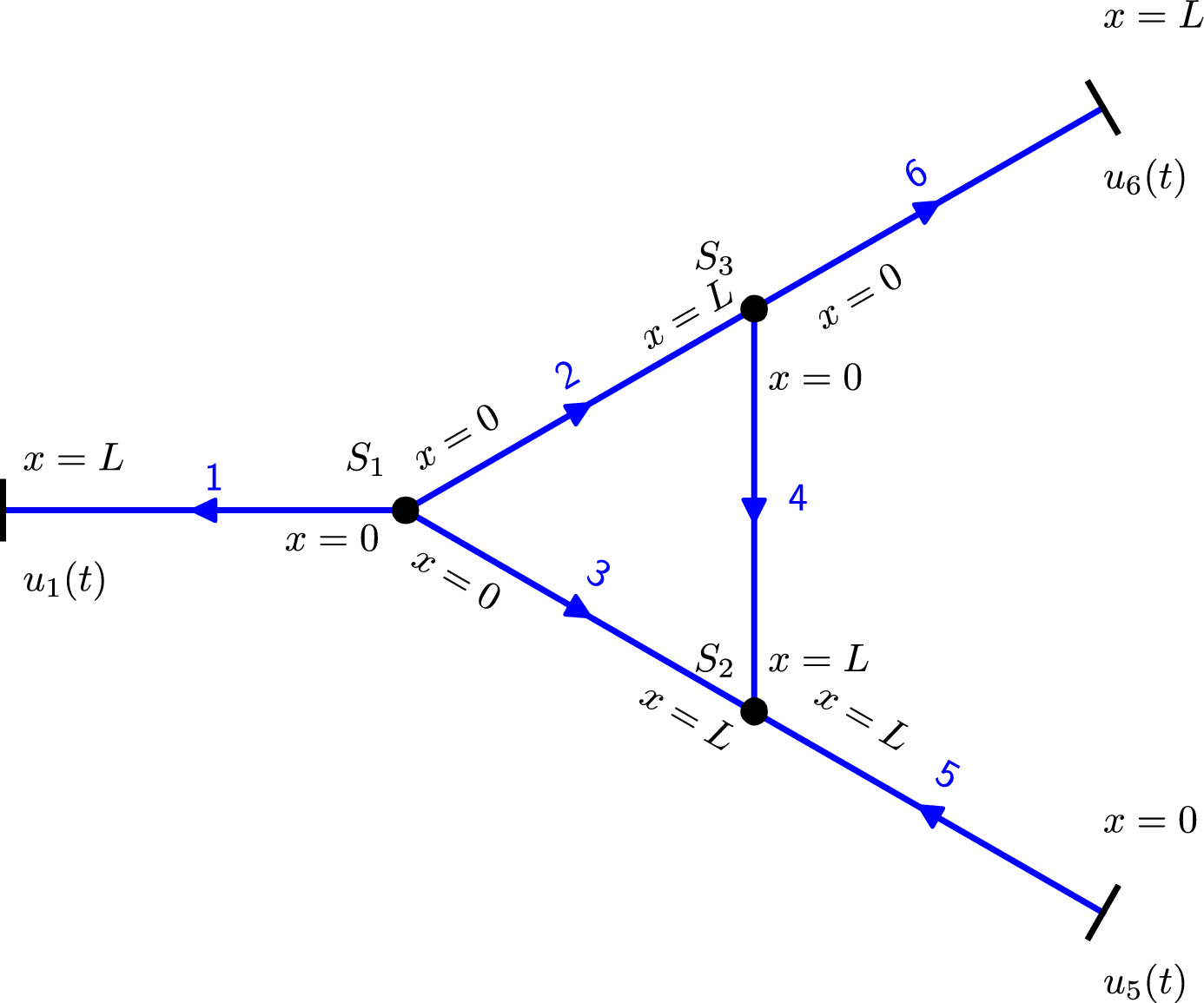
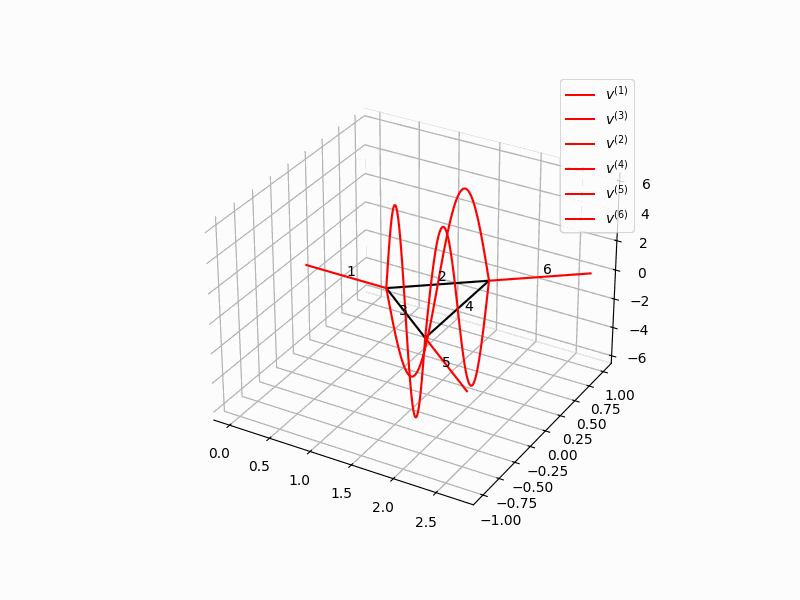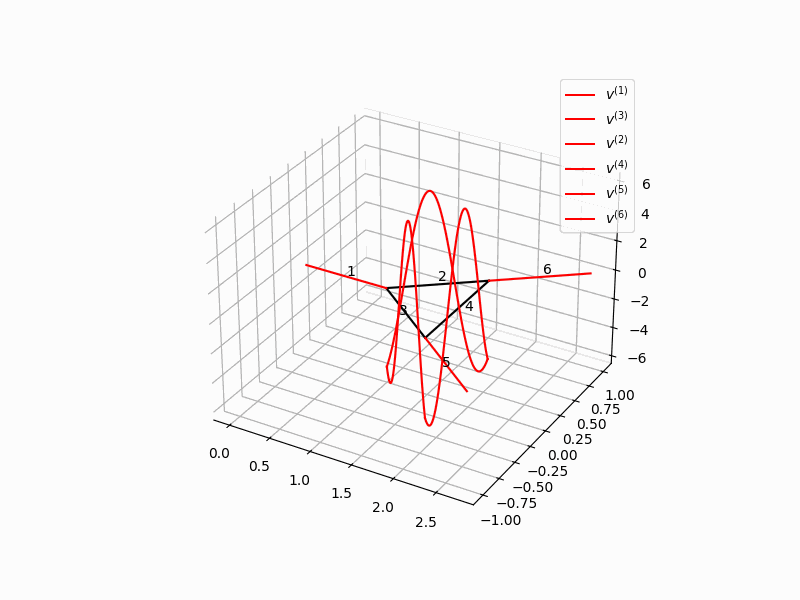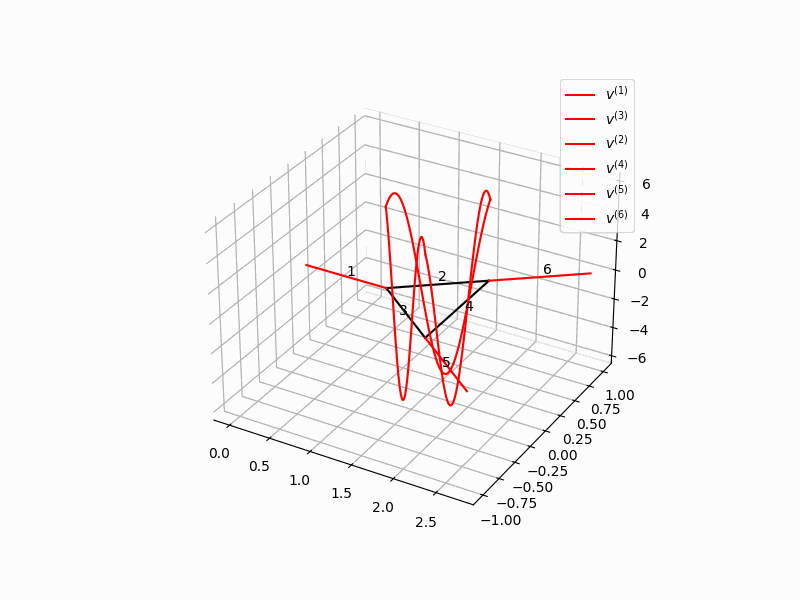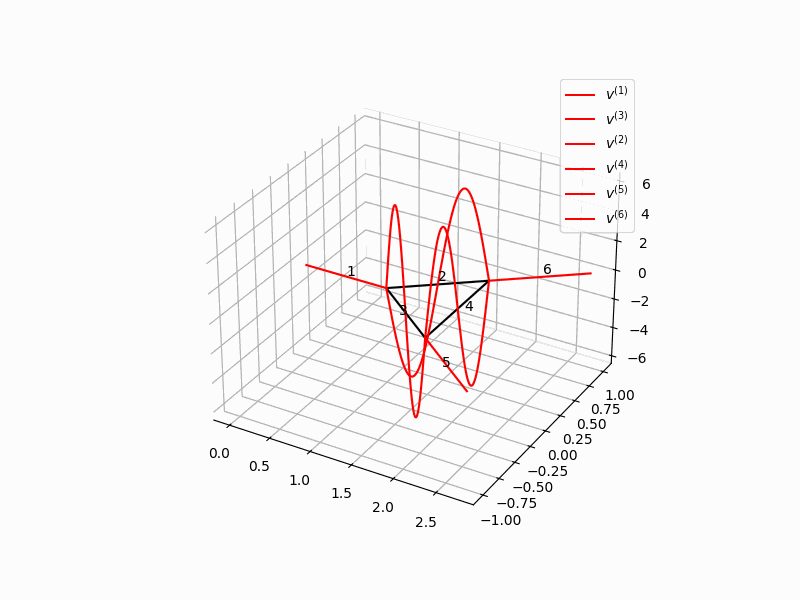In stabilization problems for networked systems, often the situation is much simpler if the graph of the network is given by a tree than in the general case of a graph that can contain cycles. In the literature, often only the case of tree-shaped graph is considered. Since form many applications, typically graphs with intertwined cycles occur, in this paper we have considered a network with a cycle. Since the graph only contains one single cycle, an explicit analysis of the state is possible. We consider a string network an present a traveling waves solution on the graph. It turns out that in order to stabilize the system, it is mandatory that control action also is located within the cycle. Moreover, control of Neumann type does not suffice for stabilization. Only with an additional Dirichlet control exponential stabilization is possible.
Our driving application is the operation of gas networks. The graphs of the pipeline networks regularly contain cycles. This investigation took place within the framework of the Transregio 154 that is funded by the Deutsche Forschungsgeminschaft (DFG). As it is stated on the webpage of the TRR 154, (see https://www.trr154.fau.de/trr-154-en/), its aim is to achieve progress in
Science for energy transition:
'The “turnaround in energy policy” is currently in the main focus of public opinion. It concerns social, political and scientific aspects as the dependence on a reliable, efficient and affordable energy supply becomes increasingly dominant. On the other side, the desire for a clean, environmentally consistent and climate-friendly energy production is stronger than ever.'
One of the interesting topics in this subject area is hydrogen blending to support an increasing role of hydrogen in the energy mix, see also
An Observer for pipeline flow with hydrogen blending in gas networks: exponential synchronization
SIAM Journal on Control and Optimization, Vol.. 62, No. 4, pp. 2273-2296 by
MARTIN GUGAT AND JAN GIESSELMANN (2024)
https://doi.org/10.1137/23M1563840.
In this publication, the gas flow in pipeline networks are studied for general graphs of the networks. Also in this application, the control actuators are located at a finite number of points in the system. This is in contrast to the situation of distributed control where the control action is distributed on the whole networks or more generally on subsets of positive measure,see for example
Observer-based data assimilation for barotropic gas transport using distributed measurements
For the stabilization analysis, both in the case of nodal and distributed control action Lyapunov functions are an extremely valuable tool especially for systems that are governed by quasilinear dynamics. However, in the paper Stabilization of a cyclic network of strings by nodal control a different technique is used, that allows to determine the precise maximal growth rates that can occur in the system. It is bases on the analysis of eigenvalues and thus related to spectral analysis that is present in Gugat, Martin, Xu Huang, and Zhiqiang Wang.
Limits of stabilization of a networked hyperbolic system with a circle.
Control and Cybernetics 52 (2023), see
file:///C:/Users/mpm218/Downloads/Gugat-et-al-2.pdf
As stated in abstract, this paper
'is devoted to the discussion of the exponential stability of a networked hyperbolic system with a circle. The analysis extends an example by Bastin and Coron about the limitsof boundary stabilizability of hyperbolic systems to the case of a networked system that is defined on a graph which contains a cycle. By spectral analysis, we prove that the system is stabilizable while
the length of the arcs is sufficiently small. However, if the length of the arcs is too large, the system is not stabilizable. Our results are robust with respect to small perturbations of the arc lengths. Complementing our analysis, we provide numerical simulations that
illustrate our findings.'
In the TRR 154, the support of young scientists plays an essential role, this is reflected in the contributions in
https://www.linkedin.com/company/crc-transregio-154/posts/?feedView=all.
My research interest are Optimization, Optimal Control, Optimization and Optimal Control under Uncertainty modelled with Chance Constraints and Stabilization.
Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in