Static vector solitons in a topological mechanical lattice
Published in Physics

Concise networks consisting of nodes and bonds have been extensively developed to capture the properties of various systems, from DNA mobility1 to allosteric behaviors of proteins2,3, epithelial morphogenesis4, and jamming in granular materials5. Mechanical networks (lattices) provide a platform to explore the mechanical counterparts of topological insulators, due to the correspondence between classic phonon modes and quantum electronic states. A class of lattices on the verge of mechanical instability, i.e., Maxwell lattices6, have balanced numbers of degrees of freedom and constraints in the bulk and can host zero modes at their free boundaries. Interestingly, infinitesimal zero modes can become finitely deformable and propagate in one-dimensional topological lattices in the form of solitons7. However, nonlinear excitations in topological mechanical systems with multiple zero modes remain elusive.
To extend the concept of solitons in topological lattices described by a scalar field theory, we report vector solitons in a topological mechanical lattice, illustrating the interaction of dual degrees of freedom. Our inspiration for this study derives from the coupled double chains of indium atomic wires with sublattice symmetry breaking8,9. Different from the long-range interactions of atomic chains, our topological lattice is comprised of interconnected bonds and hinged rhombic linkages pivoted to the laboratory frame, showcasing glide-reflection symmetry (Figure 1a). The balanced numbers of length constraints and degrees of freedom in the bulk demonstrate that the mechanical lattice is a Maxwell lattice. Cutting interconnected bonds at two ends unleashes two additional degrees of freedom in the lattice with open boundaries. We are curious about what nonlinear excitations correspond to different zero modes.
To address this, we calculate the two orthogonal zero modes in the absence of self-stress using the Maxwell-Calladine index theorem10(Figure 1 a and b). Then, we conform the lattice along these modes by gradually nudging the node situated at the polarized boundary. On one hand, the transformed configuration along the horizontal direction exhibits a domain wall, displaying a classical kink profile for the horizontal nodal positions, while the vertical components remain zero (Figure 1c). On the other hand, the deformed nodes along the vertical direction demonstrate co-propagating kink and antikink across the lattice (Figure 1d). More interestingly, the topological mechanical lattice shows four transformable homogeneous configurations and domain walls that interpolate different states among them
To unravel the physics underlying these nonlinear responses, we build a continuum model and derive the coupled equations. We find that these equations resonate with realms known for multiferroic phase transitions, nonlinear optics, and multispecies condensates11, supporting vector soliton solutions. The term ’vector solitons’ here describes the nodal positions of zero-energy configurations, triggered with minimal energy input, different from the elastic pulses prevalent in monostable elastic metamaterials with coupled translational-rotational components and amplitude gaps12,13. Furthermore, we find that the vector soliton supports superposed sub-solitons, a unique phenomenon in soliton physics, shedding light on soliton collisions. To observe sub-solitons that approach or depart from each other, we demonstrate the evolution of a domain structure along linearly superposed modes (Figure 1e). This unveils three distinct phases separated by two domain walls (Figure 1f), with the vector soliton’s components emerging as the sum or the difference of two kinks, which reflect the transfer of quantized degrees of freedom from the boundary into the bulk of the lattice.
The coexistence of multiple phases in the domain structure resembles the stationary domain wall in a rotating-squares structure with embedded magnets, showcasing a multistable energy landscape14. Further analysis broadens our perspective, revealing that the trivial solutions correspond to distinct ground states of the system and the soliton solutions represent transition states on an effective energy surface (Figure 1h). Leveraging the continuum model, we extend the concept of multiple degenerate configurations and vector soliton solutions to any distorted lattice. Our analytical predictions offer a convenient method for identifying polarization shifts based on geometric parameters, bypassing the need to calculate phonon bands. Moreover, although we primarily focus on the static character of vector solitons, dynamic responses also showcase the superposition of sub-solitons under a boost.
Our research serves as a catalyst for developing additional models applicable to macroscopic lattices that are analogous to crystal structures. These lattices involve fixed boundaries and connected rotating blocks. This conceptual framework has potential applications in exploring other topological properties experimentally. Additionally, our study reveals the connection between topological lattices and multistable systems, presenting challenges in describing transformable topological systems through geometric insights. Lastly, solitons, which act as robust information carriers, hold promise for topologically protected information processing. The observation of multiple soliton interactions indicates the feasibility of crafting functional devices such soliton-based logic gates, diodes, and algebraic operations in mechanical computing systems.
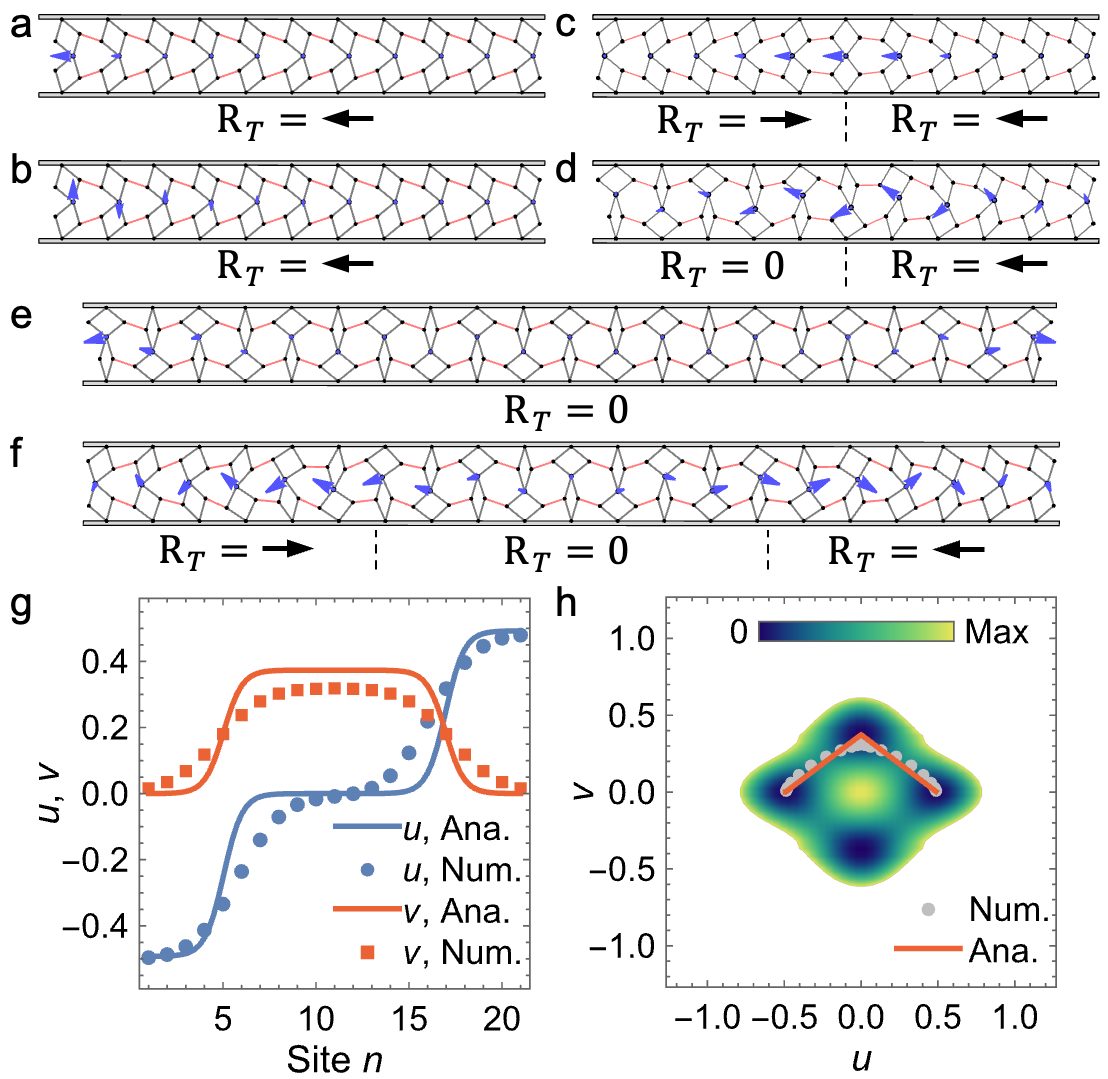
Figure 1. a, b The equilibrium configuration with free boundaries has two independent zero modes localized at the left end, denoted by blue arrows. The calculated topological polarization for the lattice is . c The transformed configuration exhibits a domain wall, interpolating two opposite topological states under an applied perturbation of horizontal zero mode. d The transformed configuration exhibits a domain wall interpolating trivial and nontrivial topological states under an applied perturbation of vertical zero mode. e The trivial configuration with zero mode denoted by blue arrows. f The domain structure separates the trivial regions and different polarized phases. g The distributions of vector soliton within the domain structure exhibit linear combinations of two kink solutions. h The trajectory of the vector soliton is shown in the projection of the effective potential energy density. The vector soliton smoothly interpolates the three ground states. The color bar represents the value of effective potential energy density.
References:
- Yakushevich, L. V., Savin, A. V. & Manevitch, L. I. Nonlinear dynamics of topological solitons in DNA. Phys. Rev. E 66, 016614 (2002).
- Yan, L., Ravasio, R., Brito, C. & Wyart, M. Architecture and coevolution of allosteric materials. Proc. Natl. Acad. Sci. 114, 2526–2531 (2017).
- Rocks, J. W. et al. Designing allostery-inspired response in mechanical networks. Proc. Natl. Acad. Sci. 114, 2520–2525 (2017).
- Noll, N., Mani, M., Heemskerk, I., Streichan, S. J. & Shraiman, B. I. Active tension network model suggests an exotic mechanical state realized in epithelial tissues. Nat. Phys. 13, 1221–1226 (2017).
- Liu, A. J. & Nagel, S. R. The jamming transition and the marginally jammed solid. Annu. Rev. Condens. Matter Phys. 1, 347–369 (2010).
- Lubensky, T. C., Kane, C. L., Mao, X., Souslov, A. & Sun, K. Phonons and elasticity in critically coordinated lattices. Rep. Prog. Phys. 78, 073901 (2015).
- Chen, B. G., Upadhyaya, N. & Vitelli, V. Nonlinear conduction via solitons in a topological mechanical insulator. Proc. Natl. Acad. Sci. 111, 13004–13009 (2014).
- Cheon, S., Kim, T.-H., Lee, S.-H. & Yeom, H. W. Chiral solitons in a coupled double Peierls chain. Science 350, 182–185 (2015).
- Kim, T.-H., Cheon, S. & Yeom, H. W. Switching chiral solitons for algebraic operation of topological quaternary digits. Nat. Phys.13, 444–447 (2017).
- Calladine, C. R. Buckminster Fuller’s “Tensegrity” structures and Clerk Maxwell’s rules for the construction of stiff frames. Int. J. Solids Struct. 14, 161–172 (1978).
- Khare, A. & Saxena, A. Superposed hyperbolic kink and pulse solutions of coupled ϕ4, NLS and mKdV equations. Int. J. Mod. Phys. B 36, 2250142 (2022).
- Deng, B., Raney, J. R., Tournat, V. & Bertoldi, K. Elastic vector solitons in soft architected materials. Phys. Rev. Lett. 118, 204102 (2017).
- Deng, B., Wang, P., He, Q., Tournat, V. & Bertoldi, K. Metamaterials with amplitude gaps for elastic solitons. Nat. Commun. 9, 3410 (2018).
- Yasuda, H., Korpas, L. M. & Raney, J. R. Transition waves and formation of domain walls in multistable mechanical metamaterials. Phys. Rev. Appl. 13, 054067 (2020).
Follow the Topic
-
Communications Physics

An open access journal from Nature Portfolio publishing high-quality research, reviews and commentary in all areas of the physical sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Higher-order interaction networks 2024
Publishing Model: Open Access
Deadline: Feb 28, 2026
Non-Markovian quantum dynamics in physical systems: description and control
Publishing Model: Open Access
Deadline: Dec 31, 2025



Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in
An amazing work about vector solitons in a mechanical system!