The abundance of data about interpersonal relationships, mainly retrieved by harvesting online social platforms, has opened an era in which the validity of social theories can be tested statistically, against benchmarks whose definition is driven by empirical observations. Our contribution focuses on balance theory: firstly proposed by Heider as a psychological theory of behaviour [1], it states that social agents avoid to engage into frustrated configurations shaped by friendly and hostile interactions conflicting with each other. The basic elements of the theory can be represented by adopting the formalism of signed graphs, with positive links representing friendly interactions and negative links representing hostile interactions.

A complete, signed graph is said to be balanced if each triad has an even number of negative edges, i.e. either zero or two. The structure theorem states that a complete, signed graph is balanced if and only if its set of nodes can be partitioned into two, disjoint subsets with positive, intra-modular links and negative, inter-modular links [2]. Cartwright and Harary have, then, extended the definition of balance to incomplete graphs, by including cycles of length larger than three: a network is, now, said to balanced if all cycles have an even number of negative edges [3]. Taken together, the aforementioned criteria define the structural version of the strong balance theory. Later, Davis generalized such a framework, by introducing the concept of k-balanced networks, according to which a signed graph is balanced if its set of nodes can be partitioned into a number k (larger than, or equal to, 2) of disjoint subsets with positive, intra-modular links and negative, inter-modular links [4]. This has led to the formulation of the weak balance theory: a network is, now, said to be balanced if no triad has only one negative edge.

In order to make the strong and the weak variants of the balance theory testable, benchmarks are needed against which comparing the level of frustration characterizing real-world networks. The existing null models, in fact, fail to properly account for the heterogeneity of individual actors, i.e. their different tendencies to establish positive and negative connections. We fill this gap by extending the family of Exponential Random Graphs to binary, undirected, signed networks with both global constraints (overall numbers of positive, negative and missing links) and local constraints (node-specific numbers of positive and negative links); for each type of benchmark, we define two, alternative versions: one where the topology is kept fixed (embodying the situation in which actors can solely choose how to interact) and one where the topology is left free to vary along with the sign of the edges (embodying the situation in which actors can choose how to interact with whom).

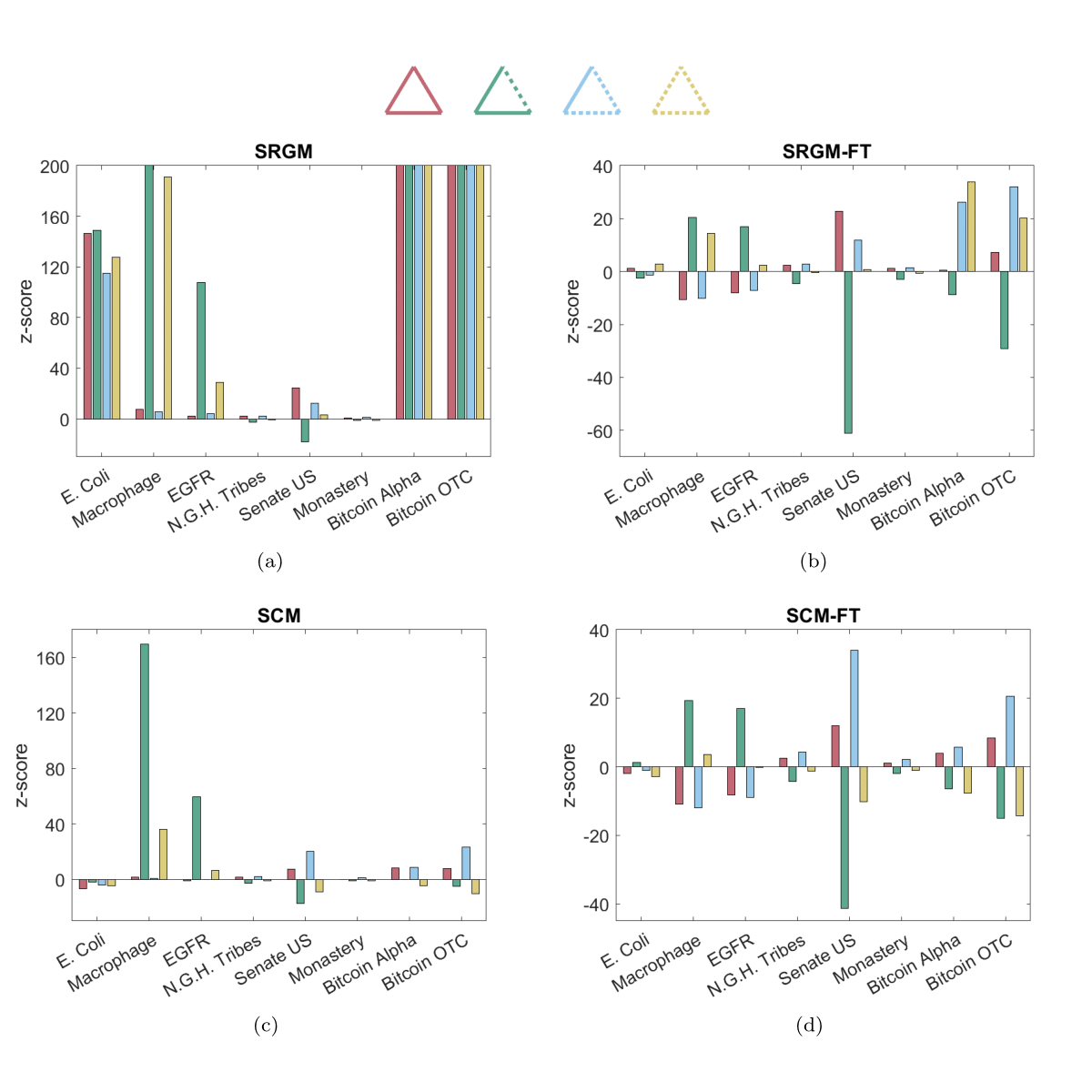
After providing a unified, theoretical framework for analyzing binary, undirected, signed networks, we employ it to evaluate the empirical abundance of the aforementioned, triadic patterns from a statistical perspective. As figure 1 shows, our analysis of three, socio-political networks (N.G.H. Tribes, Senate US, Monastery) and two, financial networks (Bitcoin Alpha, Bitcoin OTC) leads to the following conclusion: i) null models induced by global constraints tend to favour the weak variant of the balance theory, according to which only the triangle with one, negative link (depicted in green) should be under-represented in real-world networks; ii) null models induced by local constraints tend to favour the strong variant of the balance theory, according to which the triangle with three, negative links (depicted in yellow) should be under-represented as well. Instead, biological networks (E. Coli, Macrophage, EGFR) seem to be characterised by a marked tendency towards imbalance.

To sum up, unambiguous conclusions about the theory of balance best supported by data cannot be drawn since an answer like this crucially depends on a number of factors: i) the nature of the data (e.g. biological networks versus social networks); ii) the measure adopted to quantify (im)balance (e.g. weak formulation versus strong formulation); iii) the null model employed to carry out the analysis (e.g. fixed-topology versus free-topology).

1. Heider. The Journal of Psychology 21, 1 (1946).
2. Harary. Michigan Mathematical Journal 2, 2 (1953).
3. Cartwright et al. Psychological Review 63, 5 (1956).
4. Davis. Human Relations 20, 2 (1967).