A team of physicists has taken a fresh look at how black holes “ring” – and their results suggest that tiny deviations from Einstein’s theory of gravity could leave detectable imprints in gravitational waves.

In a new paper in The European Physical Journal C (DOI: 10.1140/epjc/s10052-025-14996-z), Dhruba Jyoti Gogoi, Beyhan Puliçe , and Ali Övgün  explore how a particular kind of black hole behaves in a modified theory of gravity called Symmergent gravity. They focus on two key signatures: quasinormal modes – the tones of the black hole’s ringdown after a disturbance – and greybody factors, which describe how black holes filter the radiation they emit.

Their conclusion: if Symmergent gravity is right, charged black holes should ring and radiate in ways that subtly differ from the predictions of standard general relativity. Those differences might one day be heard by gravitational-wave detectors and seen in black-hole imaging.

Gravity that “emerges” from quantum physics

General relativity explains gravity as the curvature of spacetime, but it doesn’t mesh smoothly with quantum field theory, which successfully describes the other three fundamental forces. Symmergent gravity is an attempt to bridge that gap from a different angle.

In this framework, gravity is not fundamental. Instead, it emerges from the collective behavior of quantum fields once you account properly for high-energy particles and the way they interact with spacetime. The theory naturally generates Einstein’s familiar curvature term, but also predicts an additional curvature-squared term, often written schematically as (R + R^2).

Two parameters play a starring role:

• a quadratic curvature coupling (which is tied to the overall balance between bosons and fermions – including possible dark-sector particles we haven’t yet discovered;

• a vacuum-energy parameter, which encodes how the particle spectrum feeds into the effective cosmological constant.

These parameters act like hidden knobs that slightly reshape the geometry around a black hole.

A charged black hole in Symmergent gravity

The team studies a charged Symmergent black hole – the analogue of a Reissner–Nordström black hole (a charged black hole in Einstein–Maxwell theory), but now in the Symmergent gravity setting.

This object is characterized by:

• its mass (M),

• its electric charge (Q),

• and the two Symmergent parameters (c_0) and (\alpha).

In earlier work, some of the same authors showed how these parameters modify the shadow and photon sphere of the black hole – quantities that can be probed by the Event Horizon Telescope. In the new paper, they ask a dynamical question instead:

If you “hit” this black hole with a disturbance – a wave of matter, light, or ripples in spacetime itself – how does it ring down? And how does it radiate?

Quasinormal modes: the cosmic ringing of spacetime

When two black holes merge, the newly formed object is violently distorted. It then settles down by emitting gravitational waves in a characteristic “ringdown” phase, much like a struck bell. The allowed tones are called quasinormal modes (QNMs).

Each mode has:

• a frequency (pitch),

• and a damping rate (how quickly the tone dies away).

These depend only on the properties of the black hole, not on how it was disturbed. That’s why QNMs are often described as the “fingerprints” of black holes.

Gogoi, Puliçe, and Övgün compute QNMs for three kinds of perturbations:

• scalar (simplified matter fields),

• electromagnetic (light-like disturbances),

• gravitational (true ripples of spacetime).

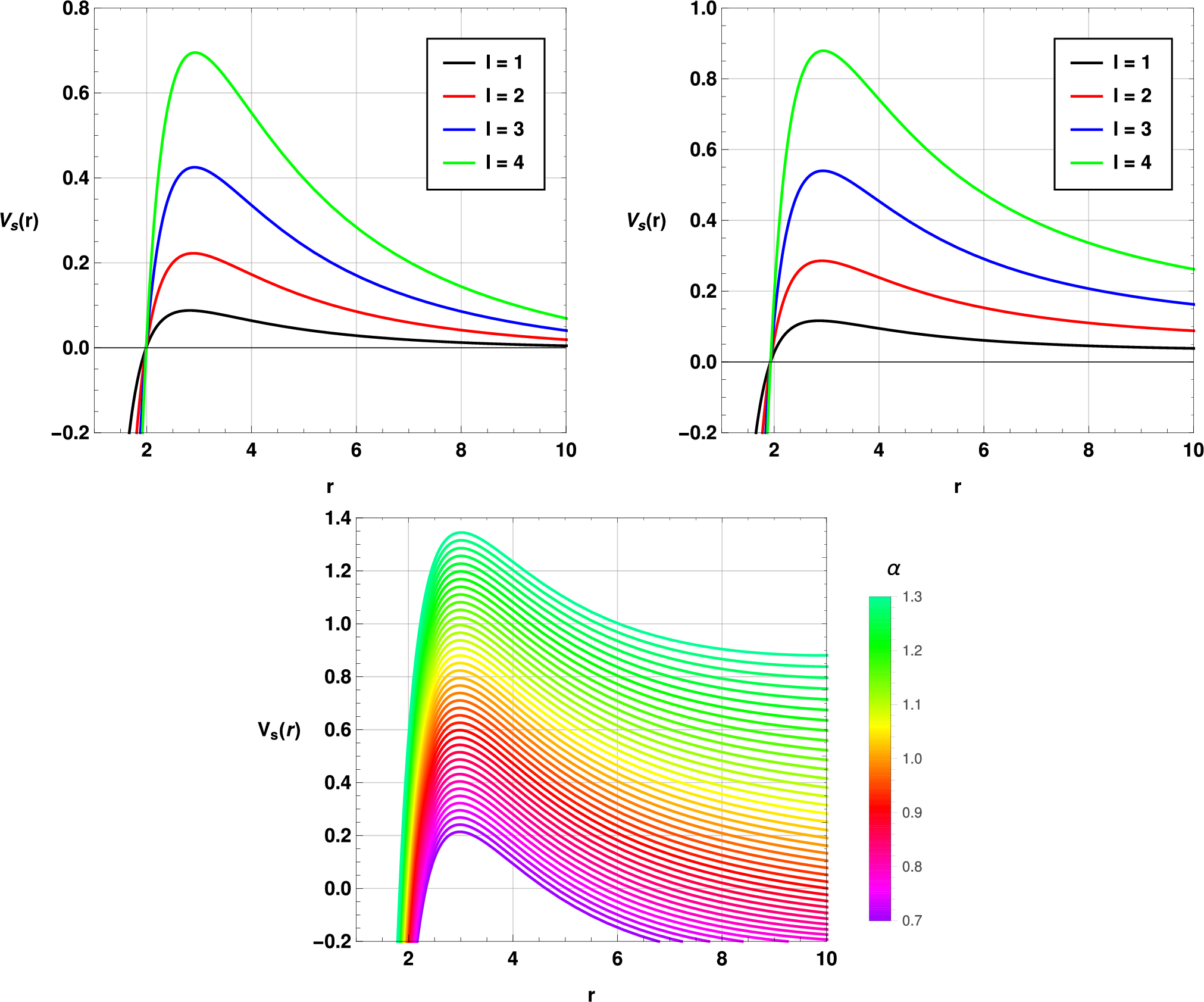
Technically, they do this by turning the perturbation equations into wave equations with an effective potential barrier and using a high-order WKB approximation refined with Padé averaging, cross-checked with time-domain simulations.

What changes when you tune the new knobs?

The authors then systematically vary the Symmergent parameters and the black hole charge to see how the ringdown responds. Some key trends:

• Vacuum-energy parameter (\alpha):
  Increasing (\alpha) makes the black hole ring at higher frequencies and damp faster, and this happens almost linearly. In everyday language: turning up (\alpha) turns the ring into a higher, sharper “ping” that dies out more quickly. This is true for scalar, electromagnetic, and gravitational waves.

• Curvature coupling (c_{\rm O}):
  Its effect is nonlinear and most dramatic when (|c_{\rm O}|) is small. In that regime, both the frequencies and damping rates of the QNMs change rapidly. For large (|c_{\rm O}|), the spectrum tends to saturate and approach behavior similar to standard black holes.

• Charge (Q):
  As the black hole’s charge grows, both the frequency and damping rate increase. A more strongly charged black hole rings faster and settles down more quickly. Interestingly, the pattern is not just a simple copy of the familiar Reissner–Nordström case; the Symmergent corrections add extra structure.

• Type of perturbation:
  For the same parameters, scalar modes tend to have the highest frequencies and fastest decay, electromagnetic modes are intermediate, and gravitational modes are the slowest to damp. That means the “pure” gravitational signal from the black hole lingers the longest.

The team also checks a well-known theoretical bound called Hod’s conjecture, which links the damping rate of the modes to the Hawking temperature. They find it is respected across most of the physically allowed parameter space. Apparent violations occur only in regimes where the approximations themselves become unreliable, near extremal limits.

Greybody factors: how black holes filter radiation

Hawking’s original calculation suggested black holes radiate like perfect black bodies. In reality, the surrounding spacetime acts like a frequency-dependent filter: some modes escape easily, others are partially reflected back. The result is not a pure blackbody spectrum but a “greybody” one.

The greybody factor tells you, for each frequency, how much of the radiation generated near the horizon actually makes it out to infinity. The same effective potentials that govern QNMs also control these transmission probabilities.

The authors show that:

• increasing (\alpha), (c_{\rm O}), or the charge (Q) tends to reduce the greybody factors – the black hole becomes more “reflective” and absorbs less;

• gravitational perturbations typically reach their peak absorption at slightly lower frequencies than scalar and electromagnetic ones;

• the pattern of greybody factors and their rigorous analytic bounds follow the same parameter trends as the QNMs.

Together, the QNM spectrum and greybody factors paint a coherent picture of how charged Symmergent black holes respond to and emit radiation.

Listening for new physics in future data

Why does all this matter? Because gravitational-wave observatories such as LIGO, Virgo, KAGRA and future detectors like LISA can, in principle, measure black hole ringdowns with increasing precision. At the same time, black-hole images and spectra from facilities like the Event Horizon Telescope and JWST probe the near-horizon region in complementary ways.

If real astrophysical black holes follow exactly Einstein’s equations, their QNM frequencies and damping times must lie along very specific curves. Symmergent gravity predicts small but systematic deviations controlled by (\alpha), (c_{\rm O}), and (Q).

In other words, by carefully “listening” to how black holes ring and by studying how they filter radiation, future observations could either:

• find no deviations – tightening the bounds on these new parameters and on the underlying particle content of the universe,
  or

• reveal anomalies that might be the first hints that gravity truly emerges from a deeper quantum structure.

For now, the charged Symmergent black hole remains a theoretical laboratory. But as our cosmic ears become more sensitive, the echoes it predicts might help answer one of physics’ oldest questions: what is gravity, really?