A computationally simple approach (i.e., the PSK method) for solving fully intuitionistic fuzzy real-life transportation problems
Published in Mathematics and Business & Management

More details on this study can be found in our recent article "Computationally simple approach for solving fully intuitionistic fuzzy real life transportation problems" published in International Journal of System Assurance Engineering and Management (https://doi.org/10.1007/s13198-014-0334-2).
In tackling real-world transportation problems, people frequently encounter uncertainty and hesitancy due to a variety of unpredictable factors. So, to deal with impreciseness and reluctance, numerous authors have proposed an intuitionistic fuzzy representation of the data. So, in this study, the authors look at a transportation problem with uncertainty and reluctance in all its parameters. The authors outline the issue and use triangular intuitionistic fuzzy numbers (TrIFNs) to address uncertainty and hesitation. The authors offer a new method, the PSK method, for finding the intuitionistic fuzzy optimal solution to the fully intuitionistic fuzzy transportation (FIFTP) issue in one stage. Additionally, a novel multiplication operation on TrIFN is presented to determine the minimum objective value in terms of TrIFN. In actual life, the type-4 IFTP has a wide range of uses, including satellite/missile launch and oil delivery. So there is no question that this article will fascinate everyone if they read it.
The fundamental advantage of this method is as follows:
- Computationally simple and easy to understand
- It gives physically meaningful objective function value
- It is a one-stage method
- It is independent of the initial solution
- It has a smaller number of steps
- It solves the real-life problem
- The PSK method is efficient and always gives optimal solutions. Since the authors have theoretically demonstrated it.
In the literature, the author P. Senthil Kumar (PSK) originally divided IFTPs into four categories, namely, type-1, 2, 3, and 4. He solved all four types of problems using various methods with software, including the PSK method. This article deals with full/type-4 IFTP. Studying IFTP is better than studying fuzzy transportation problems (FTPs)1, 2. From the FTPs, we can determine the acceptance of the transportation cost, but we cannot determine the degree of non-acceptance and degree of hesitation of the transportation cost3, 4. For more details, see here5.
In our day-to-day lives, there is a need to ship commodities from various factories to various warehouses6. Understanding the transportation issue is critical to effectively managing this situation. However, transportation cost, demand, and supply are not exact values due to unpredictable circumstances7, 8. As a result, resolving transportation issues with intuitionistic fuzzy number is more critical. So, this work effectively resolves the type-4 IFTP. We can read about comparable situations with different approaches and different constraints here9, 10. Table 1 compares the proposed study to existing literature.
Table 1 Comparison study
| Problem No. | Ranking method | Solution Method | Solution Method | Solution Method | Solution Method | Solution Method |
|
VAM |
MODI |
Zero Point Method |
Intuitionistic Fuzzy Zero Point Method |
PSK Method |
||
|
1 |
Annie Varghese and Sunny Kuriakose |
391 |
391 |
391 |
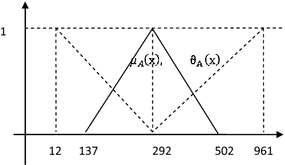
(137,292,502)(12,292,961) 391 |
(137,292,502)(12,292,961) 391 |
|
2 |
Annie Varghese and Sunny Kuriakose |
118 |
118 |
118 |
(77,118,159)(42,118,194) 118 |
(77,118,159)(42,118,194) 118 |
Fig. 1 shows the graphical representation of intuitive fuzzy transportation cost.
Fig. 1 Graphical representation of intuitive fuzzy transportation cost
References:
- Kumar, P.S. PSK method for solving type-1 and type-3 fuzzy transportation problems. Int J Fuzzy Syst Appl 5(4):121–146, https://doi.org/10.4018/IJFSA.2016100106, (2016).
- Kumar, P.S. Search for an optimal solution to vague traffic problems using the PSK method. Handbook of Research on Investigations in Artificial Life Research and Development, IGI Global, pp. 219–257, https://doi.org/10.4018/978-1-5225-5396-0.ch011, (2018).
- Kumar, P.S. The PSK Method: A new and efficient approach to solving fuzzy transportation problems. Transport and Logistics Planning and Optimization, IGI Global, pp. 149–197, https://doi.org/10.4018/978-1-6684-8474-6.ch007, (2023).
- Kumar, P.S. A simple method for solving type-2 and type-4 fuzzy transportation problems. Int J Fuzzy Logic Intell Syst 16(4):225–237, https://doi.org/10.5391/IJFIS.2016.16.4.225, (2016).
- Kumar, P.S. Algorithms for solving the optimization problems using fuzzy and intuitionistic fuzzy set. Int J Syst Assur Eng Manag 11(1):189–222, https://link.springer.com/10.1007/s13198-019-00941-3, (2020).
- Kumar, P. S. Algorithms and software packages for solving transportation problems with intuitionistic fuzzy numbers. Operational Research for Renewable Energy and Sustainable Environments, IGI Global, pp. 1–55, https://doi.org/10.4018/978-1-6684-9130-0.ch001, (2023).
- Hussain, R.J, Kumar, P.S. An optimal more-for-less solution of mixed constraints intuitionistic fuzzy transportation problems. Int J Contemp Math Sci 8:565–576, https://doi.org/10.12988/ijcms.2013.13056, (2013).
- Kumar, P.S, Hussain, R.J. A systematic approach for solving mixed intuitionistic fuzzy transportation problems. Int J Pure Appl Math 92:181–190, https://doi.org/10.12732/ijpam.v92i2.4, (2014).
- Kumar, P.S, Hussain, R.J. A simple method for solving fully intuitionistic fuzzy real life assignment problem. Int J Oper Res Inf Syst 7(2):39–61, https://doi.org/10.4018/IJORIS.2016040103, (2016).
- Kumar, P.S. A note on ‘a new approach for solving intuitionistic fuzzy transportation problem of type-2’. Int J Logist Syst Manag 29(1):102–129, https://doi.org/10.1504/ijlsm.2018.10009204; https://doi.org/10.1504/ijlsm.2018.088586, (2018).
Follow the Topic
-
International Journal of System Assurance Engineering and Management

This Journal is established with a view to cater to increased awareness for high quality research in the seamless integration of heterogeneous technologies to formulate bankable solutions to the emergent complex engineering problems.




Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in