More details on this study can be found in our recent article "Intuitionistic fuzzy solid assignment problems: a software-based approach" published in International Journal of System Assurance Engineering and Management (https://doi.org/10.1007/s13198-019-00794-w).

Two kinds of constraint sets—job and machine constraints—are taken into consideration in a traditional assignment problem (AP). But in addition to these two constraint sets, the author also deals with a third kind of constraint set in his daily life, which is referred to as a factory constraint. The third constraint, the factory constraint, results from various assignment modes (conveyances). In this instance, the assignment problem becomes a solid assignment problem (SAP). As a result, the idea of researching SAP is one of the most interesting in mathematical history. It is significant in real-world circumstances as well. In the literature, several academicians have proposed several algorithms to address this problem.

In general, the time it takes each machine in a factory to execute a task varies, for example, due to unplanned power interruptions and variations. Furthermore, each job's completion time varies from factory to factory based on the productivity of the machine or the skill of the workers. As a result, it is difficult to predict when each task will be completed on each machine across various factories. Thus, we must apply fuzzy set theory to deal with imprecise information^{1, 2}. However, the fuzzy set deals with membership values and doesn't consider non-membership values and hesitation index^{3, 4, 5}. It is the major disadvantage of the fuzzy set. So, in this study, the authors look at an assignment problem with uncertainty and reluctance in its parameter. The author outlines the issue and uses triangular intuitionistic fuzzy numbers (TIFNs) to address uncertainty and hesitation. The author offers a new software-based approach for finding the optimal solution to the IFSAP. Additionally, both the IFSAP and its conventional problem solutions are obtained simultaneously. IFSAPs are widely used in organizations and businesses in our daily lives. Therefore, it is certain that everyone who reads this post will find it fascinating.

The following are this approach's primary benefits:

1.  It is independent of existing intuitionistic fuzzy methods.
2.  It provides an optimal solution with a smaller number of steps and reduces the decision-  maker's computational time as well.
3.  It is useful to solve unbalanced, balanced, maximization, minimization, intuitionistic fuzzy,   fuzzy, and crisp AP.
4.  It helps solve complex problems, and sensitivity analysis is also possible.
5.  This approach always yields the best and most reliable solution, i.e., the optimal solution,   because the author has proved the necessary theorems.

In the literature, the author P. Senthil Kumar (PSK) originally divided IFAPs into two categories, namely, mixed and full IFAPs^{6, 7, 8}. He solved all two types of problems using various software methods, including the PSK method. This article deals with full IFSAP. Studying full IFSAP is better than studying fuzzy assignment problems (FAPs). From the FAPs, we can determine the acceptance of the assignment cost/time, but we cannot determine the degree of non-acceptance and degree of hesitation of the assignment cost/time. For more information, see here^{9, 10, 11}.

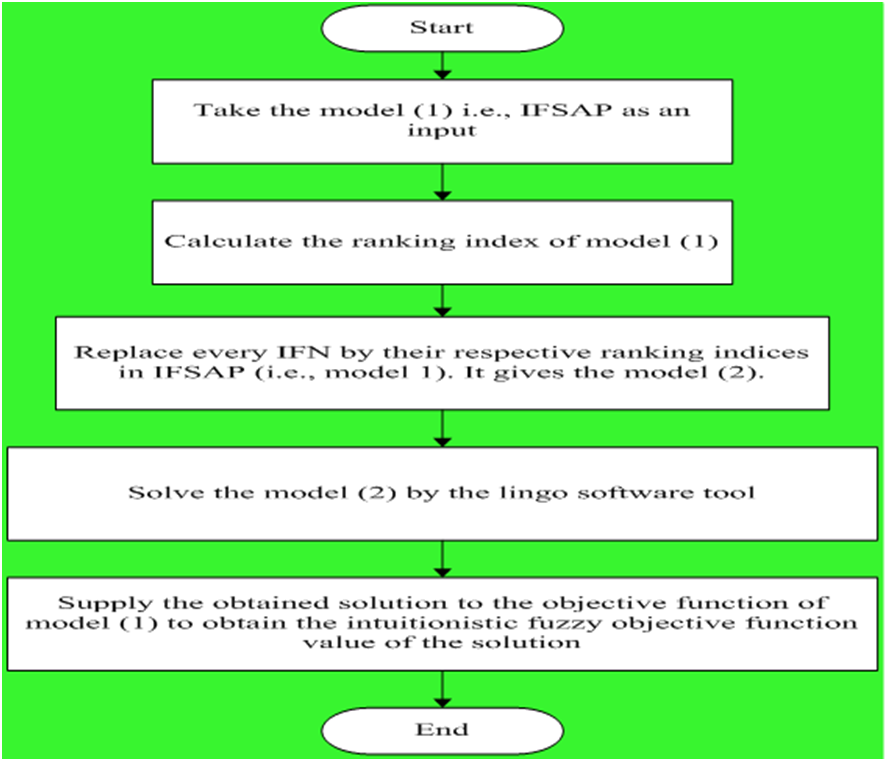
In our daily lives, there is a need to assign resources economically. Understanding the assignment issue is critical to effectively managing this situation. However, because of unforeseen environments, assignment cost/time is not a crisp number¹². As a result, resolving assignment issues with intuitionistic fuzzy numbers is more critical. So, this work effectively resolves the full IFSAP. We can learn about similar problems with different approaches and limits here^{13, 14, 15}. Fig. 1 shows the flowchart of the suggested technique for IFSAP.

Fig. 1 The flowchart of the proposed method for IFSAP

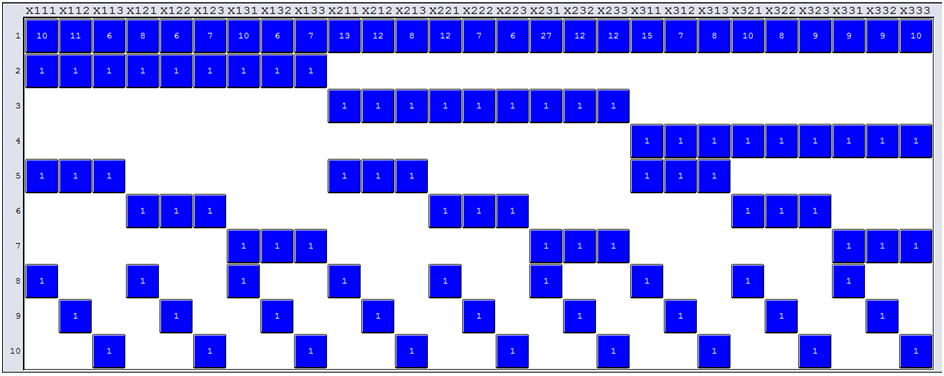
The Lingo matrix picture for the conventional SAP corresponding to the given IFSAP is given in Fig. 2.

Fig. 2 Lingo matrix picture for the conventional SAP corresponding to the given IFSAP

References:

1. Kumar, P. S. PSK method for solving type-1 and type-3 fuzzy transportation problems. Fuzzy Systems: Concepts, Methodologies, Tools, and Applications, IGI Global, pp. 367–392, https://doi.org/10.4018/978-1-5225-1908-9.ch017, (2017).
2. Kumar, P.S. A simple method for solving type-2 and type-4 fuzzy transportation problems. Int J Fuzzy Logic Intell Syst 16(4):225–237, https://doi.org/10.5391/IJFIS.2016.16.4.225, (2016).
3. Kumar, P. S. Algorithmic approach for solving allocation problems under intuitionistic fuzzy environment [PhD thesis]. Jamal Mohamed College, Tiruchirappalli, India, http://hdl.handle.net/10603/209151; https://shodhganga.inflibnet.ac.in/handle/10603/209151, (2015).
4. Kumar, P.S, Hussain, R.J. Computationally simple approach for solving fully intuitionistic fuzzy real life transportation problems. Int J Syst Assur Eng Manag 7:90–101, https://link.springer.com/10.1007/s13198-014-0334-2, (2016).
5. Kumar, P. S. PSK method for solving mixed and type-4 intuitionistic fuzzy solid transportation problems. Int J Oper Res Inf Syst 10(2):20–53, https://doi.org/10.4018/ijoris.2019040102, (2019).
6. Kumar, P.S, Hussain, R.J. A simple method for solving fully intuitionistic fuzzy real life assignment problem. Int J Oper Res Inf Syst 7(2):39–61, https://doi.org/10.4018/IJORIS.2016040103, (2016).
7. Kumar, P. S. Ai-driven decision support system for intuitionistic fuzzy assignment problems. Using Traditional Design Methods to Enhance AI-Driven Decision Making, IGI Global, pp. 352–398, https://doi.org/10.4018/979-8-3693-0639-0.ch016, (2024).
8. Kumar, P. S. The PSK method for solving fully intuitionistic fuzzy assignment problems with some software tools. Theoretical and Applied Mathematics in International Business, IGI Global, pp. 149–202, https://doi.org/10.4018/978-1-5225-8458-2.ch009, (2020).
9. Kumar, P.S. Algorithms for solving the optimization problems using fuzzy and intuitionistic fuzzy set. Int J Syst Assur Eng Manag 11(1):189–222, https://link.springer.com/article/10.1007/s13198-019-00941-3, (2020).
10. Kumar, P.S. An efficient approach for solving type-2 intuitionistic fuzzy solid transportation problems with their equivalent crisp solid transportation problems. Int J Syst Assur Eng Manag 15(9):4370–4403, https://doi.org/10.1007/s13198-024-02433-5, (2024).
11. Kumar, P. S. A simple and efficient algorithm for solving type-1 intuitionistic fuzzy solid transportation problems. Int J Oper Res Inf Syst 9(3):90–122, https://doi.org/10.4018/ijoris.2018070105, (2018).
12. Kumar, P. S. Developing a new approach to solve solid assignment problems under intuitionistic fuzzy environment. Int J Fuzzy Syst Appl 9(1):1–34, https://doi.org/10.4018/ijfsa.2020010101, (2020).
13. Kumar, P.S. Computationally simple and efficient method for solving real-life mixed intuitionistic fuzzy 3D assignment problems. In J Softw Sci Comput Intell 14(1):1–42, https://doi.org/10.4018/IJSSCI.291715, (2022).
14. Kumar, P.S. PSK method for solving intuitionistic fuzzy solid transportation problems. Int J Fuzzy Syst Appl 7(4):62–99, https://doi.org/10.4018/ijfsa.2018100104, (2018).
15. Kumar, P. S. Theory and applications of the software-based PSK method for solving intuitionistic fuzzy solid assignment problems. Applications of New Technology in Operations and Supply Chain Management, IGI Global, pp. 360–403, https://doi.org/10.4018/979-8-3693-1578-1.ch019, (2024).