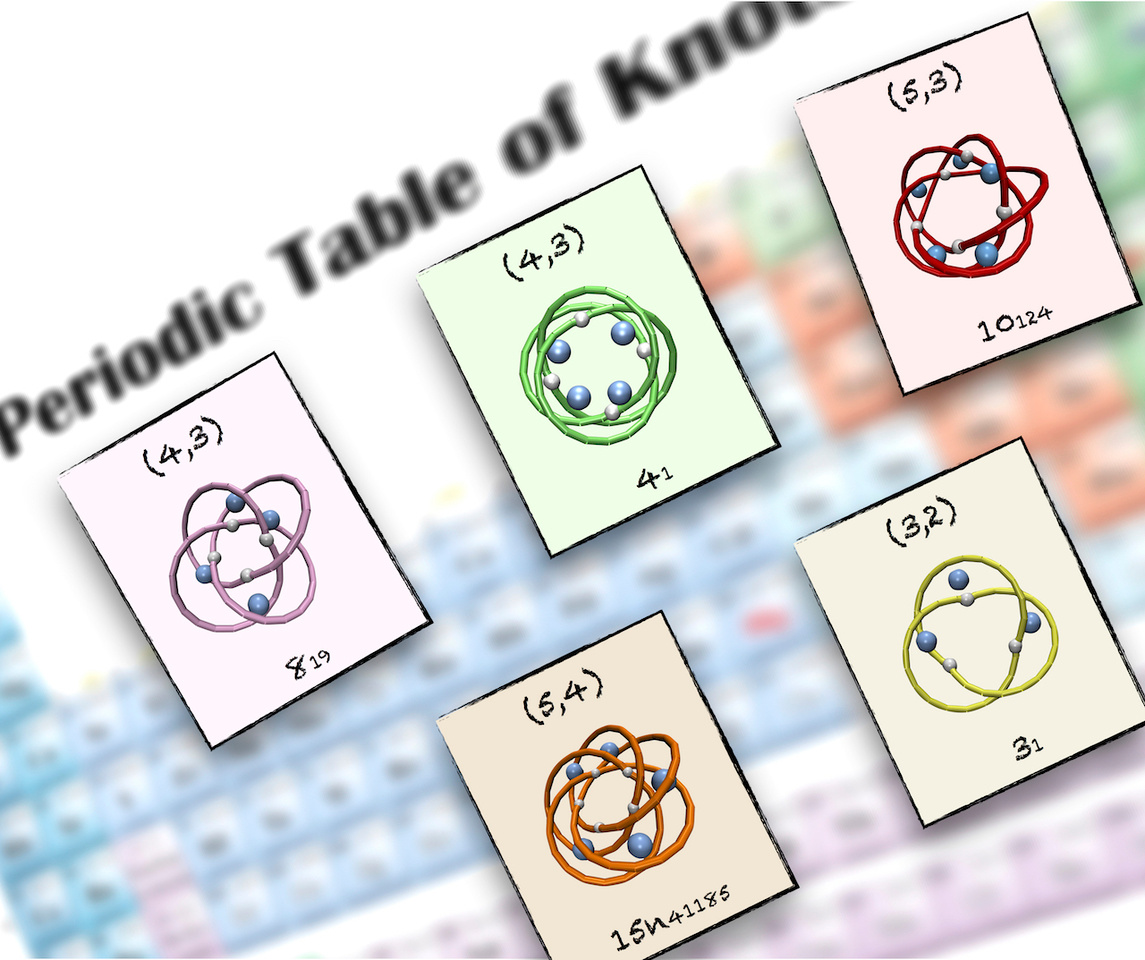
This blog refers to the newly-published Nat. Commun. paper by Marenda et al. available here.

Until a couple of years ago, very few types of molecular knots had been synthesised: the trefoil, the figure-of-eight and the pentafoil knots.

These are also the simplest knot types, featuring respectively 3, 4 and 5 projected crossings in their simplest geometrical representations.

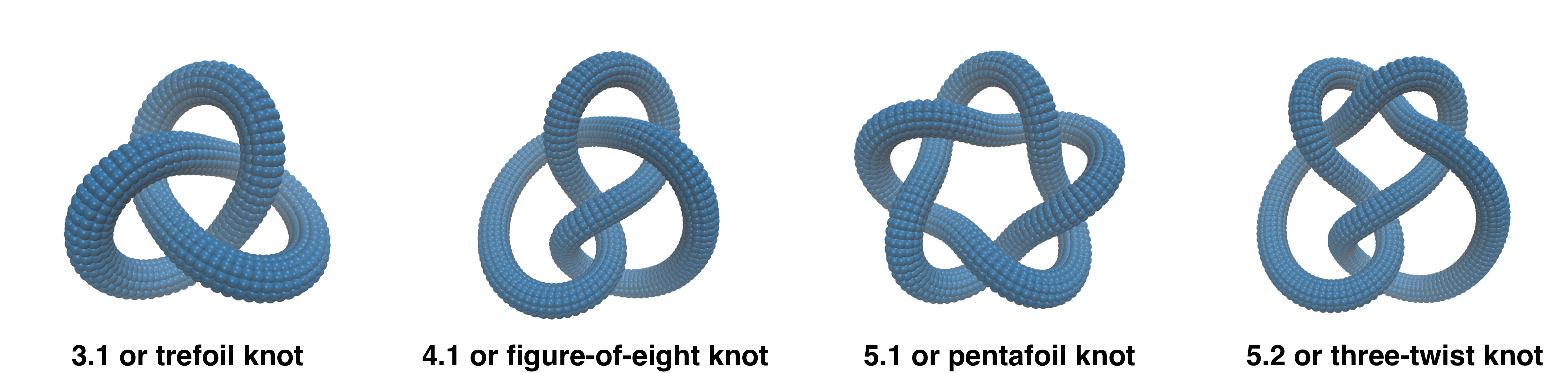
 At that time it could have appeared plausible that the next topology to be discovered would have been the three-twist or stevedore knots, which are the next rungs on the ladder of knot complexity.

But our previous experience with models of DNA and flexible polymers suggested a possible alternative scenario, because certain knot types are  entropically favoured over others with same, or even higher complexity. For instance, a three-twist knot is twice more likely to appear in an equilibrated flexible polymer than a pentafoil knot, though the minimal crossing number is 5 for both knots.

How would these entropic differences play out for molecular knots and their synthesis by self-assembly? Would their kinetic and thermodynamic accessibility follow the canonical complexity ranking or would they subvert it?

We first addressed these questions in a 2015 Nat. Commun. paper that motivated the current investigation. In that study we simulated monodispersed solutions of  helical templates, mimicking the helicates used experimentally, and found that the most accessible topologies were essentially two [1].

The first was trefoil knot, whose innate propensity to self-assemble is illustrated in this video demonstration of a trefoil knot that self-assembles from 3D-printed elements. 

The other accessible topology was the 8.19 knot [1]. This came as a big surprise because, with its eight crossings in the minimal projection, the 8.19 knot largely surpassed in complexity any knot that had been realised before. The prediction was proven correct when the breakthrough realisation of the 8.19 molecular knot was reported[2].

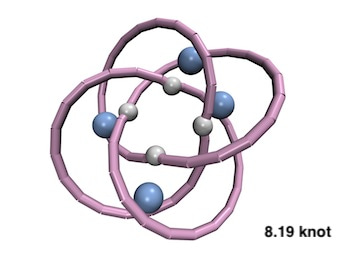
The results reinforced our idea that certain topologies are much more accessible than others and hence also amenable to be discovered with simplified models. 

We therefore embarked on the systematic search of additional privileged topologies that is reported in a newly-published Nat. Commun. paper [3].

This expanded survey, as we quickly found out, could not be achieved by simply increasing the size of the simulated system, the concentration of helical templates in solution, or the duration of the self-assembly simulations. The law of mass action, in fact, was an insurmountable barrier towards sampling knots of increasing complexity made of large numbers of templates. 

We therefore circumvented this problem by using a Monte Carlo scheme to explore the large conformational space of constructs made of a preassigned number of templates. Then, a posteriori, we focussed on those conformers that had the hallmark geometric features found in actual molecular knots, namely quasi-planarity and cyclic-symmetry. This two-tier scheme, besides recovering known types of molecular knots, returned two novel privileged topologies, respectively with 10 and 15 minimal crossings. The results were also corroborated by MD simulations using both templates and attractive coordinating particles.

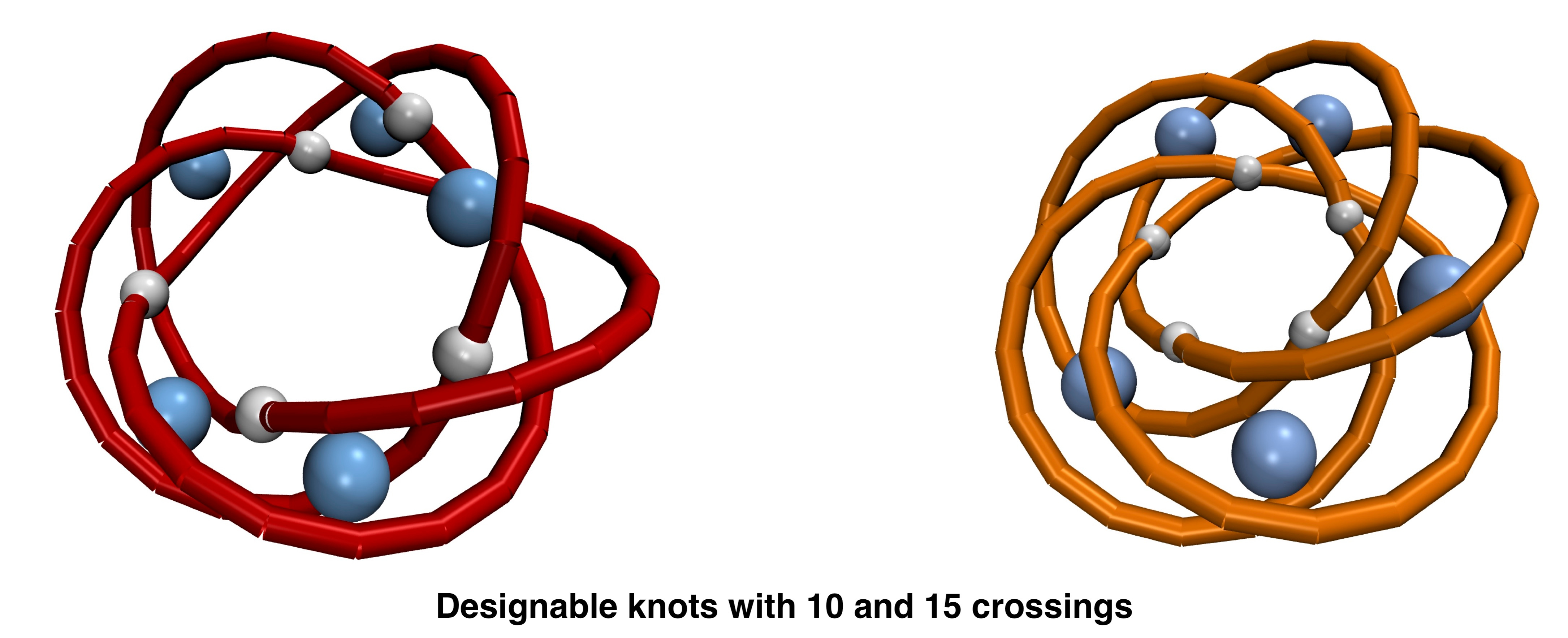
One afternoon, when making drawings of these structures, Mattia Marenda, PhD student and first author of the latest Nat. Commun. study [3], noticed that the linear braid representation of these knots followed particularly simple repetitive patterns.

We then spent the rest of the day at the blackboard discussing the relevant parameters that appeared ideally suited to organize the repertoire of designable molecular knots. We eventually settled for two: the number of templates and the number of strands in the braid representation, which capture different aspects of the expected difficulty of realisation.

This step proved crucial to generalise the earlier results of Monte Carlo and self-assembly simulations. The two-parameter classification was providing a chart, a kind of “periodic table”, which organises not only all known molecular knots but also new privileged topologies that have not been realised yet.

These as-yet-undiscovered topologies include complex links and catenanes, and one can imagine that future breakthroughs may involve these fascinating types of multi-component knots. We speculate that as the repertoire of realisable self-assembling molecular knots increases, possibly thanks to the use of new shapes of their building blocks, so will the interest and motivation to find applicative avenues. At present, a promising one is their potential as vectors of nano-cargos that could be loaded and released under specific physico-chemical conditions. 

References

1. Polles, G., Marenduzzo, D., Orlandini, E. and Micheletti, C.
   Self-assembling knots of controlled topology by designing the geometry of patchy templates.
   Nat. Commun. 6, 6423 (2015). 
2. J.J. Danon, A. Krüger, D.A. Leigh, J. Lemonnier, A.J. Stephens, I.J. Vitorica-Yrezabal and  S. L. Woltering 
   Braiding a molecular knot with eight crossings.
   Science 355, 159–162 (2017).
3. M. Marenda, E. Orlandini and C. Micheletti, 
   Discovering privileged topologies of molecular knots with self-assembling models. 
   Nat. Commun. 9, 3051 (2018).