In biological systems, there are many examples of robust behavior emerging from dimensionality reduction. The state space of all possible biochemical reactions can be complicated and high-dimensional, while the observed behavior reduces to a much smaller state space. For example, computational models of memory describe specific attractor states in the firing of neurons, which represent persistent memories. Another example is long oscillations such as circadian rhythms, which follow well-defined sequences of reactions in each cycle. Such low-dimensional dynamics can be highly robust. They persist over a long time without obvious attenuation, even though the underlying reactions are intrinsically stochastic and tend to lose accuracy over time. It is crucial to understand the principles that lead to such robustness, as their disruption can lead to adverse health effects and reduced reproductive fitness for many organisms.

Robust dynamics from topology

In the study of quantum materials, one mechanism for generating robust dynamics in a lower dimension is topological protection. Generalized to stochastic systems, topology describes whether distinct chemical configurations have a global pattern of transition rates between them that supports edge states. Powerfully, such edge dynamics are insensitive to various types of noise and disorder. Even when there are missing pieces in the chemical state space, the edge currents keep going around the new boundary, as shown in Figure 1.

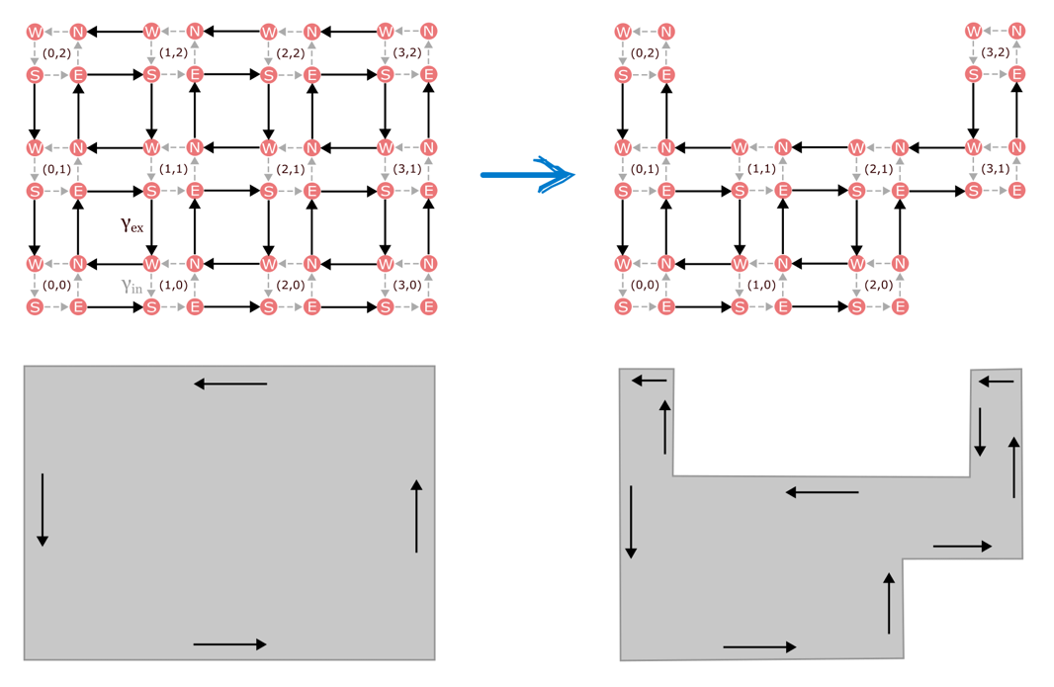
Figure 1. In the presence of missing model components, edge states propagate along the new boundary.

Given the many attractive properties from topological protection, it would be highly desirable to demonstrate how it can be realized in a biological setting. Topologically protected dynamics has been observed in mechanical, photonic, and many other systems, but has yet to be shown to relate to a stochastic biological system. Our work responds to this lack in the field, by providing detailed biophysical mechanisms to obtain topological dynamics in bacterial circadian rhythm.

A topological model for circadian rhythm

Specifically, we propose a topological model for the KaiABC system, a group of three proteins (KaiA, KaiB, KaiC) that regulates circadian rhythm in cyanobacteria. The KaiC protein maintains a 24-hour phosphorylation cycle, modulated by the interaction with KaiA and KaiB. In vitro, the phosphorylation cycle can maintain a 24-hour period for many days even in a dark room with no daylight cues.

KaiC exists in solution as hexamers. Each monomer in the hexamer has two phosphorylation sites, T and S. As shown in Figure 2a, KaiC goes through a very specific phosphorylation sequence: all six T sites get phosphorylated first, followed by the S sites. Then, all T sites get dephosphorylated, again followed by the S sites. It is surprising that KaiC dynamics goes through this specific sequence in a robust manner, given that KaiC monomers can phosphorylate independently in T or S.

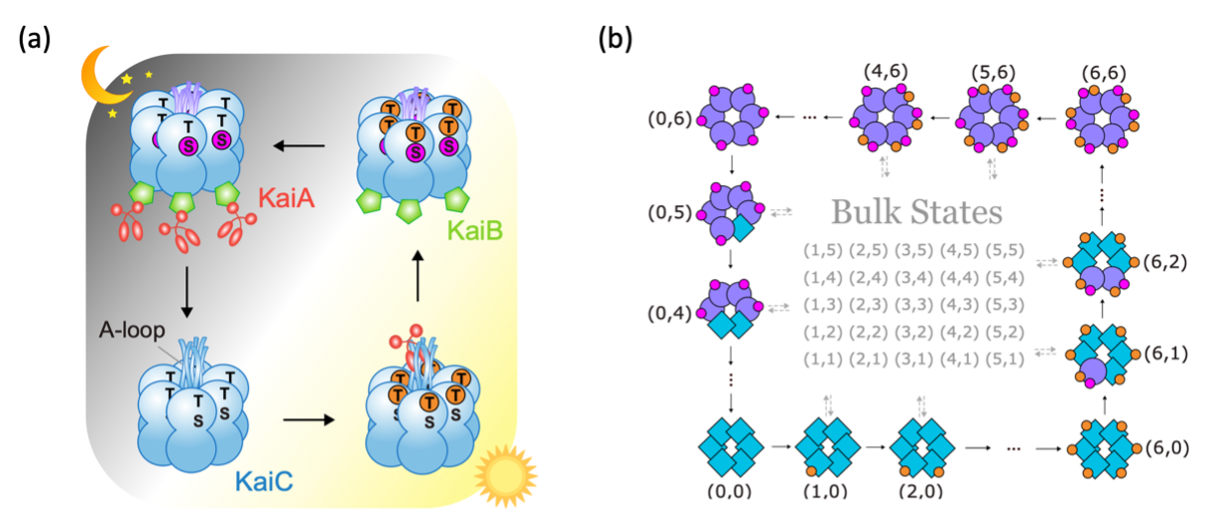
Figure 2. (a) Circadian rhythm in cyanobacteria is sustained by phosphorylation/dephosphorylation cycles of KaiC hexamers. (b) Edge dynamics in our topological model reproduces the specific sequence of KaiC phosphorylation cycle.

Our topological model for the KaiABC system takes inspiration from “futile cycles” in biology, which are out-of-equilibrium reaction cycles that consumes energy but does not seem to change the system in any other way. We propose that single KaiC molecules go through such dissipative reaction cycles, which is the basic motif in our model. Such reaction cycles are repeated for each monomer and forms a lattice structure in state space.

This model turns out to host a topological regime, which supports protected edge currents. In other words, the system tends to propagate along the edge of the state space and rarely enter the bulk. The edge dynamics provides a natural explanation for the specific sequence of KaiC phosphorylation in each cycle (Figure 2b). Moreover, the dynamics is effectively reduced to the lower-dimensional boundary of the two-dimensional state space.

A clock that becomes more precise with less energy input

To have any sustained oscillations, the system must be driven out of equilibrium. This requires a consistent free energy input, e.g., from ATP hydrolysis. Increasing the thermodynamic driving from the ATP can generally suppress the stochastic noise and lead to more coherent oscillations. The increased precision, however, is often accompanied by increased energy consumption.

Surprisingly, our topological model supports a novel regime where coherence can increase even as the free energy cost decreases. This unusual phenomenon has a topological origin, as the energy consumption is localized on the edge instead of within the bulk of the state space. Because there are much fewer chemical reactions to consume energy on the edge than in the bulk, the localization leads to an overall decrease in the energetic cost.

A design principle for robust dynamics

By rigorously embedding topological methods within non-equilibrium statistical physics, our work generalizes their usage for various biological and chemical systems. Our results suggest a new mechanism that utilizes dissipative cycles to produce emergent oscillations or attractor states in biological systems. Even though we have mostly discussed our model in the context of the KaiABC system, the model is more general. For example, it can also be mapped to a model of cytoskeletal polymers with cycles of growth and shrinkage. More broadly, our model provides a blueprint for the design of synthetic oscillators – engineered biological clocks that remain precise across different parameter regimes and changing environments. Such robust oscillators provide a powerful tool for accurate timekeeping, which can aid in automation of daily drug delivery, treatment of circadian rhythm disorders, and other potential innovations in medicine and beyond.