For the last decade, the FLUMACS  group has been involved in developing the mesoscale picture of complex fluids, working on problems such as the nucleation of bubbles, their coalescence, and collapse. All these phenomena are characterized by the presence of an interface experiencing topological transitions. At a mesoscale level, depending upon the system of interest, different energy contributions emerge from the microscale details. For example, the interface of liquid/vapor systems is endowed with the sole surface tension, while the presence of amphiphilic molecules yields additional elastic contributions.

Biological membranes, such as the cell membrane, are formed by a fluid bilayer of lipids, amphiphilic molecules with an hydrophilic head and (typically) two hydrophobic tails. This double nature allows the self-assembly of the membrane when lipids are exposed to water. The lipid heads face the aqueous environment, whereas the tails of two different lipid molecules face each other to form the interior of the membrane, which is therefore a "lipid bilayer" to all effects (5 nm thick). In this way the aqueous environment is divided into two parts, e.g. the cytoplasm of the cell and the extracellular fluid, giving the membrane the essential role of barrier. Membranes must also be able to deform, a property for example necessary for red blood cells to flow in narrow capillaries.

Fusion and fission events of fluid lipid membranes are fundamental processes for cell life. For example, they are required for endo- and exocytosis, for viral infections, or to enable neurotransmitters to cross neural synapses. Stability of the membrane with respect to such events of topology change is a necessary prerequisite for their barrier function and for the complex cellular clockworks. Therefore, topological transitions involve high activation energies and must be driven by external agents, e.g. fusion and fission protein machinery.

Inspired by the idea that fusion and fission proteins could have evolved in Nature in order to carry out a minimal work expenditure, in the linked paper, we evaluate the minimal free energy pathway for the transition between two spherical large unilamellar vesicles and a dumbbell-shaped one. From the technical point of view, the breakthrough consists in using a Ginzburg-Landau type of free energy that allows us to describe without interruption the whole, full-scale topological change. Indeed, the classical mechanical description of fluid lipid membranes is based on the celebrated Canham-Helfrich model, which possesses undeniable merits except the ability to deal with topological transitions, unless cuts are artificially made in the sharp elastic surface representing the membrane. Alternatively, muscular approaches such as molecular dynamics, even in its coarse-grained versions, provide invaluable microscopic insight but, for the forthcoming years, they will not yet be able to afford the full-scale simulation of the topological transitions in large and giant vesicles.

The approach we propose considers the membrane as a diffuse interface and, in the limit of small width-to-vesicle-extension ratio (sharp interface limit), the Ginzburg-Landau free energy approaches the Canham-Helfrich one.  This strategy allows us to uniquely compute the force fields needed to drive the topological change along the minimal free energy pathway, therefore with minimal work expenditure. The forces take into account the subtle effects induced by the Gauss-Bonnet theorem of differential geometry, which quantizes the Gaussian energy term of the asymptotic Canham-Helfrich model. The computed forces are in excellent agreement in terms of intensity, scale, and spatial localization with experimental data on typical fission protein systems, like the ESCRT-III, FtsZ, and dynamin.  Furthermore, our results suggest that fusion proteins, besides a direct mechanical action, may also locally modify the (Gaussian) rigidity of the membrane. Indeed, we find that the activation energy of the fusion process is associated with a very steep free energy profile making it mainly topological. On the contrary, the activation energy of the fission process is due to the deformation that the membrane must undergo to create a small neck where the division takes place. This makes the two processes physically different, even if topologically inverse.

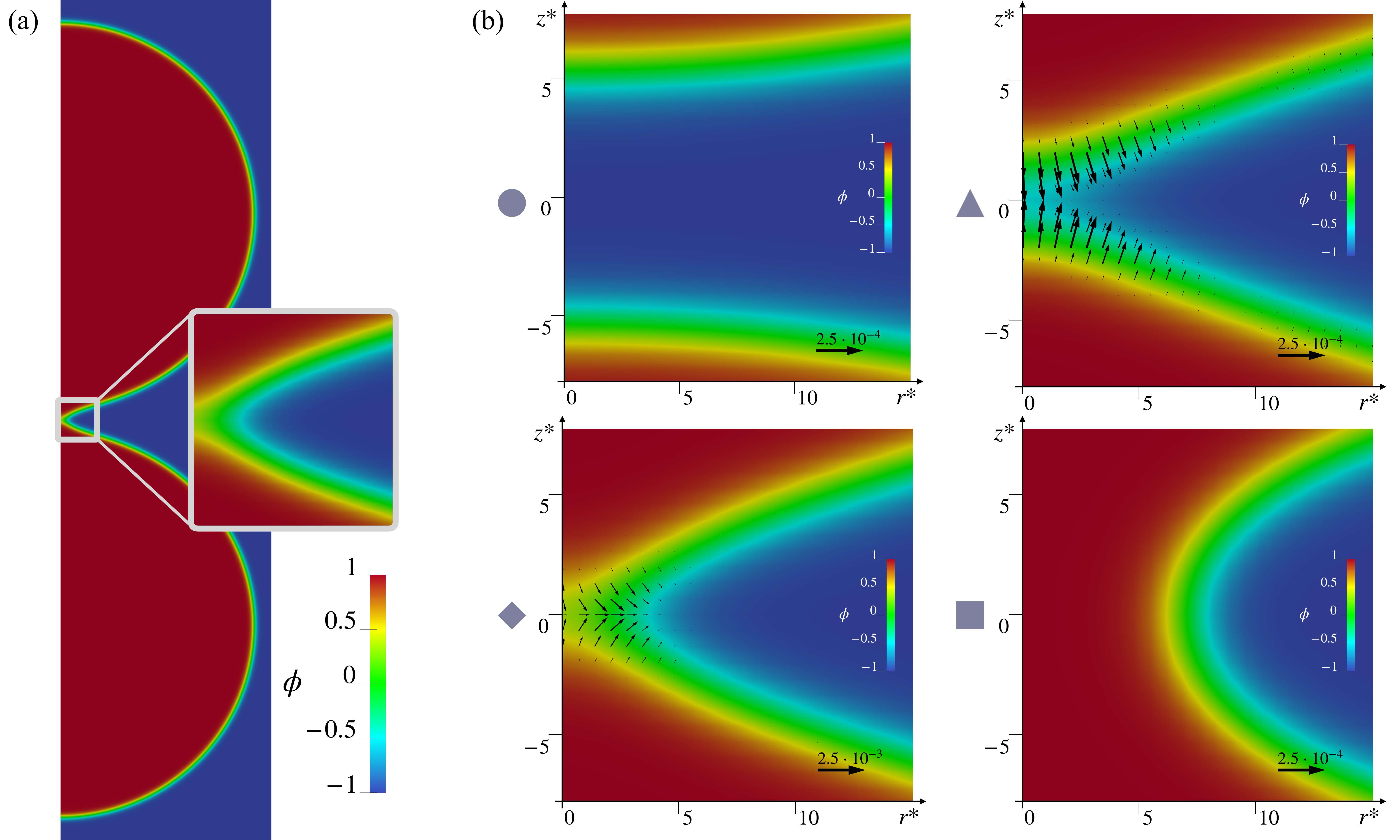
Interestingly, as depicted in Fig. 1,  zooming into the merging region, we find configurations that are reminiscent of those found in experiments and molecular dynamics simulations, i.e. pre-fusion state (circle), stalk (triangle), hemifusion diaphragm (rhombus), and fusion pore (square). The computed differential of forces acting on the hypothetical monolayers initially tends to lyse the bilayer and then to pack back the layers. The differential has two minima exactly in the triangle and rhombus states. The paper also reports the force fields needed to drive the full-scale dynamics of the vesicle.

The approach is expected to pave the way for a series of future works in the field of biomembranes but can also find a much broader scope, e.g. as a way to provide a barrier towards undesired/unphysical fusion processes in surfactant-enriched emulsions. Moreover, the full-scale evolution of a large membrane as described in the paper could be used as a base building block to realize multiscale simulations that can locally take into account the atomistic details in the limited region where lipid rearrangement takes place.