An inhibited laser
Published in Physics
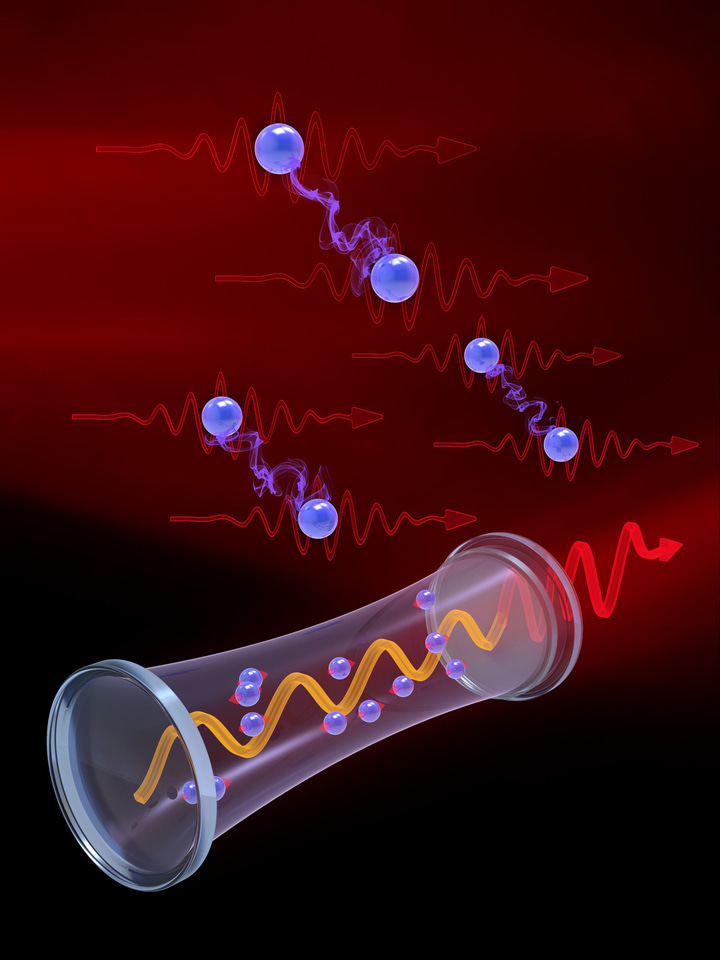
The significantly enhanced spontaneous decay rate of the spin in a resonant circuit, known as the Purcell effect [1], was first reported by Purcell in 1946. Essentially, the resonant cavity, whose cavity-mode frequency resonates with the peak of the emission line for atomic transition, enhances the strength of vacuum fluctuations, which promotes the atomic spontaneous radiation. Conversely, the spontaneous decay rate is suppressed when the cavity is off resonance, which was first proposed by Kleppner in 1981 [2].
In an anti-resonant cavity, where the atomic frequency is exactly at the center of two adjacent cavity resonances, the inhibition of the atomic spontaneous decay rate is the greatest. More strikingly, through coupling with an anti-resonant cavity, the atomic radiative level shift vanished and the spectral linewidth narrowed [3], which is potentially useful for precision measurements. Despite the experimental success of inhibited spontaneous emission, it remains to be explored whether laser oscillations can be realized when the spontaneous emission rate is suppressed to the greatest extent in an anti-resonant cavity, since conventional lasers need cavity resonance as in most laser physics text books. Different from traditional lasers working in the resonant-cavity region, we propose the named inhibited laser operating in the anti-resonant-cavity regime, where the atomic gain line is located exactly between two adjacent cavity resonances. The working principle of the inhibited laser is depicted schematically in Fig. 1. Unlike resonant lasers, the inhibited laser is realized with a round-trip optical path equal to odd multiples of the half wavelength 2L = (2q + 1)λ/2, where q is natural number, and λ the laser wavelength.
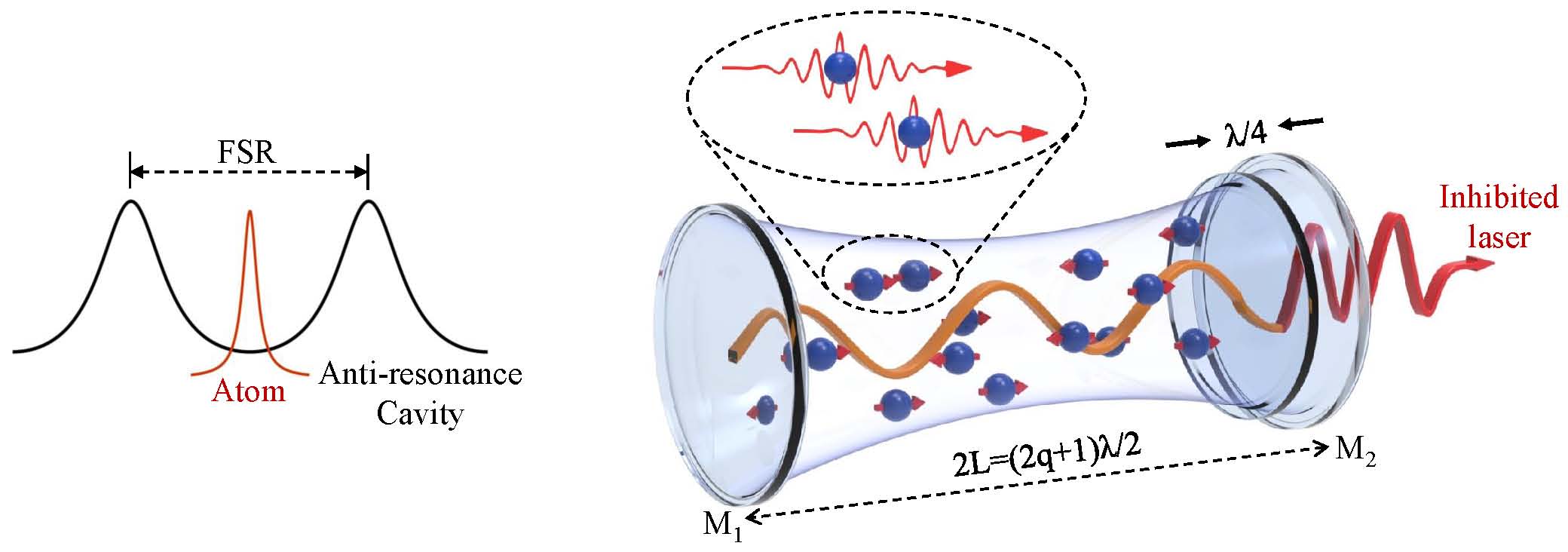
Fig. 1. Working principle of the inhibited laser. The inhibited laser is realized in an anti-resonant cavity, where the atomic gain line is exactly at the center of two adjacent cavity resonances. Generally, the round-trip optical path is exactly equal to an integer multiple of the intracavity wavelengths, and the output mirror is located at M2’. However, an inhibited laser is achieved when the round-trip optical path is equal to an odd multiple of the half wavelength 2L = (2q + 1)λ/2 with the output mirror being located at M2.
Specifically, we experimentally show that the cavity-pulling frequency shift vanishes, while the laser power within an inhibited laser cavity is much lower than outside, just like the eye of a strong tropical cyclone is the location of the storm’s minimum power of typhoon and hurricane. Similar to the eye in hurricanes or typhoons, the convection is almost absent in the circular center. The circling laser waves within the inhibited laser, are strongly inhibited by the reason that the left-traveling wave and the right-traveling are 180 degree anti-phase. Thus, compared with the resonant bad-cavity laser, which exhibit superiority in terms of the high suppression of cavity noise, the influence of the cavity length noise on the quantum frequency of an inhibited laser is further suppressed by an inhibited factor of (2F/π)2 (F is the cavity finesse).
We measured the frequency shift as a function of the cavity-frequency detuning from the atomic transition frequency, as shown in Fig. 2. The experimental results (black triangles) were consistent with the fitted results. Compared with the resonant condition, the suppression of the cavity-pulling effect of inhibited lasers was enhanced from 26 to 53 times.
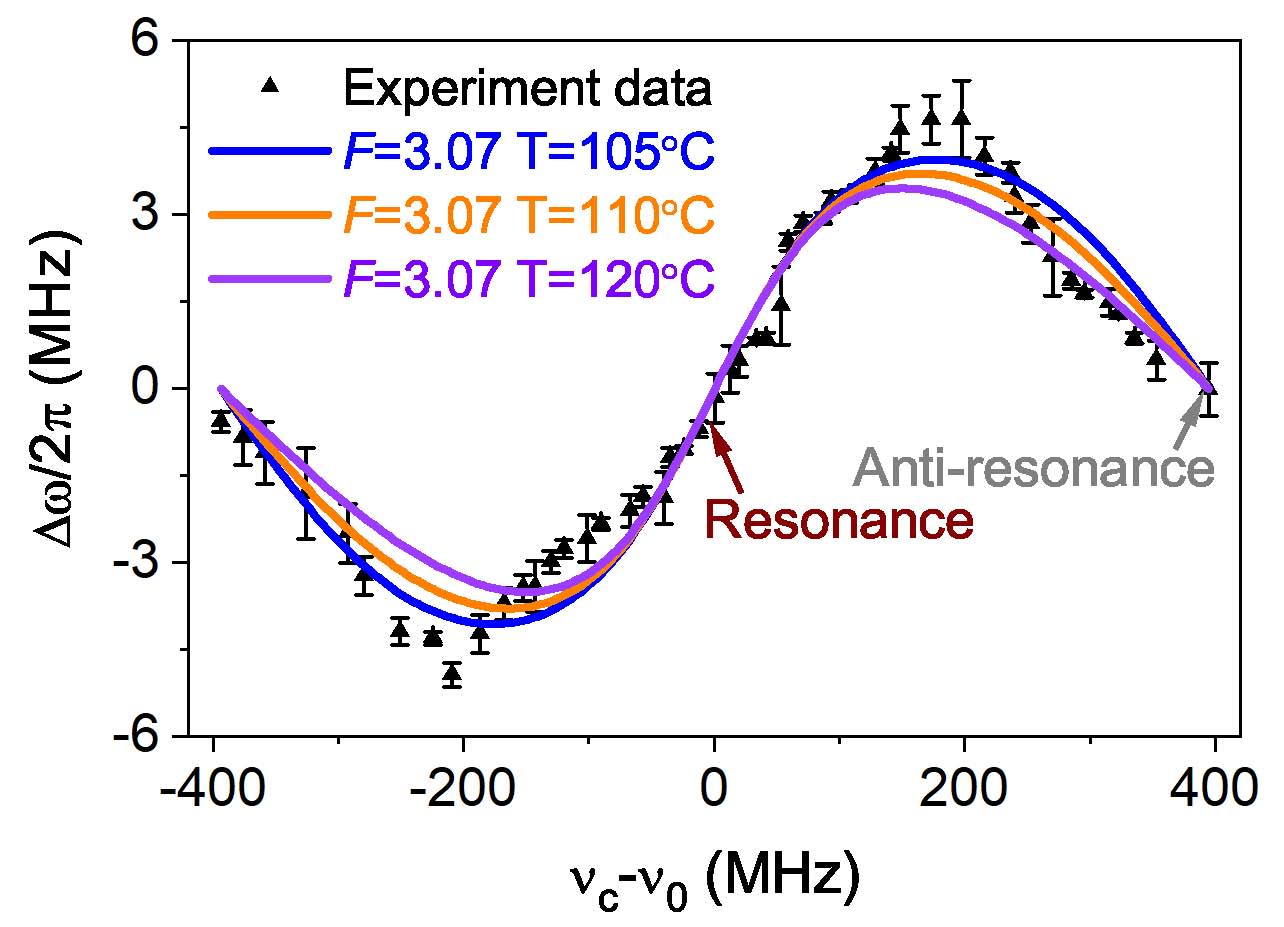
Fig. 2. Frequency shift of the laser oscillation as a function of cavity-frequency detuning from the atomic transition frequency, whose adjustable range was one FSR. The simulated results of frequency shift at different temperatures for F=3.07 are shown as the solid lines, and the black triangles represent the experimental results. Error bars denote standard deviations from three measurements.
Moreover, analogous to the inhibited spontaneous emission, the linewidth of the inhibited laser has the potential to be narrower than that of the traditional resonant laser. In this work, considering the cavity-modification effect, as well as homogeneous and inhomogeneous broadening, we provided the general expression of the laser linewidth. Theoretically, due to the cavity-induced modification following the absorption lineshape with the change of phase shift of cavity, the laser linewidth is expected to be narrowed by a factor of 1/[1+(2F/π)2] for the inhibited laser compared with the resonant one.
Our findings comprise a vivid example of intuitively applying an anti-resonant inhibited laser previously never thought about it to optimize the frequency stability of optical clocks by narrowing laser linewidth and suppressing cavity-pulling effect, which will broaden the horizon of quantum metrology and laser physics.
[1] E. M. Purcell, Spontaneous emission probabilities at radio frequencies, Phys. Rev. 69, 681 (1946).
[2] D. Kleppner, Inhibited spontaneous emission, Phys. Rev. Lett. 47, 233-236 (1981).
[3] D. J. Heinzen, M. S. Feld, Vacuum radiative level shift and spontaneous-emission linewidth of an atom in an optical resonator, Phys. Rev. Lett. 59, 2623-2626 (1987).
Follow the Topic
-
Communications Physics

An open access journal from Nature Portfolio publishing high-quality research, reviews and commentary in all areas of the physical sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Higher-order interaction networks 2024
Publishing Model: Open Access
Deadline: Feb 28, 2026
Physics-Informed Machine Learning
Publishing Model: Hybrid
Deadline: May 31, 2026
Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in