Charting cellular differentiation trajectories with Ricci flow
Published in Cancer, Physics, and Cell & Molecular Biology

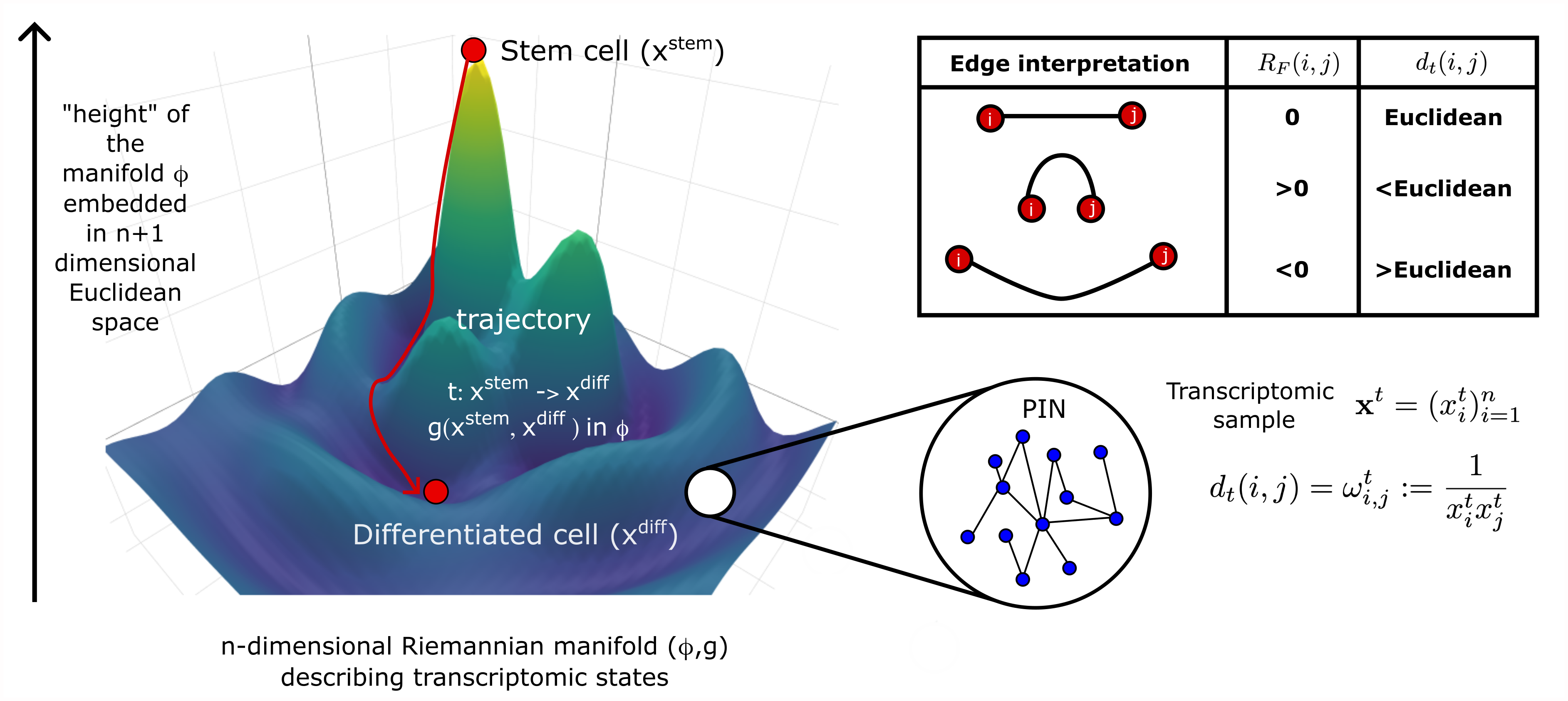
Waddington Landscape
Cellular differentiation is a complex biological process essential for embryonic development as well as the maintenance and repair of adult tissues. Aberrant differentiation underlies a wide spectrum of pathology. This includes malignancy, where cells may fail to differentiate, and become trapped in a more plastic, proliferative state. C. H. Waddington proposed in 1939, a seminal interpretation of the intra-cellular state during differentiation, known as the Waddington Landscape 1. Under this landscape less differentiated cells occupy an elevated position. As cells differentiate they roll down this complex landscape, following a trajectory guided by its hills and valleys, until they reach a stable, differentiated state, an attractor amidst the landscape.
Modern techniques such as transcriptomic and proteomic quantification have illuminated the profound complexity of intracellular states. Moreover, the discovery that we can reprogram cells to earlier phases of differentiation has motivated a recasting of the Waddington Landscape from a metaphorical picture into an interpretable mathematical 2 . Contemporary interpretations of Waddington's Landscape have re-framed cell fate trajectories via the phase space of transcriptomic dynamics. The intra-cellular states of less differentiated cells can also be considered more "promiscuous", characterised by higher entropy in protein-protein interactions, which decreases during differentiation and increases in cancer, providing a quantitative correlate for the "height" in Waddington's landscape 3.
While Waddington's landscape has evolved from a conceptual image to a mathematical construct, the geometric appeal of cell fate transitions persists 4. In this context, geometric approaches to studying cell fate often focus on characterisations of the underlying dynamical system and typically require detailed knowledge of gene regulatory networks relevant to specific cell fate transitions. On a genome-wide scale we lack this deep understanding of intra-cellular interactions and instead rely on sparse graphical representations, known as biological networks, which can be weighted by biological samples to describe relevant dynamics 3 . Despite this limitation, the underlying geometry of biological networks, can be extensively explored through various methodologies, notably network embedding 5.
Geometry and Entropy
Complex systems, especially their geometric descriptions, have been extensively studied for over a century, notably by Einstein's theory of general relativity. This theory elegantly describes the curvature of space-time through the tools of differential geometry, offering a profound understanding of gravity. Concurrently, the dynamic of topological spaces, especially manifolds has been a focal point in differential geometry. Hamilton's seminal work 6 on Ricci flow provided a powerful tool for exploring the topological implications of deforming a manifold's metric according to its Ricci curvature, ultimately leading to Perelman's groundbreaking solution to the Poincaré conjecture.
In recent years, discrete analogues of differential geometric tools have emerged, such as Forman-Ricci curvature (inspired by persistent homology) and Ollivier-Ricci curvature (inspired by optimal transport). These methods have found application in studying biological networks, offering insights into the geometry of cell fate and fostering a rich theoretical literature. Recently, a connection between network entropy and discrete curvature has been proposed 7, drawing inspiration from the theoretical work of Lott and Villani 8, which suggests a link between Ricci curvature and an entropy functional. While network entropy differs theoretically from entropy in metric-measure spaces, research has revealed heightened total Ollivier-Ricci curvature on cancer-weighted networks compared to healthy ones.
These recent results suggest that the geometry of the underlying space of intra-cellular interactions, described by biological networks, may change predictably during their progression. However, comprehensive research on the relationship between network entropy and Ricci curvature, particularly in a biological context, remains limited.
Geometry of cell fate
In the context of cellular differentiation and oncogenesis, we propose a framework based on differential geometry. This framework employs discrete Ricci curvature to elucidate the interplay between entropy and the curvature of cell states, while utilising normalised Ricci flow to forecast dynamic trajectories between gene expression samples connected over time.
Ricci curvature characterises cell states
Firstly, we explore the relationship between our Forman-Ricci curvature construction and network entropy. Through analysis of a simple toy network, we reveal that these two network measures are not always positively correlated. Specifically, in promiscuous signalling environments, such as those found in stem cells, the measures positively correlate. However, in lower entropy regimes, they may exhibit an anti-correlation, suggesting their complementary nature rather than interchangeability. Our analysis of over 6000 single-cell transcriptomes confirms these findings, showing a positive correlation between network entropy and Forman-Ricci curvature in stem cells, but a negative correlation in cancerous and differentiated samples.
Ricci flow predicts cell fate trajectories
Secondly, we investigate two independent transcriptomic time courses detailing multiple time points during cellular differentiation across various tissues. Leveraging our Ricci flow construction, we deduce gene expression trajectories from the initial to the final time point samples, accurately predicting the sequence of intermediate samples without prior knowledge.
These results provide significant evidence on two fronts: theoretically, they bolster the geometric vision for cell fate provided by Waddington; and practically, they offer a novel approach for predicting and inferring cell fate, particularly during oncogenesis.
References:
1 Waddington, C.H.: An Introduction to Modern Genetics. London : George Alien & Unwin. George Alien & Unwin, London (1939)
2 MacArthur, B.D., Maayan, A., Lemischka, I.R.: Systems biology of stem cell fate and cellular reprogramming. Nature reviews. Molecular cell biology 10, 672–681 (2009)
3 Banerji, C.R.S., Miranda-Saavedra, D., Severini, S., Widschwendter, M., Enver, T., Zhou, J.X., Teschendorff, A.E.: Cellular network entropy as the energy potential in waddington's differentiation landscape. Scientific Reports 3(1), 3039 (2013)
4 MacArthur, B.D.: The geometry of cell fate. Cell Systems 13, 1–3 (2022)
5 Baptista, A., Sanchez-Garcıa, R.J., Baudot, A., Bianconi, G.: Zoo guide to network embedding. Journal of Physics: Complexity 4(4), 042001 (2023)
6 S., H.R.: The ricci flow on surfaces. Contemporary Mathematics (71), 237–262 (1988)
7 Sandhu, R., Georgiou, T., Reznik, E., Zhu, L., Kolesov, I., Senbabaoglu, Y., Tannenbaum, A.: Graph curvature for differentiating cancer networks. Scientific reports 5(1), 1–13 (2015)
8 Lott, J., Villani, C.: Ricci curvature for metric-measure spaces via optimal transport. Annals of Mathematics 169(3), 903–991 (2009)
Follow the Topic
-
Nature Communications

An open access, multidisciplinary journal dedicated to publishing high-quality research in all areas of the biological, health, physical, chemical and Earth sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Women's Health
Publishing Model: Hybrid
Deadline: Ongoing
Advances in neurodegenerative diseases
Publishing Model: Hybrid
Deadline: Mar 24, 2026

Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in