Ethylene carbonate, for instance, is a solid at room temperature, but it becomes functional in electrolyte solutions when combined with other components enabling the electrolyte solution to be liquid over the temperature range of operation.  The simplest theory for understanding mixtures is linear mixing.  The deviation from linear mixing is known as the excess property, e.g. excess molar enthalpy.  Mixtures obey an interesting property of permutation invariance, i.e. the answer should remain the same under a swap of ordering.  The simplest function that remains invariant is the product of the mole fractions.  Let’s discuss this with the example case of the excess molar enthalpy of a mixture of propylene carbonate and ethyl phenyl ether.  As you can see below, this simple function captures most of the essence. 

However, there is asymmetry in the mixing behavior which requires moving beyond this.  Otto Redlich and A. T. Kister, then at Shell,  introduced a polynomial expansion with the variable of expansion being the difference of the two components, which retains permutation invariance.  With an expansion for 2 additional terms, we get a nearly perfect fit for the data at hand.  The higher order terms describe the subtle nature of interactions between these two mixtures, this subtlety is what determines their functionality in a wide variety of applications.

Making Mixture Laws Differentiable

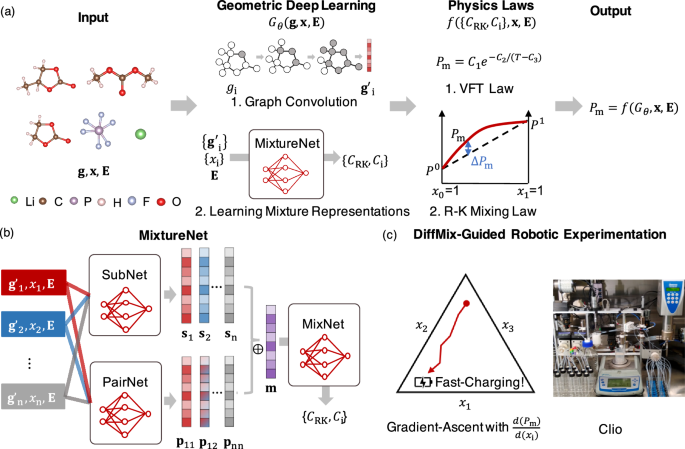
The problem of developing a mixture law now boils down to simply learning the coefficients of these mixture physics laws.  The key challenge lies in linking the identity of the molecules to these coefficients.  There has been extraordinary progress in the last decade representing molecules using graphs. My PhD student, Shang Zhu, had the deep insight of directly learning the coefficients from the molecular identity as a learning problem.  In order to realize this idea, we need to code up the mixture physics laws written using differentiable programming.  In early 2021, together with Bharath Ramsundar, we made the observation that differentiable physics opens up a totally new paradigm for physical modeling.  Now, it was Shang’s turn to take the differentiable physics idea to mixture physics with DiffMix. Shang proceeded to curate a dataset of excess thermodynamic quantities of molar enthalpy, molar volume and the core idea worked.  The next step is to take on a more ambitious task!  

Where DiffMix Meets Electrolytes

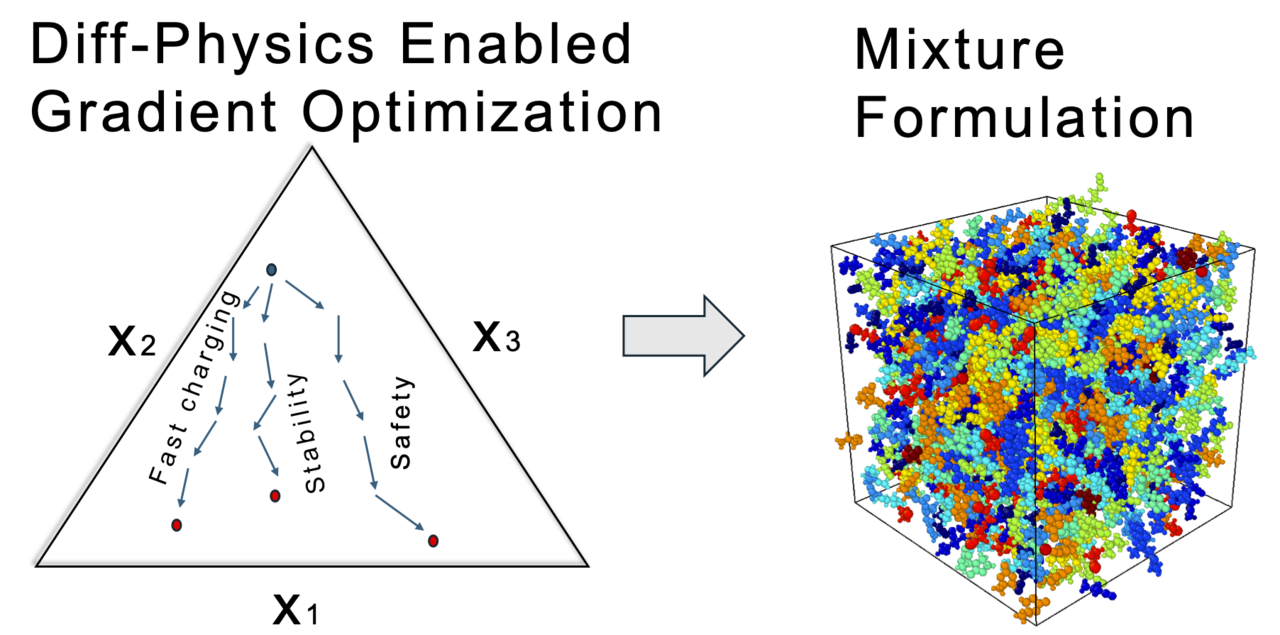
Designing electrolyte mixtures for batteries is such an ambitious task.  Shang decided to tackle the problem of designing an electrolyte mixture that has high ionic conductivity, an important attribute to realize fast discharging critical for electric aviation and fast charging, critical in automotive applications.  At this time, my group had a long-standing collaboration with Dr. Kevin Gering, who had developed the Advanced-Electrolyte-Model (AEM), an advanced simulation engine that could provide the dataset needed to realize this task.  Shang curated a dataset of over 20,000 data points for ternary-solvent and single-salt electrolytes with varying chemical identities.  Now, we were off to the races.

Bridging Simulation to The Real World, with a Robot

We trained a model for ionic conductivity, but we needed a way to test how well does DiffMix do in designing an electrolyte formulation? My group had built a robotic test stand, called Clio which can test electrolyte mixtures.  Shang enticed Hongyi and Adarsh to test and validate an optimization trajectory in a ternary chemical space.  This feels especially appropriate, given that the  ARPA-E DIFFERENTIATE program funded the project, and we utilized differentiation in chemical space for gradient-based optimization.  Now comes the nerve-racking validation experiment and the optimization trajectory measured from our robotic electrolyte setup, Clio, matched the predictions of the model.  A tour-de-force!

The work is an organic fusion of so many disciplines that rarely come together - differentiable programming, chemical physics, geometric deep learning and autonomous experimentation.  That’s the level of interdisciplinary innovation needed to realize new functional mixtures for energy storage and to shorten the timescale for lab-scale materials innovation to reach commercialization.