Semiconductor devices have been the dominant technology for our computing systems since the dawn of the information age. The performance and efficiency of this technology is unlikely to be matched by any other, any time soon. And yet, the impetus to study alternative information storage and data processing methodologies is clear. Eventually, some of these could displace semiconductor transistors as general-purpose computing devices. In specific contexts, alternative technologies could have compelling advantages that are immediately apparent. Such contexts include biological compatibility as well as computing in challenging environmental conditions. Making devices that work seamlessly with our bodies and in our environment is a grand challenge for computing engineering. 

An exciting direction of research in this vein is molecular computing, a paradigm that relies on chemical reactions rather than traditional silicon chips. This approach has the potential to be considerably more parallelizable and energy efficient than existing silicon-based computers. Our work demonstrates a new paradigm in chemical-based computing, where we utilize a pH-based system to encode the data and acid-base reactions for universal computations, orchestrated by a robotic liquid handler. The chemical basis for our system is the neutralization reaction of acids and bases. 

In this work, we recognize and leverage the fact that the neutralization reaction between acids and bases is analogous to the majority function in Boolean logic because it leaves behind only the more abundant species. The majority function, when paired with the inversion operation, forms a functionally complete set. This means that these two operations alone can model any Boolean logic function.

However, the inversion operator is challenging to realize in chemical computation; inversion would require a conditional bistable chemical network that can be toggled without knowledge of the current state. To the best of our knowledge, no simple reaction would change an acid to a base and a base to an acid. Thus, we overcome this challenge by using dual-rail encoding to represent data values as complementary pairs. In our pH-based dual-rail encoding, the data is encoded as complementary pairs of (Acid, Base) or (Base, Acid) where each rail has a pH of 14.0 - pH of the other rail. Thus, using this encoding, we can readily realize inversion operations by simply exchanging the chemical rails during our computations. 

In our work recently published in Nature Communications, we developed a unique computational system that we used to model digital circuits and image classification networks based on acid-base chemistry. Figure 1 shows the overview of our system.

We first created a binary data encoding system using a pH-based dual-rail representation. This system uses pairs of complementary solutions; the pair (Acid, Base) represents the value “1” or “TRUE,” while the pair (Base, Acid) represents the value “-1” or “FALSE.” Additionally, we extended this encoding to represent more discrete values by controlling the concentration of the encoded values. A more concentrated solution indicates a more positive or negative value than a diluted solution.

Next, we used this pH-based encoding to model digital circuits. As mentioned earlier, the acid-base neutralization reaction is analogous to the majority function in Boolean logic, which allows us to model all primitive logic gates (AND, OR, INV, NAND, and NOR), as shown in Figure 2. 

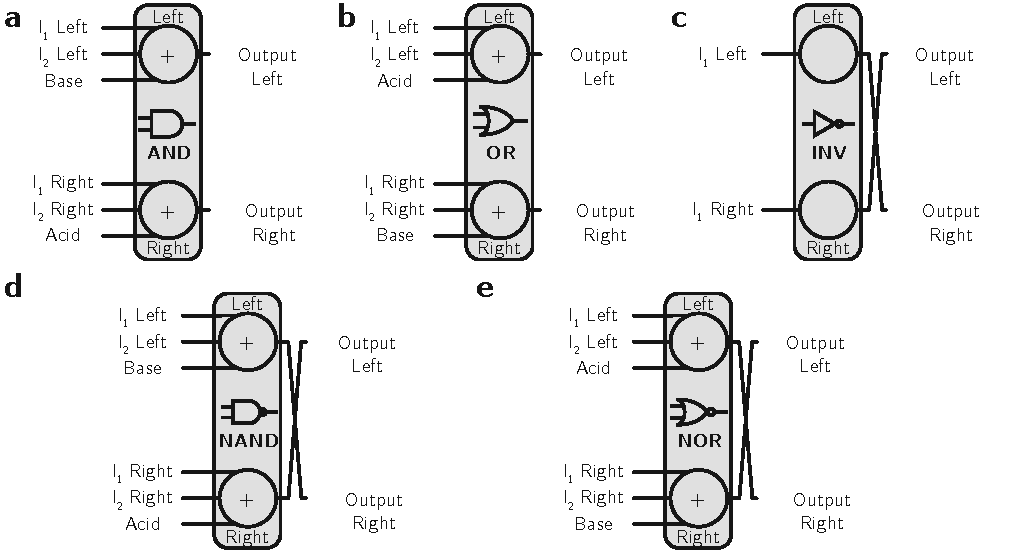
All the building blocks should have an odd number of inputs to avoid neutral pH outputs; hence, a third input is added as a constant bias to construct two-input logic gates.

Lastly, we used acid-base reactions to model a neural network for image classification. Each pixel of a binary or grayscale image was encoded using our pH-based dual-rail system. We then trained a network in-silico using binary weights  (+1 or -1). The classification of an image is represented as a set of neutralization reactions carried out on each pixel. The reactions are executed for each neuron to calculate the probability for the class associated with the neuron. The pixels associated with a negative weight have their dual-rail flipped before mixing to represent multiplication by -1. In the end, each neuron is represented by an acid-base pair whose value could be easily measured using a simple pH indicator. A pair of (Base, Acid) indicates a neuron output of -1, while a pair of (Acid, Base) indicates a neuron output of +1. As an example, Figure 3 demonstrates how this system can classifies the digit “one” using acid-base chemistry. 

In summary, in this study, we demonstrated the potential of pH encoding and acid-base reactions as a basis for complex computation. We implemented the previous models with the help of an acoustic liquid handler which functions similarly to wires in an electronic circuit by transporting our stored chemical information and conducting computation through mixing. One of our approach’s key innovations is using a dual-rail encoding method that leverages the natural complementarity of acids and bases. This method enables our system to support the negation operation, which is crucial for achieving universal computation. Additionally, we took advantage of the fact that the pH of a strong acid/base system is primarily determined by the species that is more concentrated to implement the majority function in chemistry. Furthermore, the reactions enable rapid computation due to the speed of strong acid/base reactions without the need for intricate equipment to execute the operations. At the same time, the readout is done using cheap pH indicators.

These new encodings based upon acid-base chemistry can open up new possibilities for computing with molecular data storage systems. For example, by interacting with pH-dependent protection/deprotection groups that could be incorporated into DNA or small molecule information storage systems. We also proposed a solution to the dilution problem by manually replacing intermediate results with fresh non-diluted stocks of acids or bases. However, this step can be automated by combining with other existing concepts, such as using pH-sensitive hydrogel valves to build a restoration mechanism to maintain the computation across a longer chain of reactions. This research presents a new paradigm for computing using pH encoding and acid-base chemistry that could have a wide range of applications in the field of information technology.