Dirac synchronization is rhythmic and explosive
Published in Physics
Topology is recognized to play a fundamental role in theoretical physics, statistical mechanics and condensed matter, however the investigation of how topology can affect synchronization is only at its infancy [1].
Synchronization is a fundamental collective phenomenon describing a large variety of natural systems ranging from neuronal and brain dynamics to coherent fireflies flashing in tropical forests and to applications also in quantum condensed matter.
The Kuramoto model [2] originally formulated by Kuramoto in 1975 is capturing the synchronization of many non-identical oscillators. In the original Kuramoto model these oscillators are placed on the nodes of networks, while the edges describe the coupling between oscillators placed on linked nodes. When the coupling constant is above the synchronization threshold a finite fraction of oscillators starts to oscillate at the same frequency, leading to the widely celebrated second order synchronization phase transition of the Kuramoto model.
Recently, growing attention has been directed to topological signals, i.e. dynamical variables not only defined on the nodes of the network but also on its links [3]. In neuronal networks, topological signals defined on the edges of the network, also called edge signals, can be used to represent synaptic signals mediated by the current of neurotransmitters while in brain networks edge signals can represent instantaneous functional activations of links.
Actually, topological signals can be defined also on higher dimensional units as triangles and tetrahedra if the complex system under study can be captured by a higher-order network in which the interactions can occur between two or more nodes. Previous results [1] have shown that topological signals of a given dimension such as edge signals can undergo a synchronization phase transition. However how to couple topological signals of different dimension such as node signals (e.g. neuronal signals) and edge signals (e.g. synaptic signals) remains mostly unexplored so far.
In [4] we show that topological signals of nodes and edges can undergo a collective phase transition when they are locally coupled by the Dirac operator. The Dirac operator [5] is an operator inspired by quantum mechanics, but fully grounded in discrete topology. In particular its defining property is that its square is given by the Laplacian operator, therefore it can be interpreted as the “square root” of the Laplacian. The Dirac operator couples node signals to signals of nearby edges and viceversa couples edge signals to signals of nearby nodes. In [4] the Dirac operator is used for the first time to study synchronization. The resulting collective dynamical processes of coupled topological signals is called Dirac synchronization. Dirac synchronization displays an emergent rhythmic phase and an explosive transition and can elucidate how topology can be a driver element to establish brain rhythms.
Results
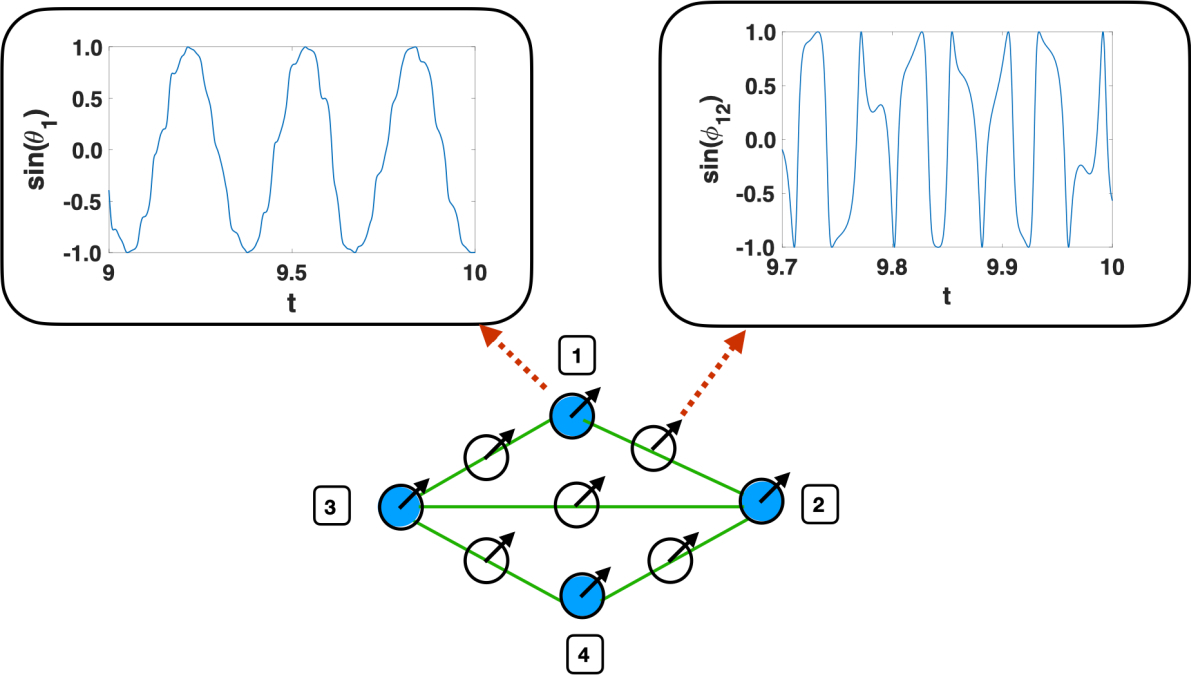
Dirac synchronization is a collective phenomenon involving non-identical oscillators placed on each node and each edge of the network. The coupling between oscillators of nodes and edges is enforced by considering a Kuramoto-like dynamics where the oscillators placed on the nodes have a phase-lag depending on the oscillators of nearby edges and viceversa the oscillators placed on the edges are affected by a phase-lag depending on the dynamical state of nearby nodes (see Fig.1).
Fig. 1 | Schematic representation of node and edge signals coupled by Dirac synchronization. In Dirac synchronization non-identical oscillators are placed on each node and each edge of the network. Oscillators on the nodes are coupled to oscillators of nearby edges and oscillators on the edges are coupled to oscillators of nearby nodes.
Dirac synchronization admits two complex order parameters X𝛼 and X𝛽 each depending on both nodes and edge signals demonstrating the very intertwined dynamics of the two types of topological signals.
Dirac synchronization is rhythmic. Indeed, the coherent synchronized state is characterized by emergent oscillations of one of the complex order parameters. These oscillations depend on the network structure rather than the intrinsic frequencies of the oscillators of nodes and edges. Indeed, the order parameter X𝛼 oscillates at very slow frequency also in the rotating frame determined by the intrinsic frequencies of the nodes' and edges' oscillators (see Fig.2). Therefore, Dirac synchronization demonstrates that a topological and local coupling of node and edge signals enforced by the Dirac operator can lead to an emergent rhythmic synchronized phase.
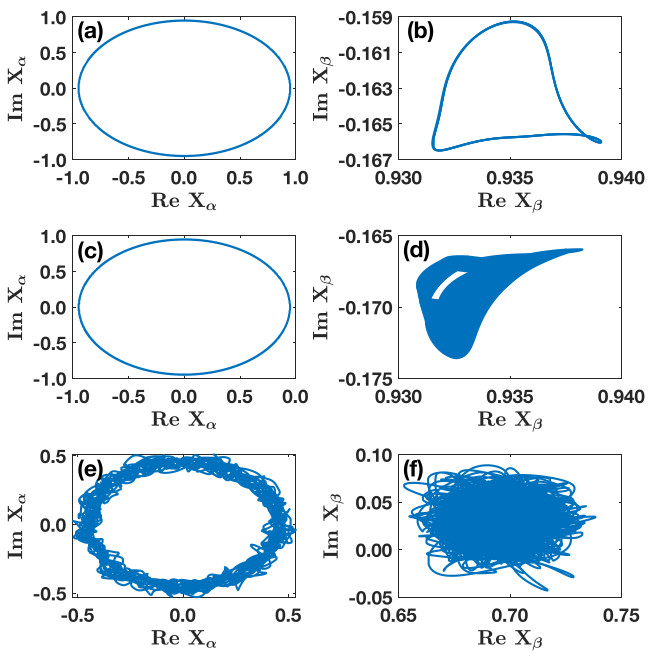
Fig. 2 | Dirac synchronization is rhythmic. The phase potraits of the complex order parameters X𝛼 and X𝛽 of Dirac synchronization are revealing the rhythmic nature of the synchronized phase also in the rotating frame of the intrinsic frequencies. In particular X𝛼 is shown to oscillate at almost constant frequency in the imaginary plane for larger values of the coupling constant (panel a) while for increasingly smaller coupling constants (panels c and e) approaching the desynchronization phase transition additional fast frequency oscillations set in (panel e).
Dirac synchronization is explosive. If we focus on the absolute value of the complex order parameters R𝛼 =| X𝛼 | and R𝛽 =| X𝛽 | as a function of the coupling strength 𝜎, we observe a phase diagram radically different from the phase diagram of the ordinary Kuramoto model (see Fig.3). The ordinary Kuramoto model is characterized by a second order phase transition observed at the bifurcation point when the collective synchronized phase emerges. At this synchronization threshold the incoherent state becomes also unstable, therefore the forward and backward synchronization transition coincide. The phase diagram of Dirac synchronization, determined by the two order parameter R𝛼 and R𝛽, is significantly different. The forward and the backward transitions do no longer coincide, and the forward transition is now discontinuous and explosive indicating that Dirac synchronization occurs abruptly if the coupling constant is increased starting from zero. Interestingly the discontinuity of the forward synchronization transition is solely due to the coupling of nodes and edge signals occurring in the Dirac synchronization. In fact this phenomenon is not observed if node and edge signals are not coupled to each other.
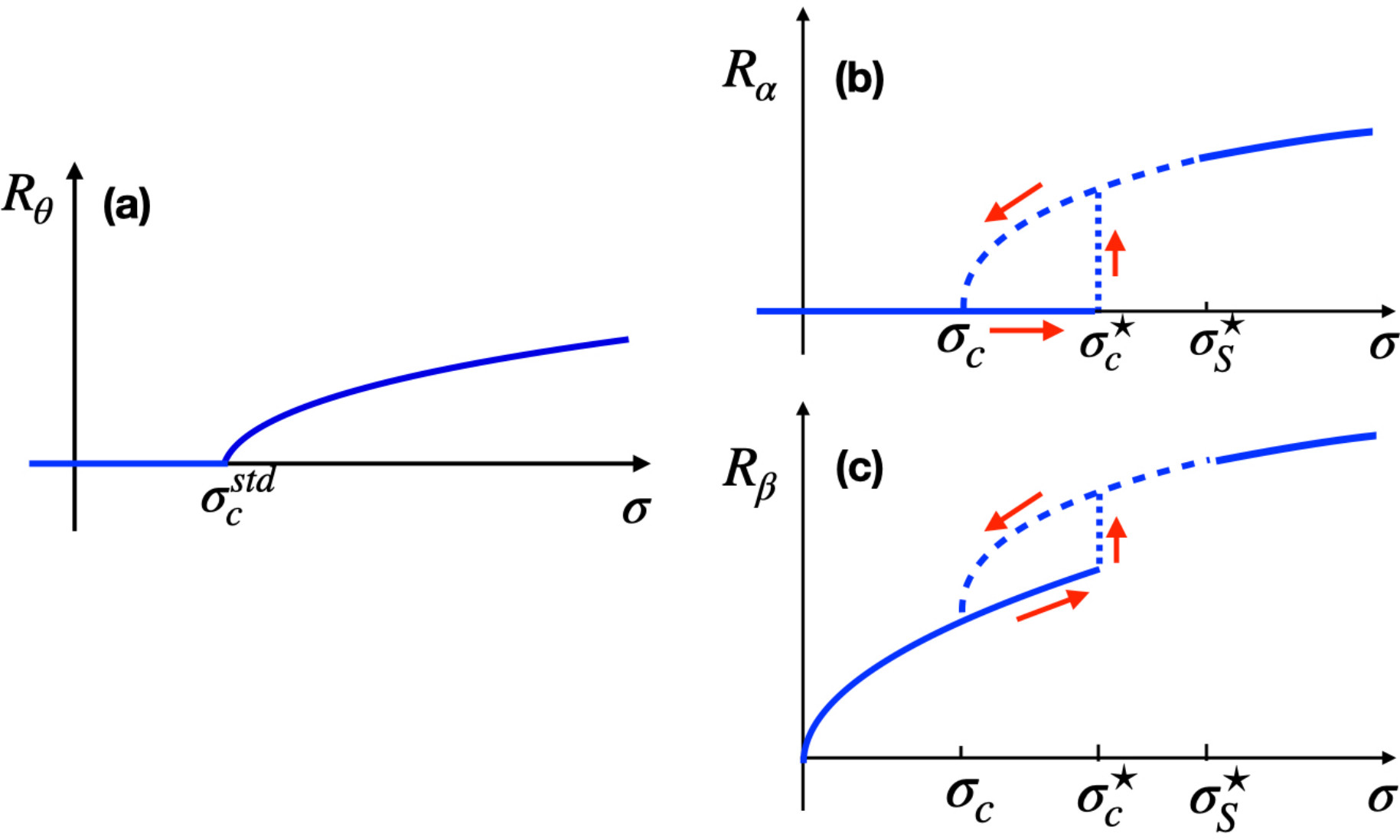
Fig. 3 |Schematic phase diagram of ordinary Kuramoto model and of Dirac synchronization. The phase diagram of the ordinary Kuramoto model (panel a) is a second order phase transition with the forward and the backward transition coinciding. The phase diagram for Dirac synchronization (panels b and c) instead reveals the discontinuous nature of the forward transition. The long dashed line indicates the rhythmic phase which becomes the only coherent phase in the infinite network limit.
This schematic phase diagram is confirmed by the theoretical derivation of the phase diagram of Dirac synchronization on a fully connected network which is in very good agreement with extensive numerical simulations (Fig. 4).
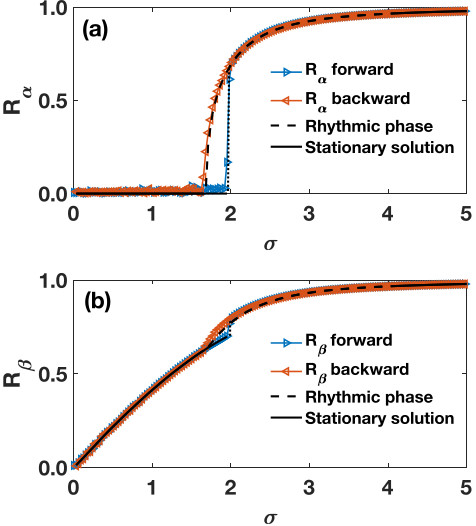
Fig. 4 | The phase diagram of Dirac synchronization. The phase diagram of Dirac synchronization on a fully connected network shows very good agreement between the theoretical predictions (black solid and dashed lines) and the numerical results (red and blue symbols).
In conclusion Dirac synchronization uses topology and in particular the Dirac operator to describe the emergence of a rhythmic phase at a discontinuous transition. These results open new perspectives in the study of collective phenomena of topological signals and might explain how topology can provide mechanisms for the emergence of brain rhythms.
References
[1] Millán, A.P., Torres, J.J. and Bianconi, G., 2020. Explosive higher-order Kuramoto dynamics on simplicial complexes. Physical Review Letters, 124(21), p.218301.
[2] Kuramoto, Y., 1975. Self-entrainment of a population of coupled non-linear oscillators. In International symposium on mathematical problems in theoretical physics (pp. 420-422). Springer, Berlin, Heidelberg.
[3] Battiston, F., Amico, E., Barrat, A., Bianconi, G., Ferraz de Arruda, G., Franceschiello, B., Iacopini, I., Kéfi, S., Latora, V., Moreno, Y. and Murray, M.M., 2021. The physics of higher-order interactions in complex systems. Nature Physics, 17(10), pp.1093-1098.
[4] Bianconi, G., 2021. The topological Dirac equation of networks and simplicial complexes. Journal of Physics: Complexity, 2(3), p.035022.
[5] Calmon, L., Restrepo, J.G., Torres, J.J. and Bianconi, G., 2022. Dirac synchronization is rhymthic and explosive. Communications Physics 5, 253 | https://doi.org/10.1038/s42005-022-01024-
Follow the Topic
-
Communications Physics

An open access journal from Nature Portfolio publishing high-quality research, reviews and commentary in all areas of the physical sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Higher-order interaction networks 2024
Publishing Model: Open Access
Deadline: Feb 28, 2026
Physics-Informed Machine Learning
Publishing Model: Hybrid
Deadline: May 31, 2026

Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in