Higher-order triadic interactions reveal the dynamical nature of percolation
Published in Physics
Connectivity it is a necessary requirement for emergent collective phenomena in complex interacting systems. Percolation theory, mathematically characterizing the network connectivity is therefore one of the most successful and pervasive approach to characterize networks and their response to perturbations. However standard percolation has the limitation that cannot account for time-varying connectivity such as the one observed in climate and brain networks.
The typical problems that standard percolation addresses is how the size of the giant component, the largest extensive connected component of the network, is affected after a random or targeted damage, or alternatively, how a set of random failures might trigger an avalanche and suddenly dismantle the network.
However, connectivity in climate or brain networks can have strong temporal fluctuations and the size of the giant component can vary non-monotonically in time. Think for instance at videos representing the resting activity of the brain. In this case the connectivity of the brain networks has strong spatio-temporal fluctuations in which the fraction of nodes in the largest connected component changes in time in a seemingly unpredictable way. Similarly the giant component of climate networks display a highly complex dynamics.
In [1] we show that higher-order interactions and specifically triadic interactions can drastically modify our understanding of percolation and turn percolation into a fully-fledged dynamical process that can account for large fluctuations of the set of nodes involved in the giant component and of their number (the size of the giant component).
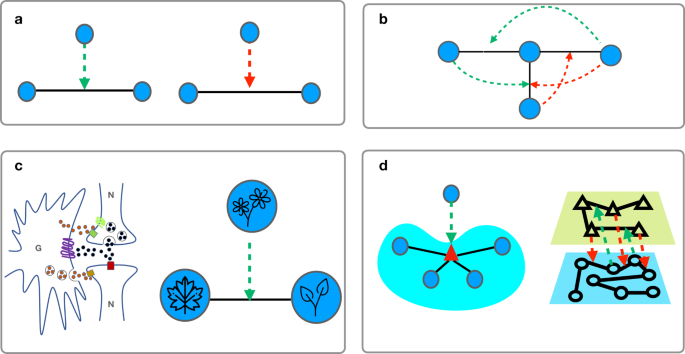
Triadic interactions are an ubiquitous example of higher-order interactions in which one node affects the interactions between other two nodes, which have been widely studied in the context of ecosystems, and neuroscience [2,3]. However these interactions have not been yet extensively studied for the investigation of large scale properties of networks.
Here we show that signed triadic interactions change the nature of the percolation transition. In the standard percolation problem percolation displays a second order, continuous phase transition. This phase transition is drastically changed when signed triadic interactions are taken into account as these interactions can induce blinking and chaos in the connectivity of the network. As a result, the order parameter undergoes a route to chaos. Our theory is validated with extensive simulations on synthetic and real-world networks. These results radically change our understanding of percolation and can be used to shed light on real systems in which the functional connectivity of the network is strongly dependent on time as in neuronal and brain networks and in climate [4].
Results
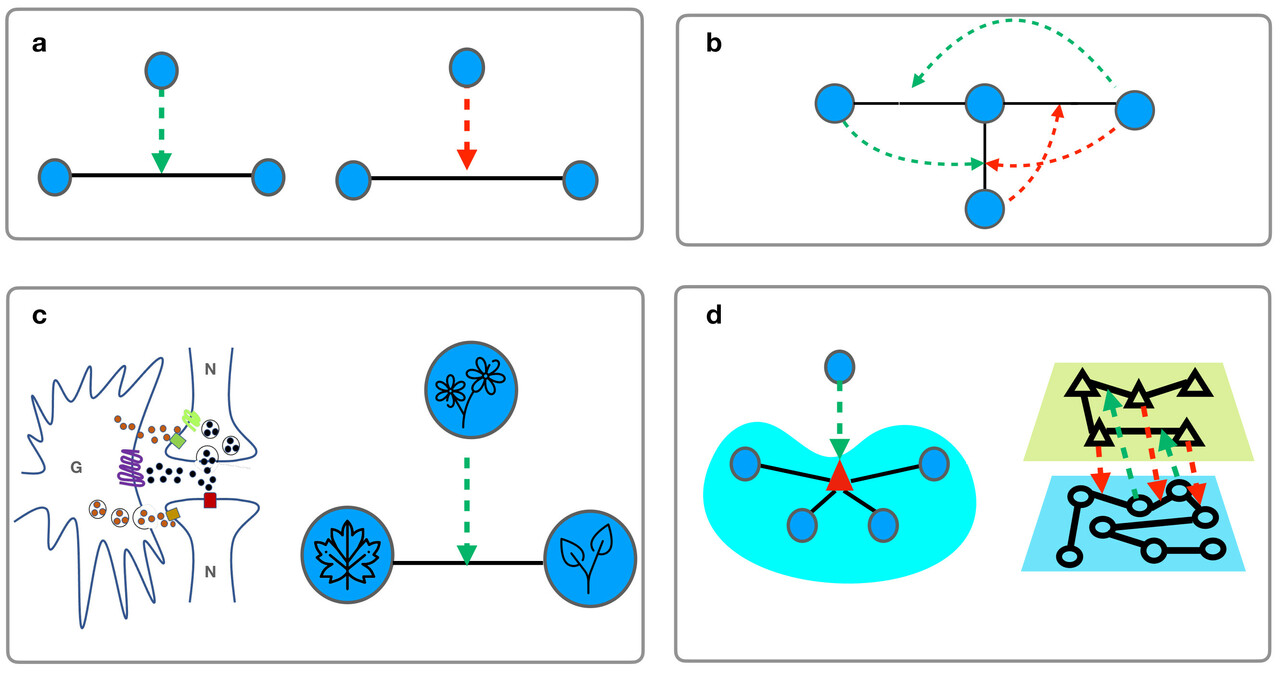
In [1] we propose triadic percolation, a model to capture the dynamical nature of percolation in presence of signed triadic interactions. Triadic interactions (see Fig 1) are higher-order interactions occurring when a node affects/regulates the interaction between other two nodes. These triadic interactions occur ubiquitously in complex systems. For instance, in neuronal networks a glia can affect the synaptic interactions between two neurons, or in ecosystems one species can affect the interaction between other two species. Interestingly triadic interactions can be signed: for instance, a species can enhance or inhibit the interactions between other two species. Triadic interactions can be extended to treat regulations of hypergraphs and regulation occurring between the layers of a multilayer network structure.
Despite the significant interest in triadic interactions [2,3] in ecosystems and neuroscience literature the role of triadic interactions in modulating the large scale properties of higher-order networks has been so far mostly unexplored.
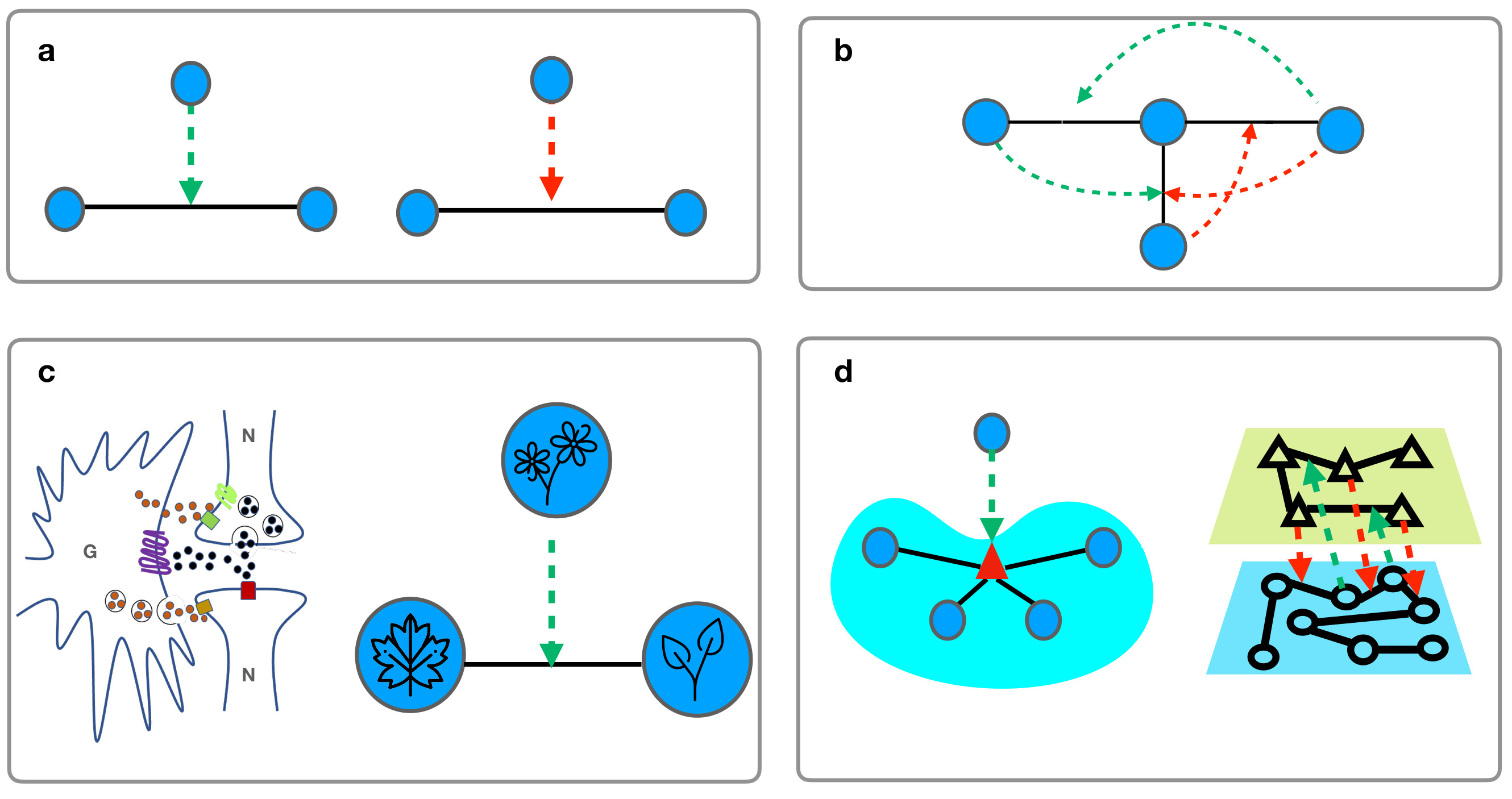
Fig. 1 | Schematic representation triadic interactions. Triadic interactions occur when a node regulates the interactions between two other nodes. Triadic interactions can be signed (panel a) forming a network with triadic interactions (panel b). Panel (c) provides a schematic representation of triadic interactions in complex systems. Panel (d) present the generalization of triadic interactions to hypegraphs and multiplex networks.
Triadic percolation assumes that triadic interactions regulate the activity of the links that are switched on and off depending on the state of their regulatory nodes. In its simplest form, triadic percolation is a two step process that is iterated in time: first the nodes in the giant component are activated, secondly the links are up or down regulated according to the state of the activity of their regulator nodes and to a suitable Boolean rule.
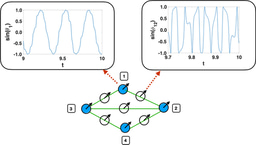
When this two steps process is iterated in time we can observe the network “blinking”, i.e. a dynamical state in which the giant component oscillates between two or more states periodically in time with different part of the network switching on and off in time (see Fig.2). Moreover the order parameter of triadic percolation indicating the fraction of nodes in the giant component undergoes a route to chaos (proved to be in the universality class of the logistic map). Therefore triadic percolation can be found in a chaotic state in which the time series indicating the fraction of nodes in giant component is chaotic (see Fig. 2).

Fig. 2 |Time-varying size of the giant component in percolation. The theory of triadic percolation (panels a-c) predicts a time-varying size of the giant component (panel d-f). The size of the giant component undergoes periodic oscillations (blinking, panels b,e) or a chaotic dynamics (panels c,f) for some parameters while for others can describe a stationary state of the giant component (panels a,d).
In our work we provide a complete theory for triadic percolation which combines the theory of percolation with the theory of dynamical processes. In particular we show that on a random graph the phase diagram of triadic percolation is drastically different from the phase diagram of standard percolation in absence of triadic interactions. While standard percolation displays an ordinary second order phase transition, the phase diagram of triadic percolation is an orbit diagram describing the route to chaos of the percolation order parameter.
Our theory is able to predict the phase diagram observed numerically with a very high level of precision (see Fig. 3) although the full triadic percolation is captured only by three equations also for networks having several thousand of degrees of freedom (triadic interactions).
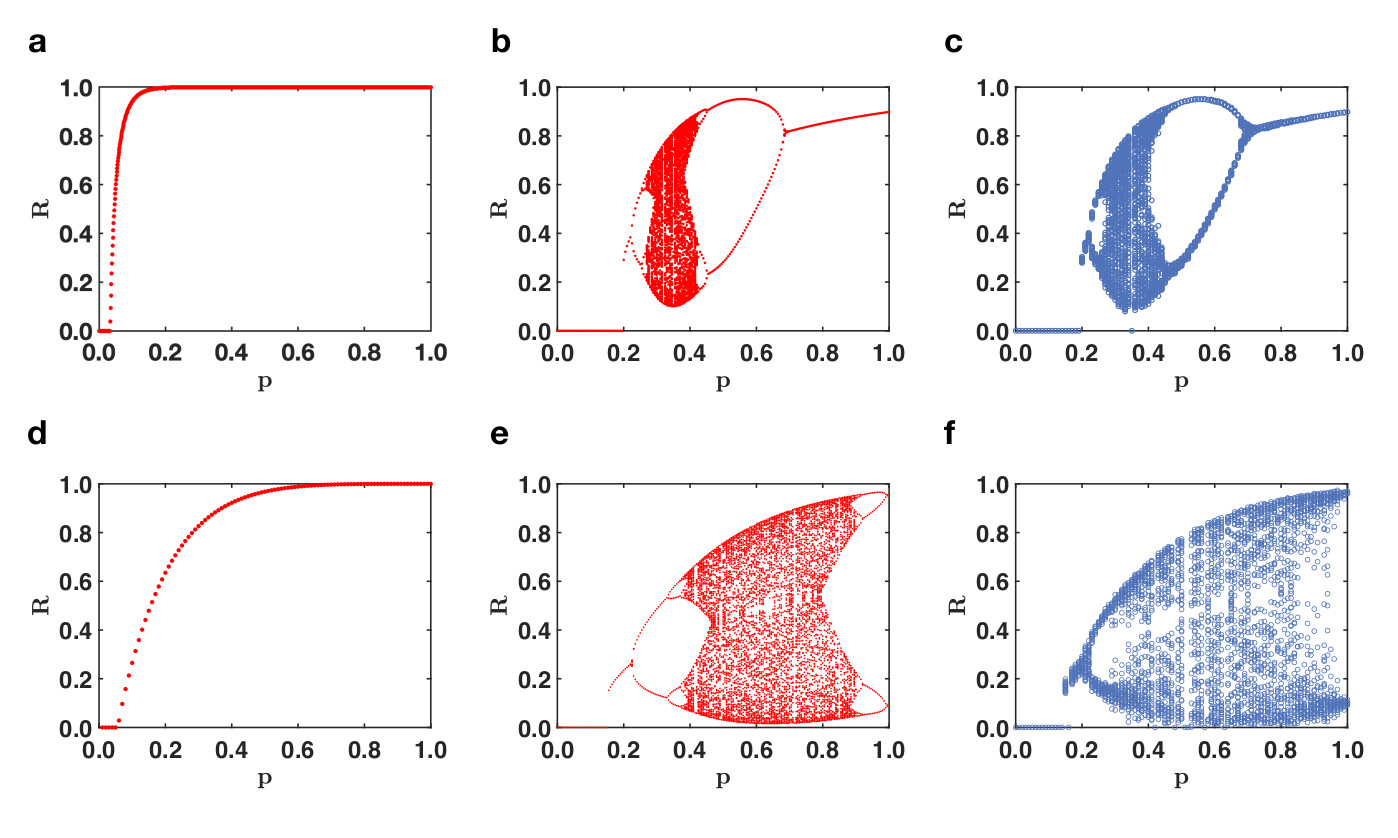
Fig. 3 | The phase diagram of triadic percolation is an orbit diagram. The phase diagram of standard percolation (panel a,d) is drastically changed for triadic percolations (b,c,e,f) on both Poisson and scale-free networks. Panel (b,e) refer to theoretical predictions panels (e,f) refers to MonteCarlo simulations of triadic percolation.
Triadic percolation is also tested on the real network topologies of the mouse connectome and the biogrid network. This result reveals that also if the underlying network topology is not a random graph, triadic percolation is shown to induce both blinking and chaos in the connectivity of the network (see Fig. 4).
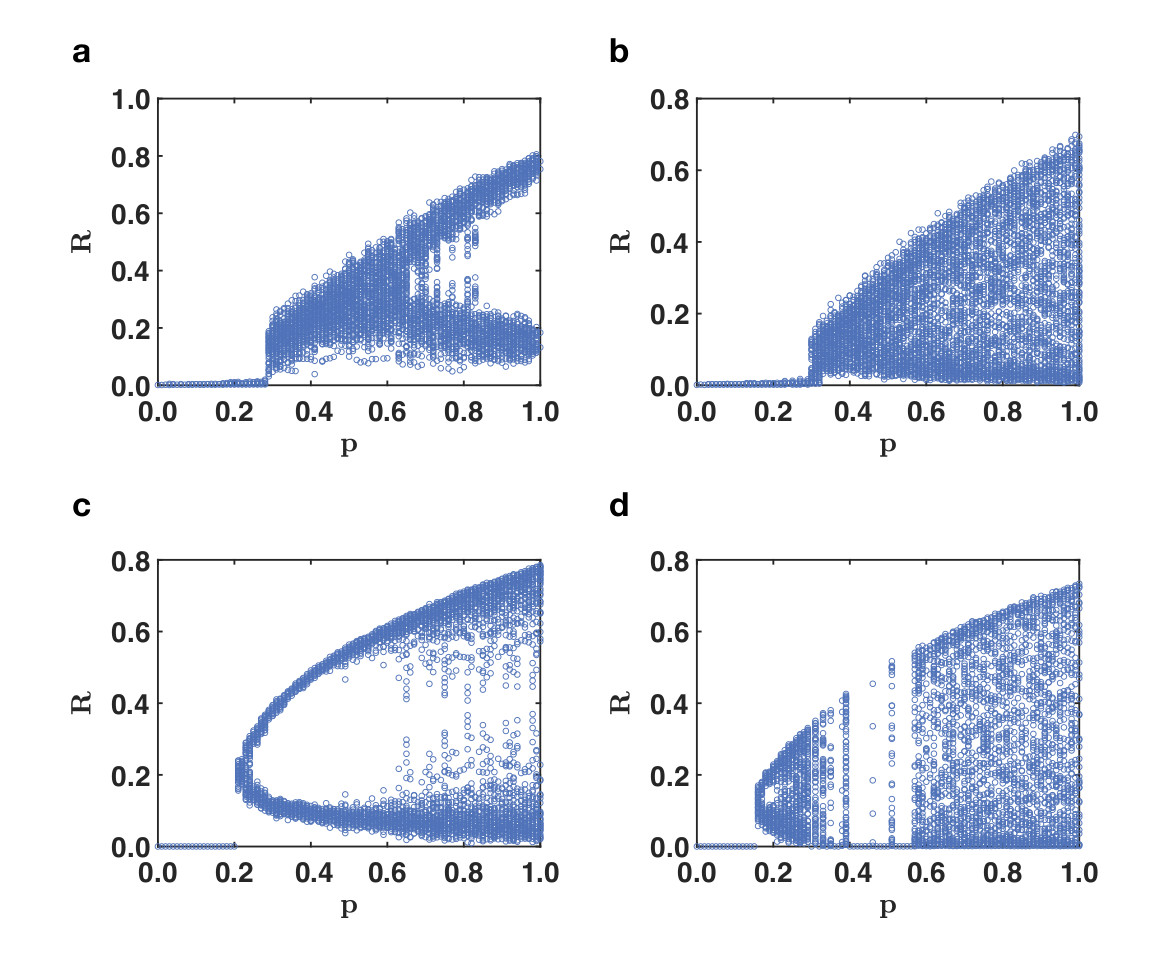
Fig. 4 | Triadic percolation induces blinking and chaos also in the connectivity of real networks. The phase diagram of triadic percolation on the mouse connectome (panels a,b) and the Human bio grid networks with radom triadic interactions (data available at [6]).
As in the Ising model introducing signed interaction is a game changer, and transform drastically the Ising model into a spin glass model [5], here we observe that the sign of triadic interactions dramatically changes the properties of percolation turning percolation into a fully fledged dynamical process. Indeed blinking and chaos of the order parameter of triadic percolation requires the presence of triadic interactions of negative sign, and by removing all negative triadic interactions triadic percolation always reaches a steady state, displaying a still interesting discontinuous hybrid transition but not a time-varying order parameter asymptotically in time.
Triadic percolation is robust also to generalization of the dynamics including time delays in the regulation of the activity of the links. This result shows that the observed phenomenology is general and not restricted to the simple definition of triadic percolation as a two step process.
In conclusion triadic percolation captures the dynamic nature of the giant component and network connectivity in presence of signed triadic interactions. These results drastically change our understanding of percolation and open new perspectives for studying networks with a time dependent connectivity as the one occurring in neuroscience and climate.
References
[1] Sun, H., Radicchi, F., Kurths, J. and Bianconi, G., 2023. The dynamic nature of percolation on networks with triadic interactions. Nature Communications, 14(1), p.1308.
[2] Grilli, J., Barabás, G., Michalska-Smith, M.J. and Allesina, S., 2017. Higher-order interactions stabilize dynamics in competitive network models. Nature, 548(7666), pp.210-213.
[3] Bairey, E., Kelsic, E.D. and Kishony, R., 2016. High-order species interactions shape ecosystem diversity. Nature communications, 7(1), p.12285.
[4] Boers, N., Goswami, B., Rheinwalt, A., Bookhagen, B., Hoskins, B. and Kurths, J., 2019. Complex networks reveal global pattern of extreme-rainfall teleconnections. Nature, 566(7744), pp.373-377.
[5] Mézard, M., Parisi, G. and Virasoro, M.A., 1987. Spin glass theory and beyond: An Introduction to the Replica Method and Its Applications (Vol. 9). World Scientific Publishing Company.
[6] Rossi, R. A. & Ahmed, N. K. The network data repository with interactive graph analytics and visualization. In Proceedings of the Twenty-Ninth AAAI Conference on Artificial Intelligence. http://networkrepository.com (2015).
Follow the Topic
-
Nature Communications

An open access, multidisciplinary journal dedicated to publishing high-quality research in all areas of the biological, health, physical, chemical and Earth sciences.
Related Collections
With Collections, you can get published faster and increase your visibility.
Women's Health
Publishing Model: Hybrid
Deadline: Ongoing
Advances in neurodegenerative diseases
Publishing Model: Hybrid
Deadline: Mar 24, 2026
Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in