According to Aristotle,

The whole is greater than the sum of its parts.

This ancient wisdom finds resonance in the study of complex systems that span from the atomic level to vast planetary scales. Such systems contain numerous interacting components, whose synergy cannot be simply derived from details of the parts, but arises from their mutual interactions, making it hard to model by traditional reductionist approaches. Consider chaotic systems, such as weather patterns, as an example. Their intricate and unpredictable nature classifies them as complex systems. While modeling such systems has proven to be an arduous task, they also possess intriguing and remarkable phenomena. A prime instance is a concept of "emergence", which occurs when a complex entity has properties or behaviors that its parts do not have on their own. One example is provided by ant colonies. While individual ants follow simple rules and have limited capabilities, a colony as a whole displays complex behaviors, such as building intricate nests, farming fungi, or herding aphids.

In the optical domain, a prominent example of complex systems is provided by chaotic optical microresonators, in which light exhibits chaotic ray dynamics such that a small deviation in the initial condition leads to an exponential divergence of trajectories [1]. Figure 1 demonstrates an example of optical chaos in a stadium-shaped cavity. Hundreds of light rays are launched towards almost the same direction inside the cavity. As time evolves, these rays start to separate from each other after traveling and being bounced by the boundary of the cavity. A long time later, they completely diverge and occupy the entire cavity, exhibiting a chaotic pattern.

The characterization and control of the optical fields in such chaotic resonators are usually intricate. Therefore, their response is typically modeled as a collective off-resonance background or a single low-quality-factor mode [3], even though in reality this response is associated with a very large number of individual resonances. Unlike conventional optical microresonators, however, the large modal density in chaotic photonic systems, as well as the complex overlap among different chaotic modes, makes it difficult to control and explore their overall dynamics, ruling out the new possible emergent photonic applications.

In our recent article published in Nature Physics [4], we leverage the non-Hermitian nature of a silicon stadium microcavity buried in silica and show that we can efficiently control such a chaotic cavity involving thousands of optical modes in the telecommunication wavelength band. Although non-Hermiticity in optical resonators has been widely studied to achieve extreme wave phenomena, including parity-time symmetry and exceptional points, they have been investigated so far only in simple systems. Specifically, we demonstrate the emergence of reflectionless scattering modes (RSMs), which is not only the generalization of the concept of coherent perfect absorption (CPA), but also a remarkable extension of non-Hermitian physics to wave scattering engineering. In short, RSMs are the steady-state solutions of the wave equation under one or more coherent incident waves, which can be posed as a non-Hermitian eigenvalue problem. These modes are physically realizable only when some or all these eigenvalues are real, at the corresponding frequencies, and only when the corresponding coherent eigenfunction is incident. This stringent requirement partially explains why the coherent wave control via RSMs and CPA has so far been limited to simple platforms by continuously tuning their design parameters.

The chaotic cavity and the experimental setup used in this work are shown in Fig. 2 (a). Two nanowaveguides are fabricated connecting with the stadium cavity to couple the light in and out of the cavity. Without sophisticated cavity designs or loss channel engineering, we show that RSMs arise massively in this stadium-shaped microcavity due to chaos-induced abundant modes. As shown in Fig. 2(b), many reflection zeros (eigenvalues mentioned above) fall on the real axis (black-dashed line).

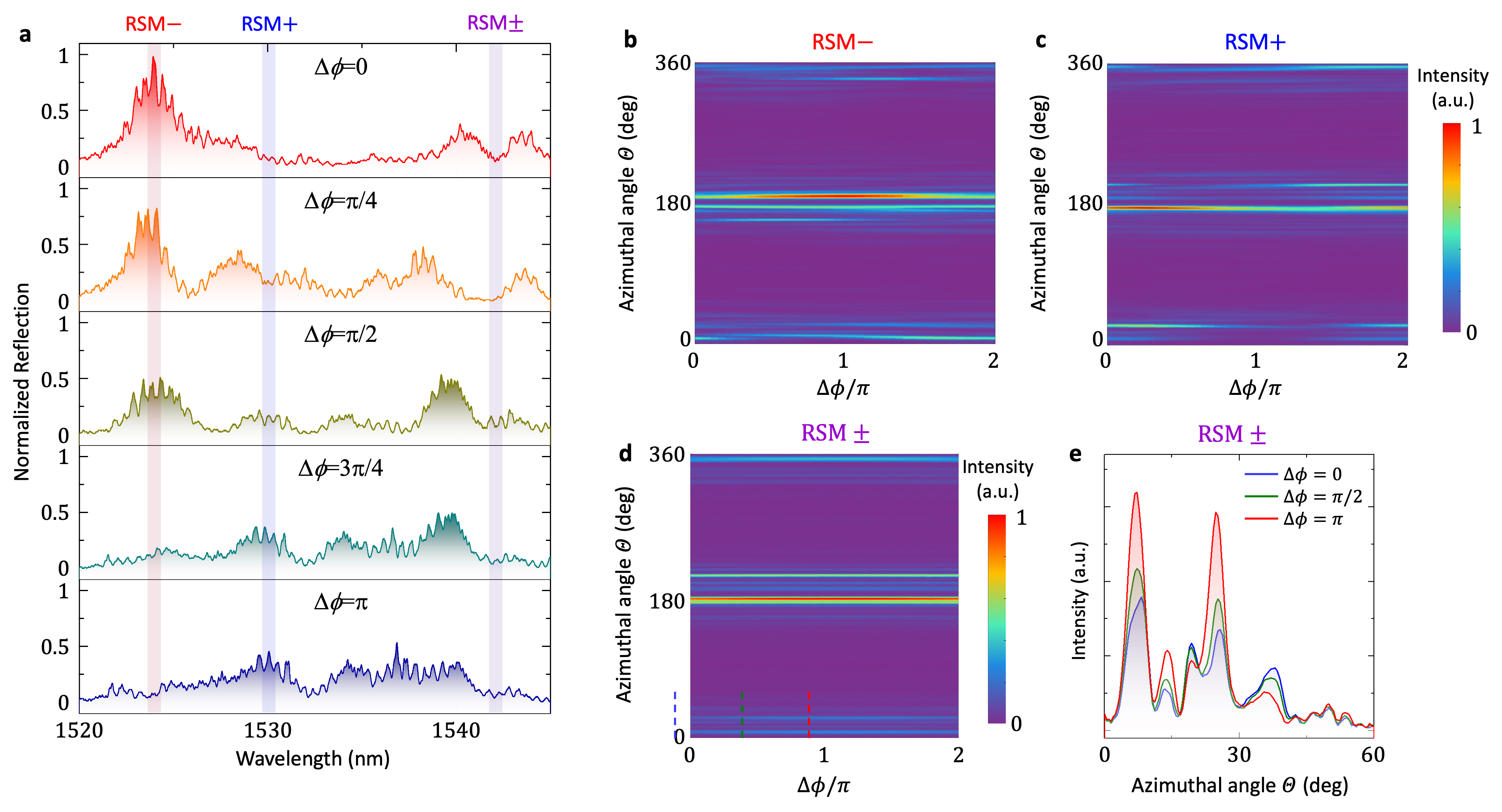
Experimentally, by tuning the relative phase of a pair of coherent excitation beams, we demonstrate the emergence of numerous chaotic RSMs, as shown in the reflection spectrum [Fig. 3(a)]. as well as their non-EP degeneracy (RSM). By taking advantage of these properties, we demonstrate the control of the far-field emission pattern emerging from the microresonator, as shown in Fig. 3(b-e).

This paper not only represents the first observation of RSMs in the optical domain, but it also sheds light on the universality of non-Hermitian physics beyond few-mode resonant systems, paving the way for new opportunities in the science and technology of complex nanophotonic systems by chaotic wave interference. Our work provides an ideal platform to investigate dynamic control of energy storage as well as anti-reflection phenomena in real-world scenarios involving highly spatial and spectral complexities. The underlying principles can find applications in various chaotic systems, ranging from chaotic microlasers, and cavity optomechanical systems, to chaos-based optical communications. Beyond this, these mechanisms and concepts may also be explored in other complex systems, including not only random scattering media, and random lasing, but also communication systems, and electronic systems.

For more details, please read our paper.

References

1. Cao, H. & Wiersig, J. Mod. Phys. 87, 61–111 (2015).
2. Datseris, G. Journal of Open Source Software 2, 458 (2017).
3. Yang, Q. F., et al. Rev. A 88, 023810 (2013).
4. Jiang, X., Yin, S., Li, H. et al. Nat. Phys. (2023). https://doi.org/10.1038/s41567-023-02242-w