The idea

One of the central questions in complex systems is the importance and role of scales, meaning how we need to set our lenses to better capture the properties of a system.  For instance, to understand the spreading of a virus across the population, we might need to pass from an international level to a national, regional, local scale, or vice-versa. This question is then—on the one hand—motivated by the emergence of macroscopic phenomena from the tapestry of microscopic interactions, and—on the other hand—by the frequent presence of heterogeneity in the microscopic interaction patterns of such systems. 

Attempts to reconcile these two elements have been phrased in the language of the renormalization group (RG), one of the cornerstones of modern theoretical physics. This language allows to study of a physical system at different scales (i.e. with different lenses), providing formal definitions for universality classes and scale-invariance. 

In the specific case of complex networks, efforts in this direction have recently been successful, giving rise to a rich class of methodologies for renormalization^1-6. Of particular interest is the approach by Villegas et al. ⁵, with its extension of the RG to general heterogeneous networks using information diffusion. The proposed (Laplacian) RG scheme, however, cannot describe systems beyond pairwise interactions, that is, systems characterized by higher-order (or group) interactions. A vast and still growing literature shows that such higher-order interactions are common across multiple domains (biology, sociology, etc.) and give rise to unexpected and rich dynamical phenomenologies. 

Therefore, for a complete characterization of complex systems, we need to generalize the RG scheme to include higher-order interactions.

The challenges

Following the idea of leveraging the process of information diffusion among the nodes of a graph, we needed to build a novel Laplacian Renormalization Group scheme that describes the structure and properties of arbitrary higher-order networks (hypergraphs, simplicial complexes, cell complexes, etc.) across scales. In particular, the main challenges can be summarized into the following two questions.

• How can we find order-specific properties of a system?
• If these properties are found, how can we adjust our lens to study the system?

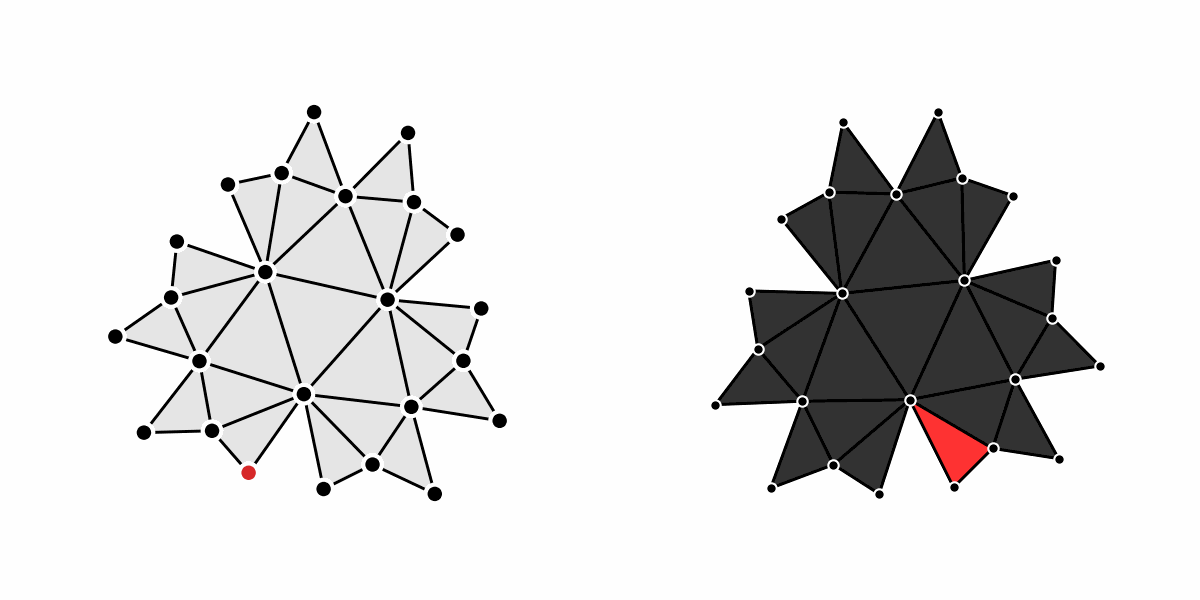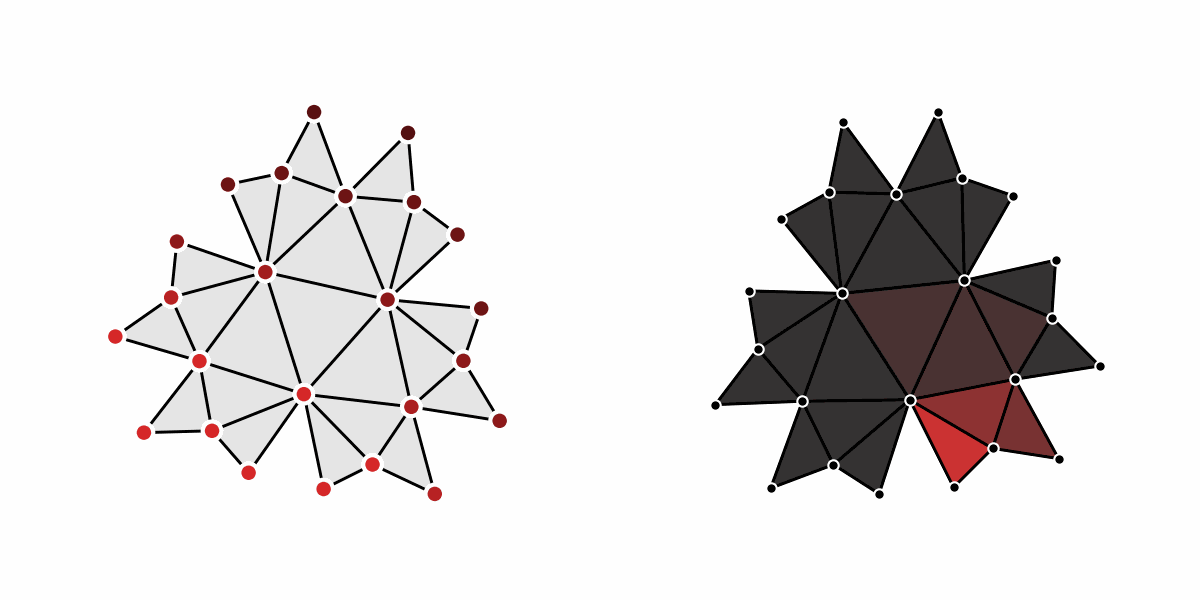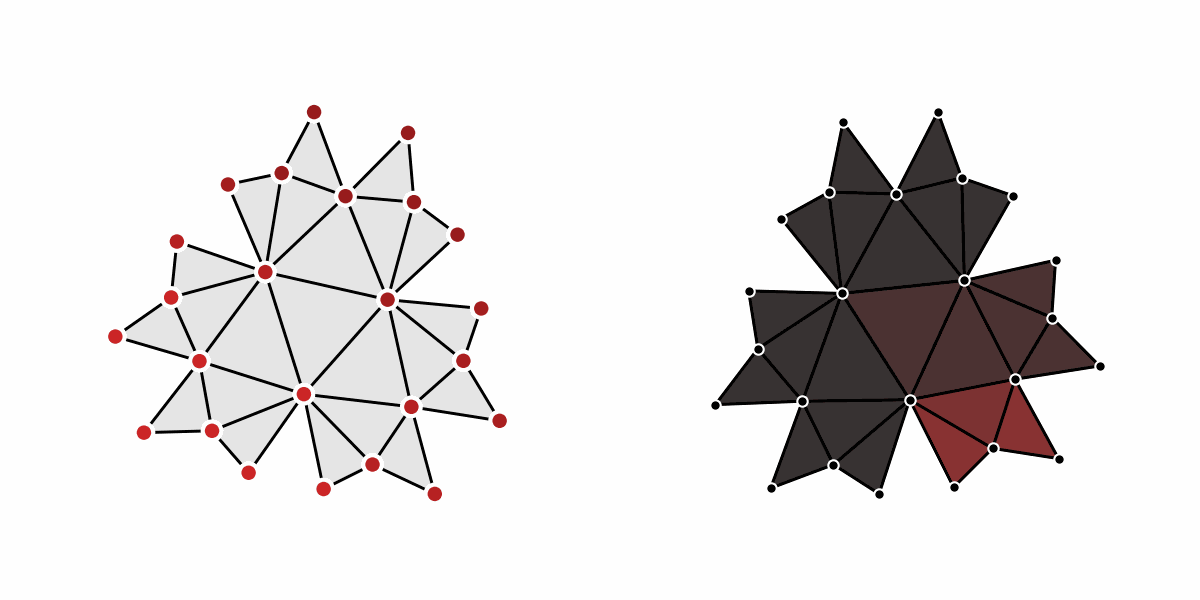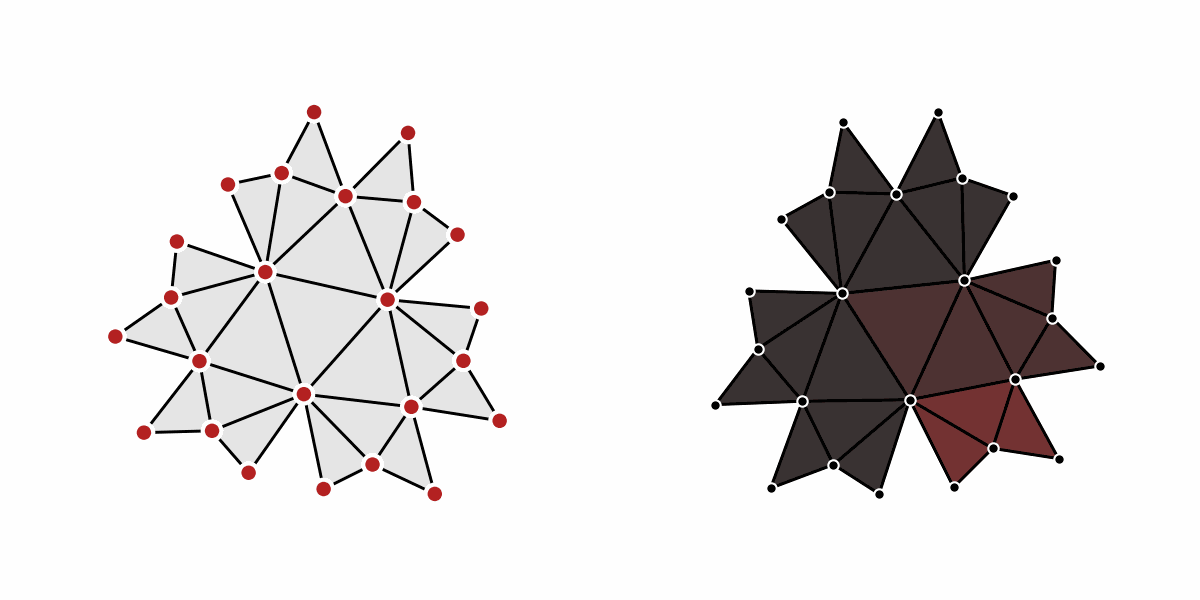
The first contribution

For standard networks, the description of a diffusion process is straightforward: information is placed on nodes and flows through the edges. Simplifying, the information spreads through people when they meet each other.

For higher-order systems, however, many more degrees of freedom are present.
Indeed, any higher-order system can support a set of different diffusion processes, each one related to a particular type of structural relation therein (e.g., flows between triangles via tetrahedra that contain them, or via shared edges). In other words, for example, if three researchers share a paper (3-order interaction), the results can be shared by each one of them (nodes) in a conference.

The natural extension for a diffusion process on higher-order networks is usually considered to be the so-called Hodge Laplacian operator. However, the diffusion processes generated by it are difficult to interpret from the physical point of view.

To overcome this problem, we built a support—or adjacency— graph derived from the original higher-order system which translates the higher-order diffusion into a standard—lower-order—one. Therefore, in the support graph, everything is reduced to information on nodes flowing through edges. Thus, we can take advantage of the Laplacian RG for heterogeneous networks to extract the properties of the system at the different orders.

The second contribution

To answer the second question, or to zoom-out—coarse-grain—the system, we simply identify blocks of interactions strongly connected by the diffusion process, to then collapse them into smaller ones. This results in a smaller and equivalent system.

The data

To ground our methods in the real world, we explored different domains and types of systems by analyzing  20 hypergraphs present in the recent toolbox XGI and 34 pairwise networks from the KONECT, ICON and the Network Data Repository (which we promoted to higher-order system using their clique structure). In total, we had systems from sociology (collaboration, school contacts and email networks), biology (gene, protein interactions and ecological networks), neuroscience (connectomes from different species) and infrastructure (road networks), which we organized into 6 macro-categories: social, collaboration, biology, connectome, ecological and infrastructure.

To find scale-invariant signatures in real-world data, we study the systems through the lens of our cross-order RG scheme. Summarizing the properties of scale-invariance of a system across multiple orders, we found that systems of similar nature show similar signatures. More interestingly, we found many systems displaying scale-invariant properties only at higher orders, which otherwise would not appear to be invariant from a traditional graph (low-order) perspective.  For instance, the metabolic network of the C. Elegans shows scale-invariance looking at diffusion processing taking place on triangles through nodes. The same happens for the network of A Song of Ice and Fire, which is a social network instead. Even more interestingly, also real networks—when promoted to higher-order systems—showed non-trivial structures hinting to the fact that also many of the systems we think and describe as networks might conceal deeper higher-order mechanisms. 

Final remarks

In summary, the central message of our work is that different kinds of relations between nodes or groups of nodes coexist in higher-order networks, and they need to be taken into account appropriately. Our cross-order Laplacian can capture these different structural organizations and identify higher-order characteristic scales. Some crucial properties of higher-order networks, like the informational scale-invariance, are clear only from the point of view of the relations between groups of nodes, being entirely invisible from the point of pair-interacting nodes. 

P.S.

The M&Ms would like to highlight here that the work had ups and downs, but the team was always supportive, nice, and fun to work with, even in difficult times.

References

1. Serrano, M. Ángeles, Dmitri Krioukov, and Marián Boguná. "Self-similarity of complex networks and hidden metric spaces." Physical review letters 100.7 (2008): 078701.
2. Rozenfeld, Hernán D., Chaoming Song, and Hernán A. Makse. "Small-world to fractal transition in complex networks: a renormalization group approach." Physical review letters 104.2 (2010): 025701.
3. García-Pérez, Guillermo, Marián Boguñá, and M. Ángeles Serrano. "Multiscale unfolding of real networks by geometric renormalization." Nature Physics 14.6 (2018): 583-589.
4. Garuccio, Elena, Margherita Lalli, and Diego Garlaschelli. "Multiscale network renormalization: Scale-invariance without geometry." Physical Review Research 5.4 (2023): 043101.
5. Villegas, Pablo, et al. "Laplacian renormalization group for heterogeneous networks." Nature Physics 19.3 (2023): 445-450.APA
6. Zheng, Muhua, et al. "Geometric renormalization of weighted networks." Communications Physics 7.1 (2024): 97.