The story of our paper began in the mid-2020 when a colleague forwarded me an article and the associated video on the observation of branched flow of light. I was impressed by the ingenuity of the experiment and by the elegance of the phenomenon described therein. It showed that light waves travelling in media (in this case, soap bubbles!) with even a small amount of spatially correlated randomness show the phenomenon of branched flow where the light waves deflect and interfere to form locations of extreme amplitudes. One is able to predict the average location of the first of such extreme focussing events. The average distance (l_f ) of occurrence from that of launch has a power law scaling with exponent -1/3 with respect to a quantity describing the severity of randomness (<h²>). This was particularly interesting. There is also a linear scaling of this distance with respect to the correlation length of the random field (l_c). My interest was further piqued when I discovered that branched flows have been reported in a wide variety of other physical contexts ranging from tsunami waves, sounds in the ocean to electron gas. This suggested a certain universality of the phenomena.

Since, I am an elastictian by training, it naturally got me wondering about the possibility of branched flows in elastic waveguides. I decided to focus on bending waves in thin plates as this is one of the most important modes of wave propagation in thin elastic sheets. After discussing with my supervisors (Atul and Neil), we realized that demonstrating the existence of branched flows in elastic structures could be a significant result since most of the other works on branched flows (with the possible exception of electron gas) were governed by the classical non-dispersive wave equation despite the vastly different physical contexts and length scales involved. On the other hand, bending waves in plates are governed by the biharmonic wave equation. This equation is appreciably different from the classical wave equation since bending waves are dispersive i.e., the speed of waves is dependent on their wavelength as shorter waves travel faster, unlike the classical wave equation where all waves travel at the same speed regardless of their wavelengths.

Convinced of the merit of such research, I set about conducting numerical experiments into this phenomenon using finite element simulations. The preliminary results were encouraging. We could see the emergence of branches and extreme amplitudes even with the introduction of tiny variations in the thickness profile.

While we had the qualitative result in place, demonstrating the emergence of branches, the quantitative result, i.e., the scaling of the location of the first focusing event with the random field statistics, would not be available unless we conducted more simulations. Around 4800 more simulations! We needed those many simulations to have enough data to study the behaviour of the mean values. To do this, I parametrized the FE code that I had written to obtain the preliminary results and proceeded to amend it so that it could be run on the High Performance Clusters (IRIDIS-5) at the University of Southampton.

Concurrently, we also started working towards the analytical proof and an independent numerical verification using ray approximations of the plane wave transmission. As we went through the previous literature on the subject, we realized that the proof involved ideas borrowed from stochastic calculus and statistical mechanics. While I developed a working understanding of the tools required, I found help from an unexpected source - a friend (Dhruv Singal) working on a PhD in Finance! He was able to help me with aspects of stochastic calculus that I was unfamiliar with whereas he was familiar with it from its application to modelling financial markets. Soon enough, we were able to derive the ray equations and develop the analytical proof. They confirmed the scaling l_f ∝ l_c <h²>^-1/3 which interestingly is the same as that observed in other physical contexts.

Then began the wait for the FE simulation results to roll in. This took some time since we had ~4800 simulations each taking between 15 minutes to 8 hours on 64 cores! As I started processing the results, I noticed that while there was a power law scaling with respect to <h²>, the value of the exponent was wrong. This was puzzling. This disagreed with both analytical and numerical ray simulation results. More FE simulations just strengthened this wrong scaling trend. This led me to comb through my code in detail and I discovered that I had a bug in the code generating the random field. Once I fixed it, the FE simulation results fell right into place!

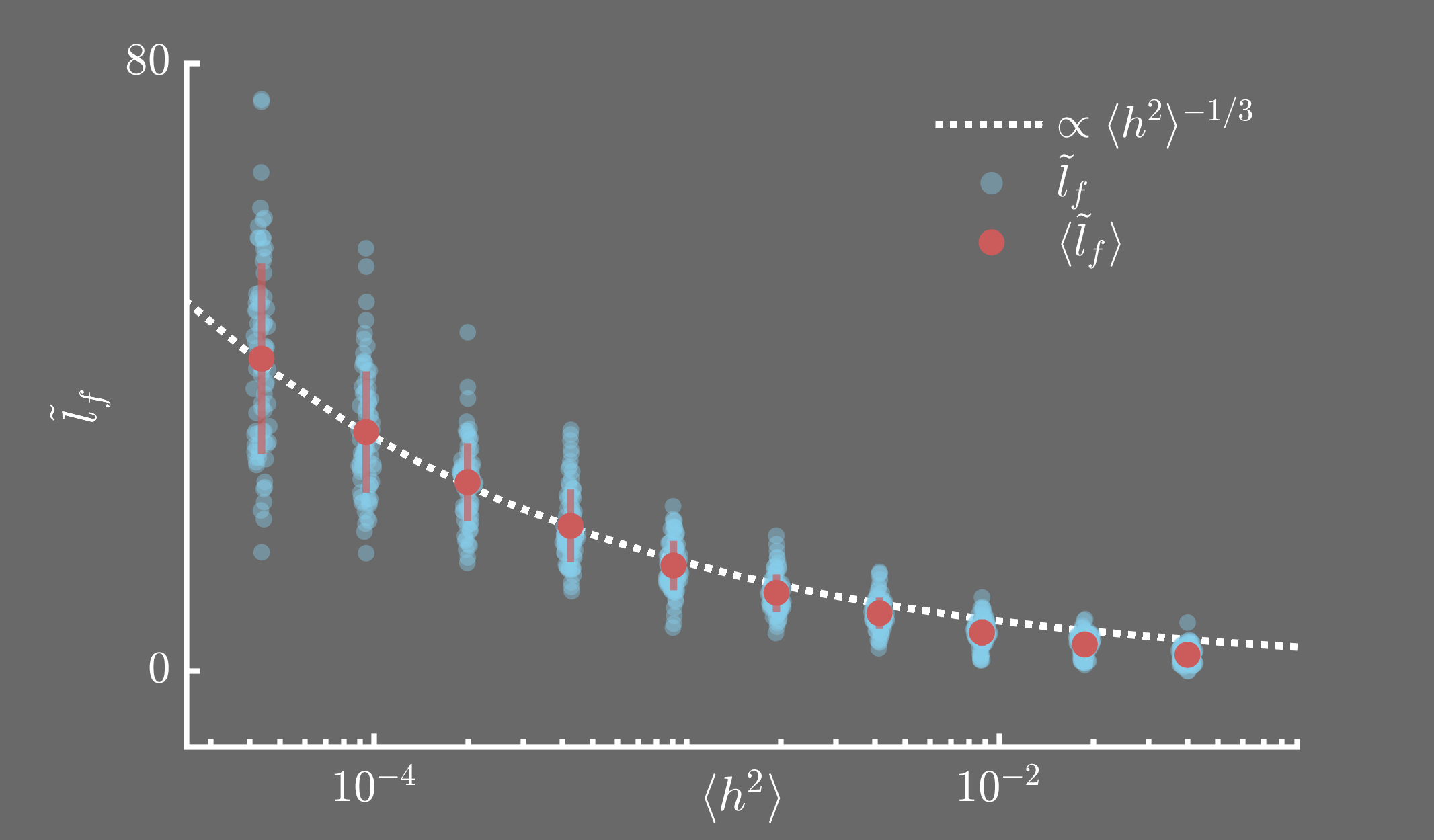
This work adds flexural waves in thin elastic structures to the growing list of physical domains in which branched flows have been observed. In the future, we would like to explore the true extent of the universality of branched flows of elastic waves through analytical and numerical investigations.

With the results written up, our manuscript was accepted for publication in Communications Physics. We are very thankful for the feedback and comments from the reviewers and editors.