Emergent Phases, Unconventional Magnetotransport, Anomalous Hall Effect and Magnetic Anisotropy in a Quasi-2D vdW Ferromagnet Fe4GeTe2
Published in Physics

The discovery of quasi-two-dimensional van der Waals (vdW) magnets has provided a novel platform for exploring low-dimensional magnetism and its potential applications in two-dimensional (2D) spintronic devices. Recent advancements focus on the family of iron-based vdW magnets, including FenGeTe2 (n = 3, 4, 5), particularly Fe4GeTe2 and Fe5−xGeTe2, due to their ferromagnetic transition temperature (TC) approaching room temperature. In the 2D limit, the Mermin-Wagner theorem suggests no spontaneous magnetic order at finite temperature; however, the uniaxial magneto-crystalline anisotropy in these vdW systems stabilizes long-range order against thermal fluctuations. The magnetism in these materials is rather complex in nature, differing from typical ferromagnets, due to the presence of different inequivalent Fe atoms in the unit cell. More recently, it has been reported that the Fe4GeTe2 single crystal is a metallic ferromagnet that exhibits a change in easy axis of magnetization when cooled below ∼ 120 K (TSR), termed as the ‘spin reorientation transition’ (SRT), along with a TC ~ 270 K, making it magnetically unique from the other 2D magnets.
In this study, through a combination of detailed electronic, magneto-transport [1], first-principles calculations [1], and electron spin resonance (ESR) spectroscopic measurements [2], we uncover emergent electronic phases in quasi-2D vdW ferromagnet Fe4GeTe2.
By conducting transport experiments [1] on exfoliated nanoflakes of Fe4GeTe2 and employing first-principle calculations [1], we identify two distinct electronic transitions in the thin limit of Fe4GeTe2, measured and compared in two distinct exfoliated devices with thicknesses of ∼ 95 nm (D95) and ∼ 16 nm (D16). The first transition near the TSR is marked by a sharp resistivity drop and a sign change in the ordinary Hall coefficient, alongside maximum negative magnetoresistance (MR) and maximum anomalous Hall conductivity [1]. A second, previously unknown transition occurs around 40–50 K (TQ), where the Hall coefficient changes sign again, resistivity shows a quadratic temperature dependence, and MR becomes positive [1]. The analysis [1] exposes competing inelastic scattering processes, while the DFT-based calculations propose two magnetic phases, elucidating observed magnetotransport phenomena.
ESR spectroscopic study [2] on Fe4GeTe2 provides quantitative insights into the non-trivial temperature evolution of the magnetic anisotropy - one of the main contributors to the stabilization of the magnetic order in the low-dimensional systems. At high temperatures, the total magnetic anisotropy (MA) is dominated by the demagnetization effect, with a slight contribution from the counteracting intrinsic easy-axis MA, whose growth below a characteristic temperature Tshape ≈ 150 K renders the sample seemingly isotropic at TSR [2]. Below TQ, the intrinsic MA becomes more complex. Thus, this spin reorientation results from the competition between the intrinsic easy-axis anisotropy of Fe4GeTe2 and the (extrinsic) shape anisotropy of its plate-like shape [2]. Interestingly, observed characteristic temperatures align in ESR and transport measurements [2], highlighting inherent coupling between magnetic and electronic degrees of freedom. Such a plausible mutual dependence of the spin waves and the charge carriers can open a possibility to tune the transport properties of Fe4GeTe2 by controlling the magnetic excitations, and vice versa, which could find an application in the next generation of spintronic devices.
Details of Fe4GeTe2: High-quality Fe4GeTe2 single crystals were grown [1] via the chemical vapor transport (CVT) method using I2 as a transport agent. A single layer of Fe4GeTe2 consists of seven atoms: Fe1 and Fe2 arranged on both sides of the Ge atomic plane, directly connected to Te atoms on both sides, as shown in Figure 1a. The stacking of these Fe4GeTe2 monolayers forms a rhombohedral structure with space group R-3m. Single crystals of Fe4GeTe2 exhibit a ferromagnetic TC ≈ 270 K, where dM/dT shows a minimum, followed by a spin reorientation transition at TSR ≈ 120 K, below which the out-of-plane magnetization exceeds the in-plane value (see Figure 1c).
Figure 1. (a) Crystal structure of Fe4GeTe2. (b) Schematic of Hall bar device (c) Temperature-dependent dc magnetization data (d) Temperature-dependent resistivity (ρxx) of Fe4GeTe2 device. Theoretical fits in different temperature regimes are marked in red, purple, and cyan colors. Inset left: Hall bar device image. Inset right: ρxx vs T2 curve shows a clear change of slope above ~ 40 K. Source: Ref.[1]
Experimental Results:
Resistivity: The in-plane resistivity (ρxx) of Fe4GeTe2 exhibits a metallic behavior (see Figure 1d) (conductivity at TC ~ 9.6 × 105 Ω−1m−1), with almost negligible change near the ferromagnetic transition. However, the resistivity falls dramatically below SRT. ρxx shows two anomalies, near TSR (∼120 K) and TQ (∼ 40 - 50 K), indicated by the clear kinks in the dρxx/dT curve. The analysis exposes competing inelastic scattering processes. At low temperature below TQ, ρxx follows a perfectly quadratic behavior (ρxx ∝ T2), corresponding to electron-electron (e-e) scattering, confirmed by its magnetic field independent behavior below TQ, suggesting the Fermi liquid behaviour [1]. In the intermediate range (60-130 K), both electron-phonon (e-p) (ρ ∝ T) and electron-magnon scattering (ρ ∝ T2) contribute, confirmed by the strong magnetic field dependence [1]. At higher temperatures above 190 K, only the e-p scattering (ρ ∝ T2) mechanism dominates [1] .
Magnetoresistance: The high-field (9 T) MR [1] exhibits several interesting features (Figure 2b). MR is predominantly negative in the range between ∼ 40 K to 300 K and maximum near the SRT (TSR), due to the suppression of e-m scattering under external magnetic fields, being ∼ 11% for D95 and ∼ 21.2% for D16 (Figure 2b). Comparatively large negative MR for D16 is possibly due to the enhanced FM interaction and reduced orbital scattering in the thinner limit [1]. Below TQ, MR is small but positive (∼1.8% for D95 and 0.6 % for D16 at 1.6 K), quite unusual for a metallic ferromagnet. By fitting the positive MR at low temperatures (see Figure 2a inset), we observed an almost B2 dependency of MR, being closer to the behavior of a typical metal having pure orbital contributions [1]. To test whether the electronic properties are isotropic, angle-dependent transverse magnetoresistance (TMR) measurements at 9 T were performed at various temperatures, as shown in Figure 2c. Below 100 K, the low-temperature data exhibit a cosine-like behavior, while above TSR, a 90° phase shift occurs, indicating a change of the magnetic easy axis from the c-axis to the ab-plane with increasing temperature.
Figure 2. (a) Magnetoresistance at different temperatures. Inset: MR shows B2 dependency at 1.6 K. (b) Temperature-dependent MR is plotted for two devices with applied field 9 T. (c) Angle-dependent TMR at 9 T. Source: Ref.[1]
Hall measurements: Typically, the Hall resistivity (ρxy) of a ferromagnetic material can be described by the empirical formula: ρxy = ρxyOHE + ρxyAHE = R0B + μ0RSM. Here, the first term is the ordinary Hall resistivity, and the second term represents the anomalous Hall resistivity. From Hall data (see Figure 3a) [1], ordinary Hall coefficient (R0) shows the sign change in the proximity of TSR and TQ (see Figure 3b), indicates the change in the majority carriers from holes (positive) to electrons (negative), possibly due to Fermi surface reconstruction or a Lifshitz-like transition occurring as a result of SRT. Almost identical behavior was observed [1] in both devices, D95 and D16. The anomalous Hall coefficient (RS) shows non-monotonic behavior, reaching a maximum near 140 K and decreasing sharply below the SRT (see Figure 3c). A material-specific scaling factor, SH, defined as RS = SHρxx², varies weakly above the SRT but changes significantly below it, reflecting a complex interplay between resistivity and magnetism. The DFT-based theoretical calculations [1] suggest the generation of new electron and hole Fermi surface pockets, which well explain this unusual sign change and enhanced metallicity near TSR [1]. Also, we obtained larger anomalous Hall conductivity, angle, and scaling coefficient near TSR [1], making it superior to other 2D magnets.
Figure 3. (a) Magnetic field dependence of Hall resistivity at temperatures from 10 K to 300 K. (b) Temperature dependence of the ordinary Hall coefficient (R0) for the two devices (D16 and D95). (c) Temperature dependence of the anomalous Hall coefficient RS and the scaling coefficient SH. Source: Ref. [1]
ESR measurements: The ESR spectroscopy is a unique tool [2] for its extreme sensitivity to magnetic anisotropies that enables a straightforward measurement and accurate quantification of the MA parameters of the studied magnetic material. Moreover, the direct measurement of the magnetic excitations of the studied material allowed us to address the dynamic aspects of the magnetism.
For all magnetic field orientations, the ESR spectra of Fe4GeTe2 consist of a single resonance line, with shoulders appearing at certain temperatures [2]. Representative spectra are shown in Ref. [2]. The extracted resonance field Hres is plotted as a function of temperature for both H || ab and H || c configurations (see Figure 4a). The maximum deviation of Hres from the expected isotropic paramagnetic resonance field (Hrespara) occurs near 200 K. It crosses Hrespara near Tcross, indicating the change of the type of total anisotropy below and above Tcross. Although Hres decreases above this temperature, a noticeable shift remains at 300 K, about 30 K above the TC. This indicates that up to 300 K, ~30 K above TC, the total anisotropy field doesn’t vanish due to the short-range correlations, signature of a 2D spin system [2].
The extracted total MA field Ha from all measurements is plotted as a function of temperature in Figure 4b. The total MA field [2] is given by Ha = Hint + HD over the entire measurement temperature range. Here, Hint is the intrinsic (magneto-crystalline) anisotropy field, and HD = 4πNMS is the shape anisotropy field (coming from demagnetization effect due to its plate-like shape). To investigate the origin of the measured Ha, we calculated the expected HD [2] at different temperatures using N ≈ 0.71, estimated from the sample dimensions and its saturation magnetization MS (see Figure 4b). As observed [2], in the temperature range from 300 K to approximately 150 K, the Ha matches the sign, temperature dependence, and magnitude of the calculated HD. This indicates that for T > Tshape ≈ 150 K, the dominant contribution to the total MA of Fe4GeTe2 arises from the shape anisotropy, with a minor contribution from the opposing intrinsic MA of an easy-axis type [2]. However, its growth with decreasing temperatures (below Tshape) counters the HD, eventually leading the sample to appear isotropic near TSR (~ at Tcross) (see Figure 4b). Below Tcross, the easy axis intrinsic MA dominates over the demagnetization effect [2]. Furthermore, just below TQ (∼50 K), the intrinsic MA becomes even more complex, which cannot be explained by conventional spin-wave theory [2].
Thus, we have found that this spin reorientation results from the competition between the intrinsic easy-axis anisotropy of Fe4GeTe2 and the (extrinsic) shape anisotropy of the plate-like crystal [2]. Importantly, all the characteristic temperatures identified in the ESR experiment align with those observed in transport measurements (see Figure 4c), suggesting an inherent coupling between magnetic and electronic degrees of freedom in Fe4GeTe2 [2].
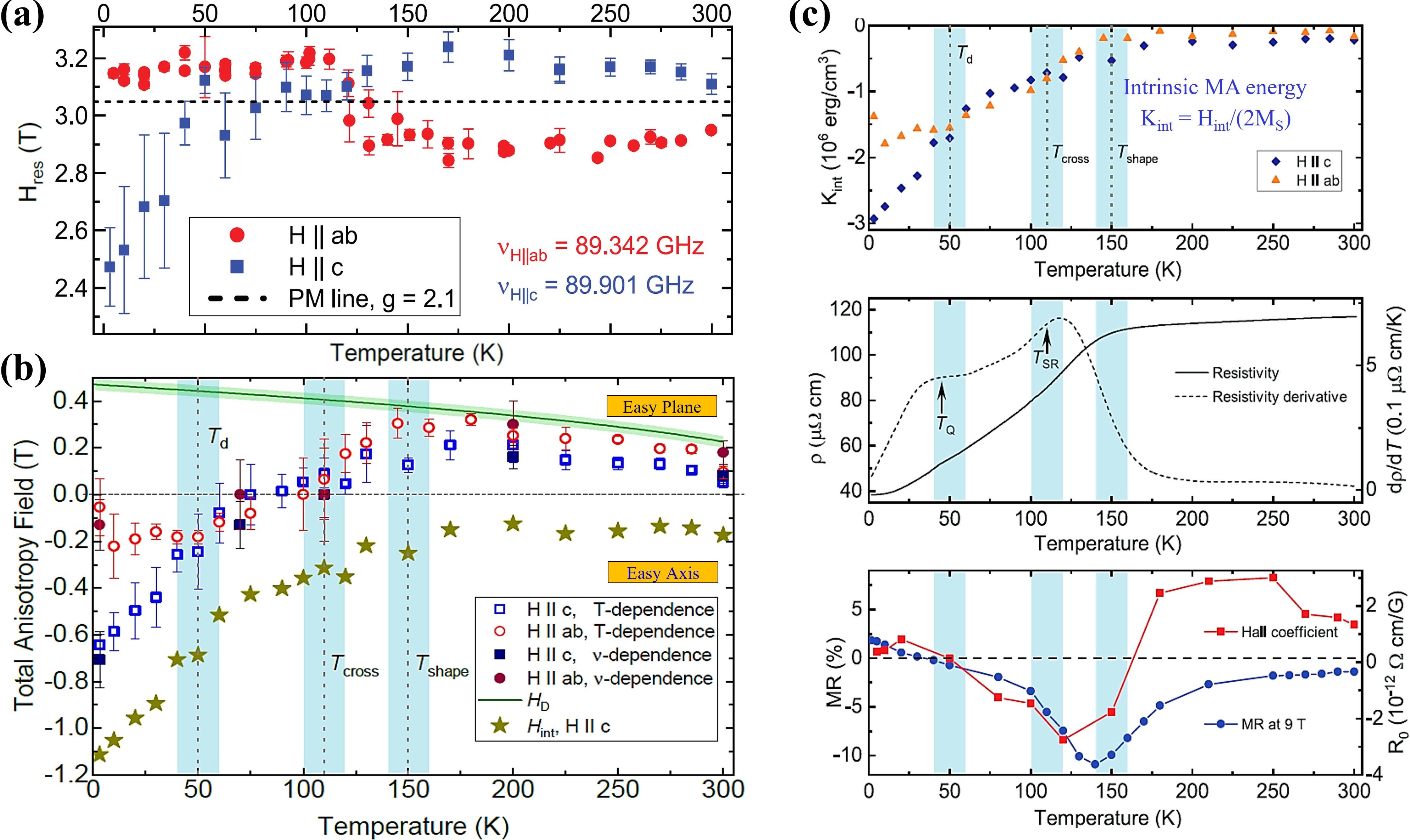
Figure 4. (a) Resonance fields as a function of temperature measured in H∥ab and H∥c configurations at w ≈ 90 GHz. (b) Total anisotropy field Ha as a function of temperature. (c) Temperature evolution of the intrinsic MA constant Kint estimated from the measurements in the H∥c (diamonds) and H∥ab (triangles) configurations and alignment of the characteristic temperatures matching with transport data. Source: Ref. [2].
Read the full papers here:
References:
[1] R. Pal et al., “Spin-reorientation driven emergent phases and unconventional magnetotransport in quasi-2D vdW ferromagnet Fe4GeTe2”, npj 2D Materials and Applications, 8, 30, 2024, www.nature.com/articles/s41699-024-00463-y
[2] R. Pal et al., “Disentangling the Unusual Magnetic Anisotropy of the Near-Room-Temperature Ferromagnet Fe4GeTe2”, Advanced Functional Materials, 34, 2402551, 2024, https://doi.org/10.1002/adfm.202402551
Follow the Topic
-
npj 2D Materials and Applications

This journal publishes papers on the fundamental behavior, synthesis, properties and applications of existing and emerging 2D materials.
Related Collections
With Collections, you can get published faster and increase your visibility.
Sensing with 2D Materials
Publishing Model: Open Access
Deadline: Dec 19, 2025
2D Materials for Integrated Electronics
Publishing Model: Open Access
Deadline: Apr 18, 2026





Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in