From curiosity to unconventional findings
Published in Physics

“What about measuring stimulated Brillouin scattering in liquid-core capillary fibers?” was the initial question that Birgit, Mario and Markus asked themselves several years ago, inspired by our colleague Alessandro. Curiosity was the main driving force for the project. It sounded promising to achieve strong optoacoustic interaction in a new exciting platform. Moreover, we wanted to gain understanding of the thermodynamic regimes and optical properties in fully-sealed liquid core optical fibers (LiCOF).
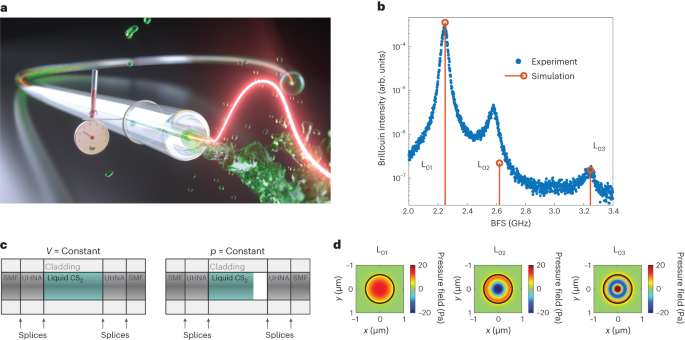
In measurements with carbon disulfide (CS2) filled LiCOF we found that indeed the gain was extraordinarily high and the Brillouin spectrum was non trivial compared to classic single mode fibers. Many modes arise at different frequencies and by comparing to our simulations it was clear that we see many prominent acoustic modes. This is because, beside optical guidance, in this scheme the LiCOF also provides acoustic guidance.
This knowledge became vital as we performed integrated SBS analysis while partially heating the LiCOF. This provides the full optoacoustic response integrated along the fiber under test. What we expected was a change in the Brillouin frequency shift (BFS) as the temperature of the fiber increases, but instead we saw even more peaks arising in the spectrum at completely new frequencies (Figure 1 - Manuscript Figure 2b). We wanted to understand the thermodynamic behavior of this new type of fiber. Numerical simulations suggested that the temperature is not a global parameter. By heating one half of the fiber instead of the whole, the temperature in the other half would stay the same, but this theory has not been measured experimentally yet.
.png)
Brillouin Spectrum at room temperature (blue) and for a half-heated fiber (orange). Multiple peaks arise as two influences change the Brillouin frequency shift: global pressure increase leads to an upshift (green arrow) and local temperature increase leads to a downshift (red dashed arrow).
We then used our expertise in high resolution localized Brillouin measurements and analyzed the behavior with frequency modulated Brillouin optical correlation domain analysis (BOCDA). When evaluating the spectrum along the LiCOF with centimeter resolution, it turned out that the part where we heated it actually was not changing in frequency. Instead, the part that we did not heat changed significantly. This turns out to resolve the riddle of the global or local influence of temperature, as there was a very clear jump in BFS from the heated to the non-heated part. It turned out, we were subject to an unlikely coincidence: for the chosen heating ratio, the two effects of frequency upshift due to pressure and frequency downshift due to temperature canceled each other out almost exactly. Thus, the heated part did not change while the non-heated part did, due to global increase of pressure.
With this understanding, the door was open for us to achieve full control over the thermodynamics in this state and individually tune temperature and pressure inside the fiber. So far though, pressure changes were known, while the absolute pressure value needed a calibration by cooling down to the point where the pressure was zero. At this point one would naturally expect that the liquid column breaks up and the fiber enters the isobaric state. In this state, a gas gap exists, there is no optical transmission and the pressure is approximately constant at the vapor pressure of CS2(approx. 1 bar).
This is where things became particularly interesting: When cooling down (follow the blue curve in Figure 2 - Manuscript Figure 4c), the pressure was decreasing as expected and transmission stayed constant, but the fiber just did not “want” to collapse into the isobaric state and the pressures we calculated seemed unreasonably high at room temperature. Only when heating a small part above the boiling point of CS2, a drop in transmission occurred, indicating a change in the state. This coincided with a large jump of the BFS to higher frequencies, indicating an increase of pressure, as the temperature was set and fixed. Because there is no transmission in that state of the fiber, Brillouin scattering analysis truly shines as it allows us to investigate the noise initiated backscattered light and thus neither needing a seed nor access to the second side of the fiber. Consecutive heating, now to be assumed in the isobaric state, behaved as expected: Only influenced by the temperature as the liquid can freely expand, the BFS moves to lower frequencies, until it recombines and the transmission is restored. At that point we had two approaches to an explanation: The first model assumed one bar pressure at the temperature of cavitation, thus explaining why it occurred there. The drawback was, one has to drop the assumption that in the isobaric state the pressure is not constant as they have to match at the recombination point where the two states are indistinguishable. The second model assumed the recombination point to be at one bar in both states. This preserves the isobaric state assumption but assumes that the pressure is then constant at one bar in both states as well. The BFS instead is then required to behave unreasonably nonlinearly with little change of pressure (BFS(p(T))), such that it appears linear when plotting BFS versus temperature, especially around the recombination point in the isochoric regime, where the BFS curve was without any change in slope. Both approaches were quite unsatisfying as explanations.
The breakthrough occurred when we looked deeper into the expectations of the change in BFS due to T and p(T) by looking into literature values and simulating what we observed. During implementation of the Δp ∝ ΔT, the natural relation preal = max(0,C*T+p0) was introduced. Of course, the pressure is always positive. A question arose: Why?
.png)
Figure 2 (Manuscript - Figure 4c)
The Brillouin frequency shift is shown in the isobaric (red curve) and isochoric (blue curve) states by first cooling down the LiCOF followed by switching to the isobaric regime by cavitation due to local heating. Negative pressures are maintained down to –300 bar.
By dropping this condition in the isochoric state, the system was described in a simple and elegant way: When cooling down below the recombination point, the pressure just switches sign. For a liquid, which experiences strong adhesive and cohesive forces compared to a gas, this matters little, as it would for a solid. Thus, the behavior continues linearly, explaining the linear BFS around the combination point. With this model the jump at cavitation can be explained as well, as a breakdown of the liquid column by punctual heating leads to a bubble of gas. This cannot “pull” on the liquid, while the liquid “pulls” on the gas, expanding the bubble even further, until vapor pressure is reached. The pressure then is higher than the negative pressure before which explains the big jump in BFS and stays constant with increasing temperature until the recombination point is reached.
Previous works on negative pressure confirmed this idea and made clear: it is not trivial to reach such substantially low negative pressures, showing huge potential to investigate nanoliter amounts of liquid, potentially toxic like CS2, at extreme but well controlled and stable conditions, using all the liquid in the optoacoustic interaction. In addition, the BFS is highly tunable (40 %) and shows a large gain of 32 (Wm)-1. We find that the story behind this work is exemplary for the situation, when one looks for a result, getting confused half way by unexpected behavior, but pursues the bumpy road of deep understanding, just to discover something even more remarkable and interesting.
Follow the Topic
-
Nature Physics

This journal publishes papers of the highest quality and significance in all areas of physics, pure and applied.


Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in