From Theory to Application: Improving Numerical Algorithms for Reaction-Diffusion Equations Through Lyapunov's Framework
Published in Mathematics

Reaction-diffusion equations are fundamental in mathematical modeling, particularly in systems with critical local interactions and spatial diffusion. These equations describe how the concentration of one or more substances distributed in space changes under the influence of local chemical reactions and diffusion processes. However, traditional numerical methods often face significant challenges regarding stability and consistency, particularly when simulating scenarios involving multiple interacting species in complex environments.
Addressing Stability and Consistency Challenges
Stability in numerical methods is paramount, especially in reaction-diffusion equations where small perturbations can lead to vastly different outcomes. When modeling phenomena such as the spread of an epidemic or a tumor's response to treatment, having a stable numerical scheme ensures that the results are reliable and meaningful. In our research, we address these critical issues by introducing a systematic framework for developing fully discrete schemes that preserve the stability properties of continuous models. By leveraging Lyapunov's method—a powerful tool in stability analysis—we ensure that our numerical methods yield accurate results while avoiding spurious solutions. This approach helps us maintain fidelity to the continuous dynamics while enabling robust numerical simulations.
The Importance of Reaction-Diffusion Equations
By enhancing numerical simulation techniques, our work aims to ensure stability and accuracy in these critical applications.
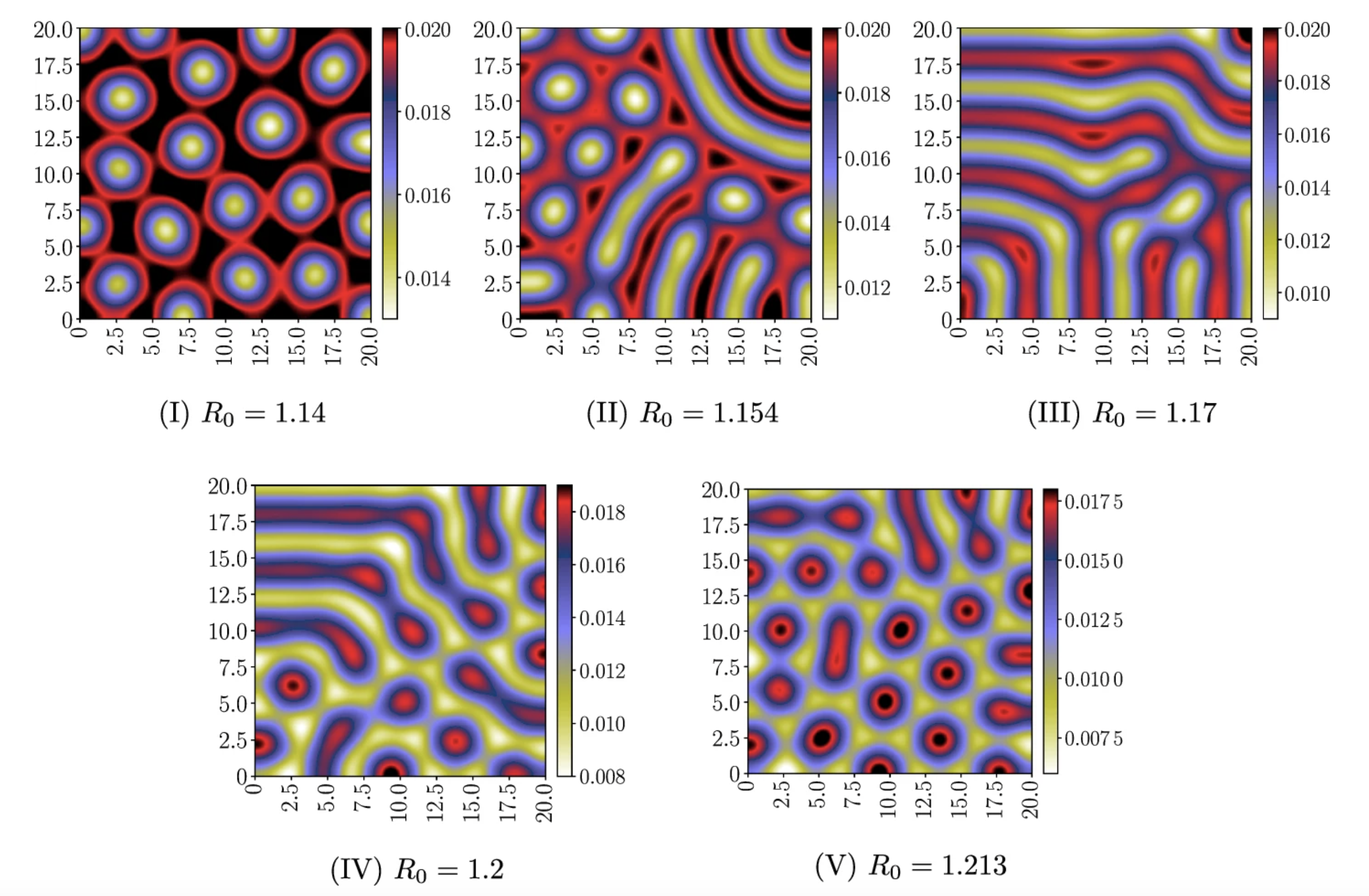
The Role of Spatial Factors in Epidemic Models
Epidemic models that neglect spatial factors often oversimplify the complexities of disease spread. For example, diseases can exhibit different behaviors in urban versus rural settings due to variations in population density and movement patterns. Our fully discrete Lyapunov-consistent discretizations, which account for both spatial and temporal effects of models governed by reaction-diffusion partial differential equations, lead to more accurate predictions of how an epidemic might unfold over time. This enhanced modeling capability is crucial for public health officials, who rely on robust models to devise effective intervention strategies such as vaccination campaigns or social distancing measures.
By employing our advanced numerical methods, we can simulate various scenarios and assess the potential impact of different interventions in real-time. This capability is crucial for making informed decisions during outbreaks, ultimately helping to manage healthcare resources more effectively.
Applications in Oncolytic Virotherapy
Another fascinating application of our work lies in oncolytic virotherapy, an innovative treatment approach that utilizes viruses to infect and destroy cancer cells selectively. Modeling the dynamics of oncolytic viruses alongside tumor growth is inherently complex, involving nonlinear interactions between multiple species, including tumor cells, immune responses, and the therapeutic virus itself.
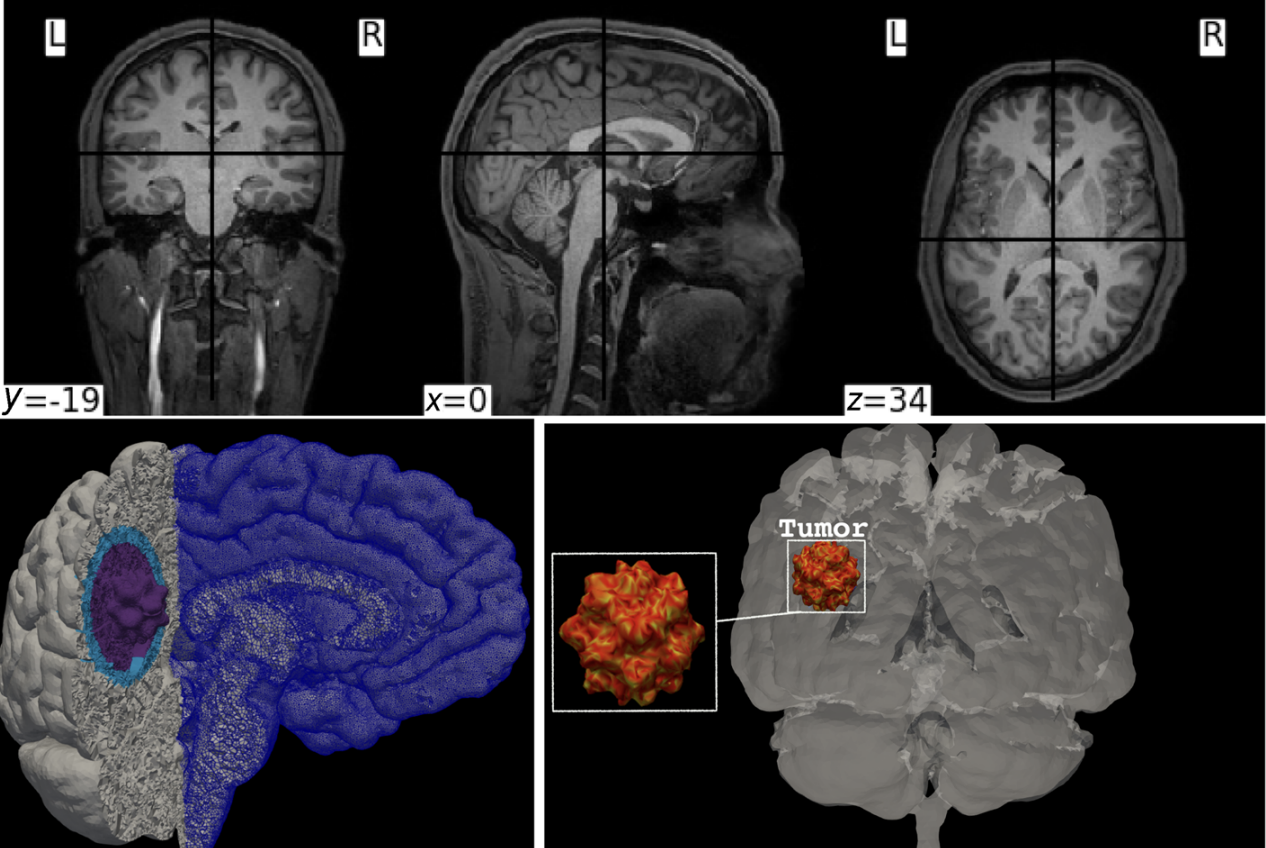
Upper panel: sample of the MRI images used to create the mesh for the cerebrum, the cerebellum, and the brainstem. Lower panel: illustration of the mesh and tumor structure. The total number of hexahedral elements is ≈ 3.289 9 × 106, and the number of DOFs is ≈ 18.949 6 × 106
By accurately capturing how the virus spreads and interacts with tumor cells and the immune system, our methods facilitate a deeper understanding of the treatment's effectiveness under various conditions. We observed that the oncolytic virotherapy successfully reduced the size of the tumor until it completely disappeared. These results suggest that the use of oncolytic M1 virotherapy may be an effective treatment for cancer patients, potentially eliminating the need for additional treatments such as chemo-radiation or surgery. The ability to simulate virotherapy dynamics can lead to improved treatment protocols. By predicting how the virus behaves in different tumor microenvironments, clinicians can tailor therapies to maximize efficacy while minimizing side effects.

Response of the tumor to the oncolytic M1 virotherapy at t = 0, t = 32.67, and t = 247.96
Broad Applicability and Future Directions
The simulation of epidemic spread, and the modeling of virotherapy illustrate our research's broad applicability and potential impact. By enhancing the stability and accuracy of numerical methods for reaction-diffusion equations, we provide valuable tools for understanding and combating some of the most pressing challenges in epidemic and cancer treatment.
We aim to refine our methods and explore their applicability to a broader range of reaction-diffusion systems. We aim to continue bridging the gap between mathematical theory and practical application.






Please sign in or register for FREE
If you are a registered user on Research Communities by Springer Nature, please sign in