The individual objects that make up our universe have an inevitable interaction with the environment. The reversible process is an ideal process in which the object can be treated with complete isolation from the environment. In reality, no process is absolutely reversible, and no system can operate in a completely isolated environment. Irreversibility is the most natural characteristic of all phenomena and a natural law. Since every phenomenon is reversible, it’s of great interest to investigate the physical mechanism of the irreversibility and to answer what creates it.

Obviously, we cannot create an environment that can entirely eliminate the influence of gravitational field. An object occupies a position and takes up a certain amount of time to generate the space-time fabric in the universe, and the gravitational force must have always act on it. The position that the object takes depends on the gravitational field, which in turn depends on the position of the object. The object at different positions has different quantized states in a gravitation field and thus, its mass related to its total internal energy is different at different energy states. The situation can become quite complicated because the object always moves from one place to another. To do that some work will be supplied against the gravitational force. In order to tie the gravitational field to the irreversibility, we here make the crucial connections among the theory of relativity, quantum physics, energy conservation and thermodynamics. The energy of the universe is always constant and the law of energy conservation works. We follow these rules to begin our analysis.

We start at position A to move an object to another position B, and then we move it back to position A in a gravitational field. The gravitational force must always have an effect on it under any circumstances, and the object at positions A and B has different quantized states. If the principle of energy conservation works, the work done during the process from position A to position B is not symmetrical for that done during the return trip from position B to position A. We have had to do an additional work against the gravitational force, which may be written mathematically in this way

m is the mass of the object, which is related to its total internal energy E by m=E/c² , c is the velocity of light, g is the free fall acceleration and H is the height in a gravitational field.

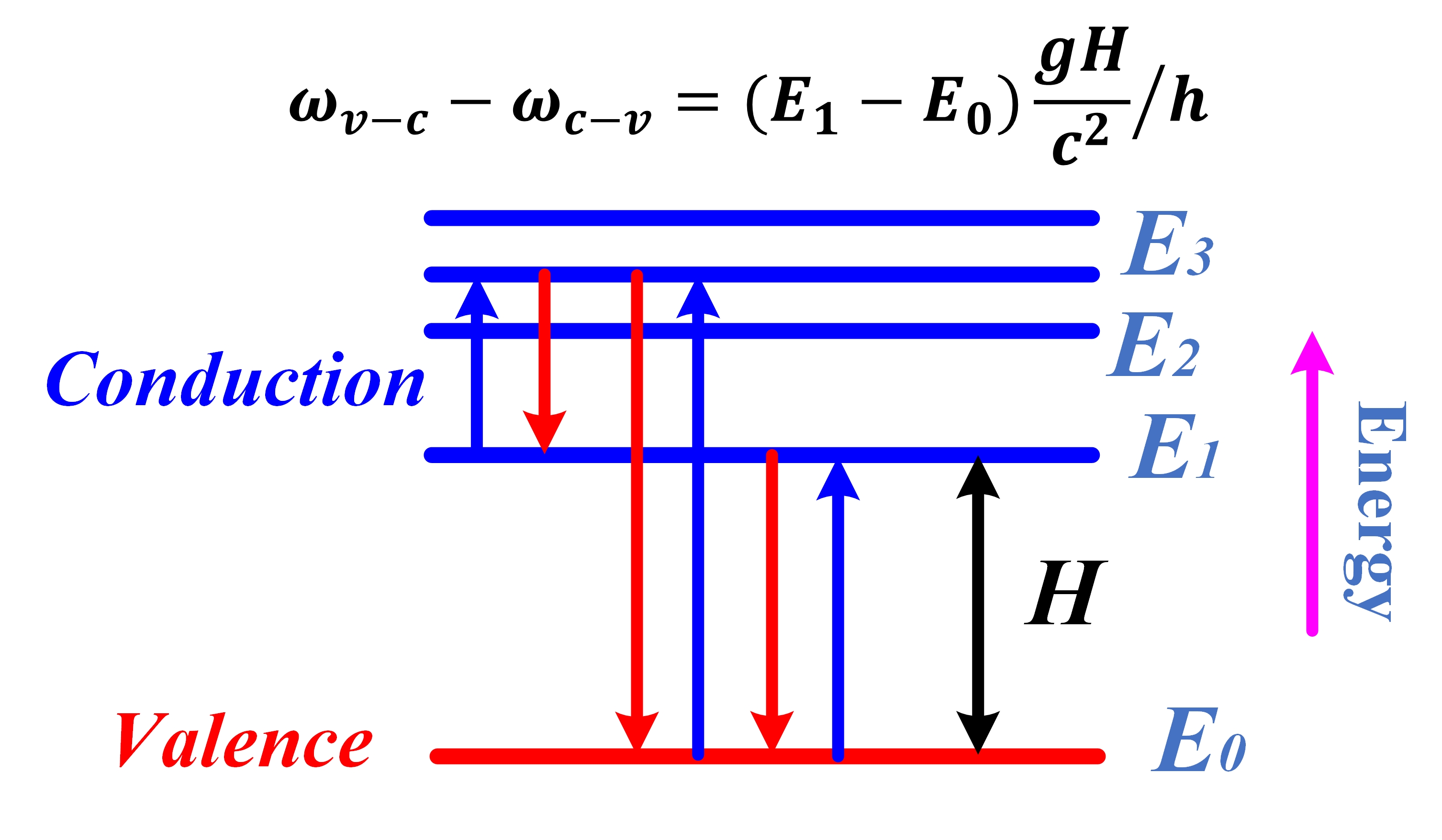
Figure 1 Energy diagram for possible transitions

We first think of the transitions from different conduction bands to the valence band in a quantum well (QW) diode in a gravitational field, for example, from energy state E₁ to energy state E₀, as show in Fig. 1. This transition happens by emitting light with a frequency of  ω_c-v. According to Planck’s formula, the energy of a photon related to its frequency will be given by  hω_c-v, h is a fundamental physical constant named the Planck constant. During the return trip, a photon with frequency  is absorbed to achieve the transition from energy state E₀ to energy state E₁. The energy of this photon is hω_v-c . Since the transition occurs in a gravitational field, a falling distance H exists from energy state E₁ to energy state E₀. Therefore, the mass will be given by  m₁=E₁/c²at the energy state E₁ and  m₀=E₀/c² at the energy state E₀, respectively. As a result, for a stable free fall acceleration g, the additional work should be done as

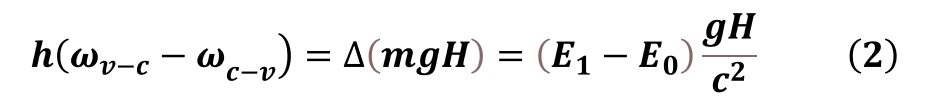
 Because the height H is not less than zero and energy state E₁ is higher than energy state E₀, we have

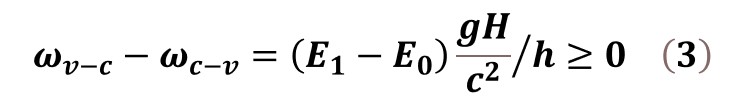
The frequency  is higher than the frequency  in the gravitational field, suggesting that the QW diode can only detect and modulate higher-energy photons than those emitted by itself. The heights H are normally very small, and consequently, the frequency differences between  and  are small.

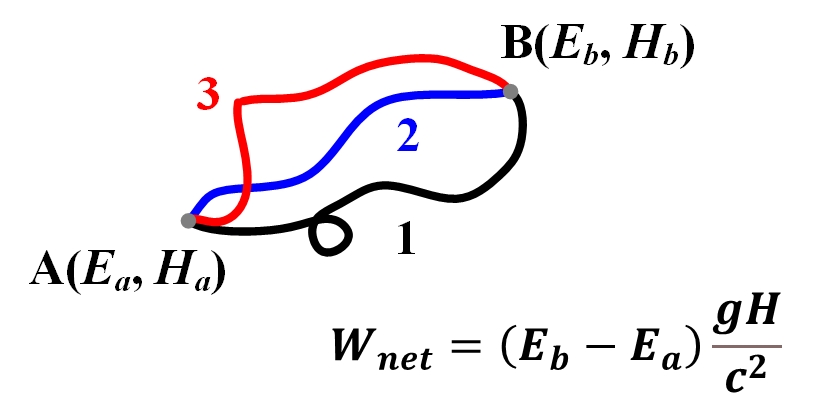
Figure 2 Possible paths between two points in a gravitational field

Proceeding in this way, we consider an object which is moved from position A to position B and brought back to position A along the same path in a gravitational field, as shown in Fig. 2. Both position A and position B are separated by the height H in this gravitational field with the free fall acceleration g. The object has a total internal energy E_b at position B and E_a at position A, respectively, in which E_b is not less than E_a. So, we have done a net amount of work against the gravitational force, which is equal to

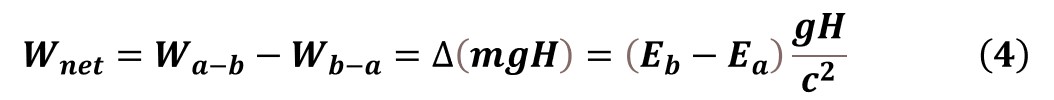
Because the height H is not less than zero and E_b is not less than E_a, we have

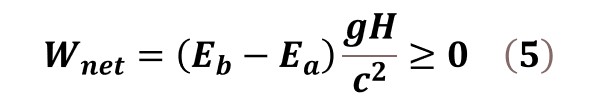
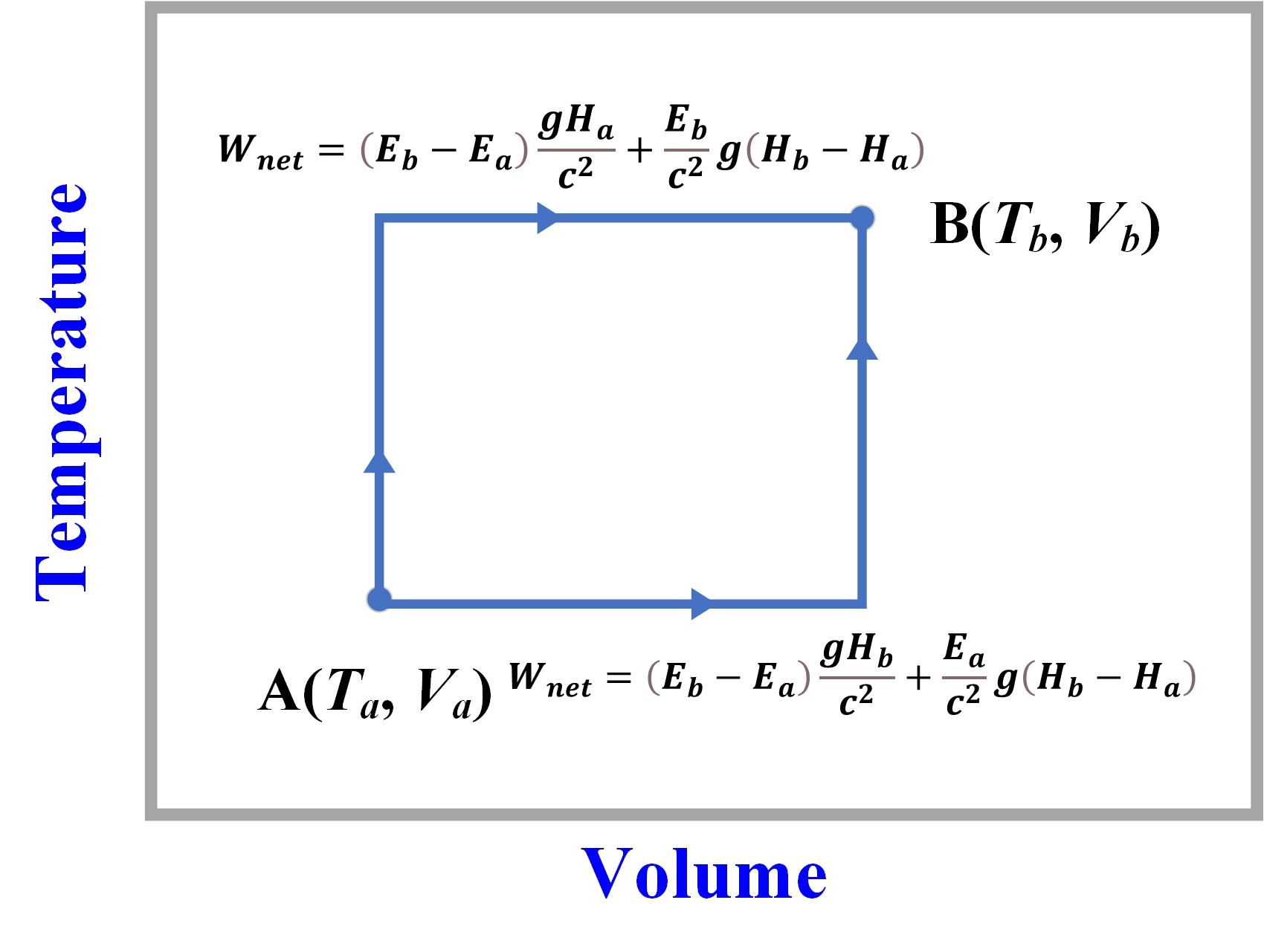
Figure 3 Change in net work in an irreversible process

In thermodynamics, we use the mean molecular kinetic energy as the definition of the temperature T. Suppose that a system operates from condition A(T_a, V_a) to condition B(T_b, V_b), changing energy states A(E_a, H_a) to B(E_b, H_b) in a gravitational field. For simple, E_b is not less than E_a, and H_b is not less than H_a. When the system goes from B(E_b, H_b) to A(E_a, H_a) and returns back from A(E_a, H_a) to B(E_b, H_b), some additional work will be done. Since  and  are equal to  and , respectively, according to the equivalence principle, the net amount of work done is given by

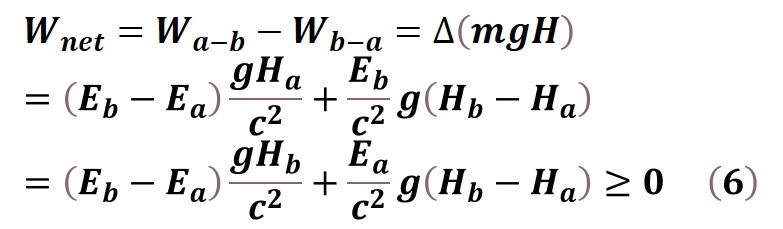
For a stable temperature T_a=T_b, E_a is equal to E_b, the net work done depends on the change of the volume, and will be given by

For a stable volume V_a=V_b, H_a is equal to H_b, the net work done depends on the change of the temperature, and will be given by

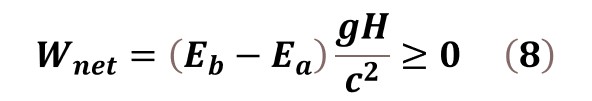
Our postulations are based on the law of energy conservation and the equivalence principle: (1) The individual objects cannot be completely isolated from the environment in reality, and the gravitational force must always act on them under any circumstances; (2) The objects at different positions have different quantized states in a gravitation field and their masses in turn depends on their energy states. (3) the amount of work done against the gravitational force is different when the object moves from one place to another and goes back to the starting position. The theory of relativity, quantum physics and energy conservation all fit together to connect the gravitational field with the irreversibility. We can conclude that the gravitational effect creates the irreversibility.